前言:本文是本人的一些浅薄见解,受水平限制,如有不当或者缺漏之处,还望各位内行指正补充。
一位老司机,名字叫罗尔,来到秋名山,喇叭嘀嘀嘀。
罗尔发车了。
秋名山重峦叠嶂,九曲回肠,就即便是罗尔这样的老司机,开起来也是心惊胆战,不过凭借着逆天般的车技,他还是到了终点。
望着一路上坡下坡,忽高忽低,他突然冒出来一个奇怪的念头:“起点和终点是等高的,诶?好像无论我怎么上坡下坡,总有那么一个时候,我和起点终点都等高啊!而且,在最高和最低的地方,车身是平行于地平线的。”他很惊讶,但是很快就想明白了:“嗯,我这是汽车,不是潜地机,也不是火箭,而起点和终点又是等高的,要在这路上走,必须是有升有降,才能到终点,而且最高的,最低的地方,车身确实很平。”
罗尔一脚油门,继续往前狂飙。
很不幸,他遇到了两段很奇怪的道路。
一段路是一路上坡,结果在坡顶路消失了,取而代之的是下方很低的地方的一段路,“奶奶的,这路不连续也不给个标识啊,坑死人了。”罗尔的车划过一道完美的抛物线狠狠的拍在了地上。
“呸!这破路,怎么断开了。”车子翻了几个滚,总算是正过来了,罗尔骂骂咧咧的继续开车。
好景不长,前面又是一段及其诡异的路,上下坡的地方尖的像一把刀,可是此时别无选择,罗尔一咬牙,一脚油门踩了下去,车子在“尖刀”上上上下下,等到出了秋名山的时候,他的车地盘已经被扎了n个眼儿了。
罗尔懊恼的抱怨:“垃圾秋名山,老子再也不来飙车了,哎哟喂我的大奔哟!”
二号老司机,绰号拉格朗,一脚油门踩,咔嚓撞断树。
拉格朗日并不害怕,他相信自己的技术,一脚油门,车速很快提到了200码。
果然是车神级的人物,拉格朗日开的比罗尔稳的多,他放着摇滚开着车,好不惬意。突然,他也意识到了一个问题:“无论自己怎么加速减速,车速在180-220之间来回变动,总有那么一个时刻,他的车速等于这段路自己跑的平均速度。”他仔细想了想,没错,就是这样,平均速度嘛,终归是介于最低和最高时速之间的,从低速加到高速,从高速减到低速,都要经过这个点,哪怕只有一瞬间。
一个失神,他没控制好方向,车子狠狠的撞在了树上,树断了。拉格朗日的脑袋狠狠的怼在了方向盘上,他晕头转向的念叨着:“嗬,这次不行了,撞这一下子,找不到那个点喽!速度变得太快了,瞬间就归零了。”
三号老司机,名字叫柯西,车稳速度高,真是太流弊。
柯西开着车经过,嘲讽到:“真菜,让本座给你演示演示。”
柯西是个新晋车神,可他自己似乎不喜欢这个称号,自封车魔,不过不得不说,他的车技也是非常棒的。
他非常顺利的到达了终点,在夕阳中抽起了雪茄。
但是他有个怪癖,喜欢查看行车记录仪,他一边抽烟,一边看记录仪,还顺手把拉格朗日和罗尔的记录仪要了过来。
看着看着,他的眉头紧皱,似乎发现了什么不得了的事情。
他的脑海里迅速闪过一个念头:“看了看三辆车的数据记录,这也太妙了,在我选定的同样时常的两段路上,任意两辆车的平均速度有那么一个比值,而两辆车的瞬时速度之比,至少有那么一个等于这个值。不过,包含拉格朗日撞树的那一段过程找不到这个点,包含罗尔飞跃‘断崖’的那一段儿过程也找不到这样的点。”
柯西满意的晃了晃脑袋,拿着小本本记录下来这个惊人的发现。
诠释:
罗尔遇到的第一段路,就是正常的连续可导函数,斜率和函数值均未发生突变。
第二段路则是断崖一样的,函数值在某个时间点突然改变(高度突然变低),属于不连续函数,于是他就翻车了。
第三段路是尖刀一样了,把罗尔的车扎的满目疮痍。这就是不可导函数了(斜率突变),行驶的轨迹突然改变,好,这下也翻车了。
这就是传说中的罗尔定理,在一段起点与终点函数值相等的函数曲线上,至少有一点的函数值和起点终点相同,而且至少有一点的斜率是0,但是,只适用于连续可导函数(在给定区间内)。
拉格朗日遇到的第一段路,开的很稳,也是正常的连续可导函数。
但是第二段路就惨了,他不小心撞到了树,导致速度骤降为0,一瞬间,斜率改变了,函数变成了不可导函数,他也“翻车了”
这是拉格朗日中值定理,即在一段函数曲线上,至少有那么一点,该点的斜率等于起终点连线的斜率(就是文中的瞬时速度和平均速度),但是仍然只限于连续可导函数,否则还是不成立。
柯西显然精明的多,他没有亲自去试那些诡异的道路,而是调出了记录仪。
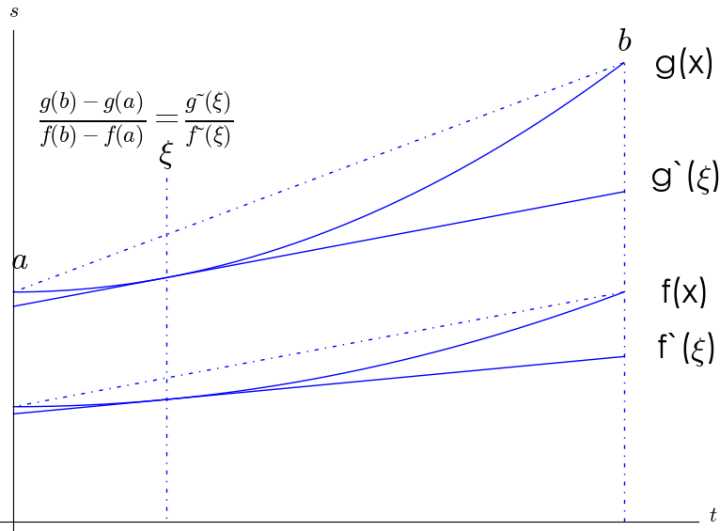
他发现的,就是柯西中值定理了,对于两个连续可导函数,在给定区间,至少有那么两点,斜率之比等于两段函数端点连线斜率之比。当然,如果任意有一个或者两个函数都不可导/不连续,就足以搞砸这一切。