在学习各种优化方法之前,我们需要先从简单的一维优化问题开始,即只有单一变量的优化问题,解决这类问题的方法可称为一维搜索技术,亦可称为线性所搜(Line Search)。一维搜索技术既可以独立的应用于求解单变量的优化问题,同时又是求解多变量优化问题的常用手段。
在大多数多变量函数的最优化中,迭代格式为:
其中最为关键的就是往哪走的搜索方向和走多少的步长因子,如果确定了搜索方向,那么求解步长因子的问题就是一维优化问题,不妨设:
这样凡从出发,沿搜索方向,确定步长因子,使得(该系列文章涉及的优化方法以及步骤均默认为求极小值)的问题就是关于步长因子的一维搜索问题。其主要结构可作如下概括:首先确定包含问题最优解的搜索区间,然后采用某种分割技术或者插值方法缩小这个区间,进行搜索求解。
一维搜索方法可以分为两大类,即精确搜索和非精确搜索。精确搜索,顾名思义就是求的极小值,此时得到的称为最优步长因子。如果选取的使得在可接受的范围内,这种情况就称为非精确的搜索。由于实际计算中,一般做不到精确的一维搜索,实际上也没有必要做到这一点,因为精确的一维搜索需要付出较高的代价,对加速收敛作用不大,因此花费计算量较少的不精确的一维搜索技术方法受到更为广泛的重视和欢迎。 但了解精确的一维搜索技术对于非精确的技术有帮助,所以本系列最开始依然先从精确的一维搜索技术展开。
精确的一维搜索技术
通常根据算法中有无使用导数,将精确的一维搜索技术分为两类,即无导数信息的试探法,包括二分法、黄金分割法、Fibonacci法、进退法等;有导数信息的插值法,包含二次插值法、牛顿法等。
高低高(单峰)区间定位(initially bracketing a minmum)
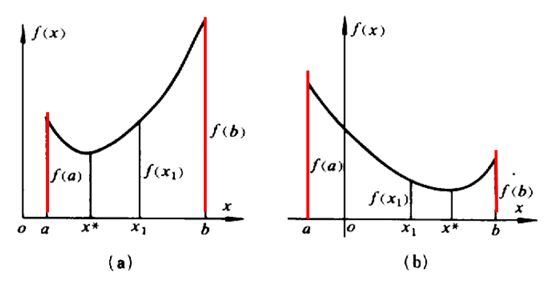
对于求根问题,通过两点相乘为负即可确定一个区间(连续函数)。那么对于求解一维函数的局部极小值得问题,可以通过三点信息获得(a triplet of points),即如果,使得均小于和,且函数连续,那之间就存在一个局部极小值,如下图所示:
高低高区间的确定,最为常见的方法是进退法。
进退法的思想是先试探、再判断是进还是退,直到得到,且均小于和情况,则可确定区间。
Algorithm 1 进退法
function [a,b,c] = bracketAdvanceBack(func,x0,h0,plotFlag)
if nargin < 4
plotFlag = 0;
end
if nargin <3
h0 = 0.01;
end
if nargin <2
x0 = 0;
end
if plotFlag == 1
figH = figure();
k = 0;
end
x1 = x0;
h = h0;
x2 = x1 + h;
fx1 = func(x1);
fx2 = func(x2);
%试探
if fx2>=fx1 %说明极小点位于x1的左方,后退搜索,即将步长设定 为负,x1和x2交换
h = -h0;
swap(x1,x2);
swap(fx1,fx2);
end
at = x0;
bt = x2;
iterNum = 1000;
while(iterNum)
h = 2*h;
x3 = x2 + h;
fx3 = func(x3);
ct = x3;
if plotFlag == 1
% pause(1);
plot(x0-300*h0:h0:x0+300*h0,func(x0-300*h0:h0:x0+300*h0),'-b',x1...
,func(x1),'or',x2,func(x2),'og',x3,func(x3),'ob');
print(figH,'-dpng',strcat('plotIm_',num2str(k)));
k = k+1;
end
if fx3>fx2
at = x1;
bt = x2;
ct = x3;
break;
else
x1 = x2;
x2 = x3;
fx2 = fx3;
end
iterNum = iterNum - 1;
end
a = min(at,ct);
b = bt;
c = max(at,ct);
end
function [x,y]=swap(x,y)
t = x;
x = y;
y = t;
end
注:本系列相关matlab代码,对输入的部分异常情况没有进行处理
Numerical recipes 10.1节中提供一种利用三点构建的抛物线极小点进行高低高区间的搜索,这种方法相比传统的进退法在同样的初始条件下,能更快的找到高低高区间,算法如下:
Algorithm 2 抛物线法
function [a,b,c] = bracket(func,a,b,plotFlag,step,steplimit)
if nargin < 6
steplimit = 10;
end
if nargin < 5
step = 1.618034;
end
if nargin < 4
plotFlag = 0;
end
if nargin <3
b= 1;
end
if nargin <2
a = 0;
end
if abs(a-b) > 1
warning('the initial interval is too lager and the result may be unsatisfactory!')
end
if a>b
[a,b]=swap(a,b);
end
abInt = (b-a)/10;
abInt = min(abInt,0.1);
GOLD = step;
GLIMIT = steplimit;
ax = a;
bx = b;
fax = func(ax);
fbx = func(bx);
if fbx>fax
[fbx,fax]=swap(fbx,fax);
[bx,ax]=swap(bx,ax);
abInt = -abInt;
end
cx = bx + GOLD*(bx-ax);
fcx = func(cx);
if plotFlag == 1
figure, plot(ax:abInt:cx,func(ax:abInt:cx),'-b',ax,func(ax),'or',bx,func(bx),'og',cx,func(cx),'ob');
end
while fbx>fcx
r = (bx-ax)*(fbx-fcx);
q = (bx-cx)*(fbx-fax);
ux = bx -((bx-cx)*q-(bx-ax)*r)/(2.0*MySignFunc(max(abs(q-r),eps),q-r));%三点构建抛物线的极值点;
uxlim = bx + GLIMIT*(cx-bx);
if (bx-ux)*(ux-cx) > 0 %如果u在bx和cx之间
fux = func(ux);
if fuxfbx %我们就得到一个高低高区间 在 ax bx ux
%ax = ax;
%bx = bx;
cx = ux;
break;
end
end
ux = cx + GOLD*(cx-bx); %如果上面两个情况都不满足,就在cx的基础上扩大 ux
elseif (cx-ux)*(ux-uxlim)>0 %如果ux在cx和uxlim之间
fux = func(ux);
if fux=0.0 %如果uxlim在ux 和 cx 之间
ux = uxlim;
else
ux = ux + GOLD*(cx-bx);
end
ax = bx;
bx = cx;
cx = ux;
fax = func(ax);
fbx = func(bx);
fcx = func(cx);
if plotFlag == 1
pause(1);
plot(ax:abInt:cx,func(ax:abInt:cx),'-b',ax,func(ax),'or',bx,func(bx),'og',cx,func(cx),'ob');
end
end
abc = sort([ax,bx,cx]);
a = abc(1);
b = abc(2);
c = abc(3);
end
function [x,y]=swap(x,y)
t = x;
x = y;
y = t;
end
function a = MySignFunc(a,x)
a = abs(a);
if x<0
a = -a;
end
end
二分法
严苛点,假设函数在区间存在极小值,且
(1)若,则,说明极小值在;
(2)若,则,说明极小值在;
则称为在区间上是单谷函数。在搜索区间时,我们找到的高低高区间往往是单谷函数,确保单谷函数后,就有一系列的分割式的方法进行精确的一维搜索极值的方法,其中最简单就是二分法,类似求函数过零点的方法,具体如下:
Algorithm 3 二分法
function x_min = BiSection(func,a,b,c,toll,plotFlag)
if nargin < 6
plotFlag = 0;
end
if nargin < 5
toll = 10^(-8);
end
if (a-b)*(b-c)<=0
x_min = 0;
disp('ab>c is needed!');
return ;
end
if (a>c)
t=a;
a=c;
c=t;
end
x_mid = (a+c)/2;
if plotFlag == 1
figH = figure();
acInt = (c-a)/100;
plot(a:acInt:c,func(a:acInt:c),'-b',x_mid,func(x_mid),'-ro',a,func(a),'-*r',b,...
func(b),'-*g',c,func(c),'-*b');
hold on;
end
while abs(a-c)>2*toll
if x_mid == b
x_mid = (a+b)/2;
end
if x_mid>b
if func(x_mid) > func(b) %极小值在b的右端
c = x_mid;
else %极小值在x_mid的左端
a = b;
b = x_mid;
end
else
if func(x_mid) > func(b) %极小值在b的右端
a = x_mid;
else %极小值在x_mid的左端
c = b;
b = x_mid;
end
end
x_mid = (a+c)/2;
if plotFlag == 1
pause(0.15);
plot(x_mid,func(x_mid),'-ro');
end
end
hold off;
x_min = (b+x_mid)/2;
二分法是一种最简单的分割方法,每次迭代都将搜索区间缩短一半,故二分法的收敛速度是 线性的,收敛比是0.5,收敛速度较慢。其优势是每一步迭代的计算量相对较少,逻辑简单,而且总能收敛到一个局部极小点。
Fibonacci 分数法
兔子生兔子问题大家很熟悉,其就是典型的Fibonacci数列,数学定义为:
数列称为斐波那契(Fibonacci)数列,称为第n个Fibonacci数,相邻两个Fibonacci数之比称为Fibonacci分数。从二分法中,可以得出下面的结论:
只要在区间内任取两个不同点,并算出他们的函数值加以比较,就可以把搜索区间缩小为或 ,因为缩小后的区间仍包含极小点。要进一步缩小搜索区间,只需在缩小后的区间内再取一点,并与 或比较函数值大小。按照这样的步骤迭代进行,随着计算函数值次数的 增加,区间越来越小,从而越接近极小点。
这是分割类方法的通用思想,即通过不断的缩小区间达到极值点。Fibonacci 分数法是利用这一思想,只是搜索区间的长度不再是二分法的0.5,而是采用Fibonacci数列。
Algorithm 4 Fibonacci 分数法
function x_min = FibonacciSection(func,a,b,toll,plotFlag)
%确保[a,b]为单峰区间
if nargin < 5
plotFlag = 0;
end
if nargin < 4
toll = 10^(-8);
end
if (a>b)
[a,b]=swap(a,b);
end
%step 1 初始化数据
Ln = (b-a)^2/toll;
F(1) = 1;
F(2) = 1;
n = 2;
%step 2 求Fibonacci数列
while F(n)Fibonacci分数法可以证明是最优策略。相对二分法Fibonacci分数法收敛快,然而开始需要确定迭代次数,计算Fibonacci数列,每步取点繁琐,各步缩短率不同。为此,引入黄金分割法。
黄金分割法
黄金分割法内分点的原则是:对称且每次区间缩短率相等。对称性来自Fibonacci分数法,固定缩短率也是改进Fibonacci分数发的不足,可见黄金分割法和Fibonacci分数法是有联系。的确,可以证明Fibonacci的缩短率在极限情况下就是黄金分割法的缩短率,0.618。有兴趣的读者可以查找相关资料。
在搜索区间内适当插入两点,,且在区间内对称位置,计算其函数值,
(1)若,则极小点必在区间内,令,新区间为;
(2)若,则极小点必在区间内,令,新区间为。
经过函数值比较 ,区间缩短一次。新区间只保留中的一个。
设原区间长度为,保留区间长度为,区间缩短率为。进行第二次缩短时,新点,设,则新区间为。设区间缩短率为。为了保持相同的区间缩短率,应有:
由此可得:割法又称为0.618法。黄金分割法是一种等比例缩短区间的直接搜索方法,适用于[a,b]区间上的任何单谷函数求解极小值问题。对函数除要求单谷外不作其他任何要求,甚至可以不连续,因此适应面广。
Algorithm 5 黄金分割法
function x_min = GoldSection(func,a,b,toll,plotFlag)
%确保[a,b]为单峰区间
if nargin < 5
plotFlag = 0;
end
if nargin < 4
toll = 10^(-8);
end
if (a>b)
[a,b]=swap(a,b);
end
GOLD = (sqrt(5)-1)/2;
%step 1 初始化x1 x2
x1 = a+(1-GOLD)*(b-a);
x2 = a+GOLD*(b-a);
fx1 = func(x1);
fx2 = func(x2);
if plotFlag == 1
figH = figure();
abInt = (b-a)/100;
xx = a:abInt:b;
for i = 1:1:length(xx)
yy(i) = func(xx(i));
end
plot(xx,yy,'-b',a,func(a),'-*r',b,func(b),'-*g');
hold on;
end
%step 2 ,迭代缩短区间
while abs(a-b)>toll
if fx1黄金分割法和Fibonacci分数法也是线性收敛,收敛比率约0.618
二次插值法
二分法、Fibonacci分数法以及黄金分割法都属于试探法,即试验点的位置是由某种给定的规则确定的,并没有考虑数值的分布,仅仅利用试验点函数值进行大小的比较;插值法试验点的位置是按照函数近似分布的极小点确定的,即插值法需要利用函数值本身或其导数信息,所以当函数具有较好的解析性质时,插值法比试探法效果更好。
利用原目标函数上的三个插值点,构成一个二次插值多项式,用该多项式的最优解作为原函数最优解的近似解,逐步逼近原目标函数的极小点,称为二次插值方法或近似抛物线法。简单流程如下图所示:
Algorithm 6 二次插值法
function x_min = ParabolicInterpolationSection(func,a,b,toll,plotFlag)
%确保[a,b]为单峰区间,且连续
if nargin < 5
plotFlag = 0;
end
if nargin < 4
toll = 10^(-8);
end
if (a>b)
[a,b]=swap(a,b);
end
if plotFlag == 1
figH = figure();
abInt = (b-a)/100;
plot(a:abInt:b,func(a:abInt:b),'-b',a,func(a),'-*r',b,func(b),'-*g');
hold on;
end
%step 1 初始化
x1 = (a+b)/2;
%step 2 迭代缩短区间
while abs(a-b) > toll
fa = func(a);
fx1 = func(x1);
fb = func(b);
r = (x1-a)*(fx1-fb);
q = (x1-b)*(fx1-fa);
C1 = (x1-a)*r-(x1-b)*q;
C2 = r-q;
if C2 == 0 %说明三点共线,对于单峰情况,三点共点了,退出
break;
end
x2 = x1 - 1/2*C1/C2; %计算抛物线的极值点
if (x2-a)*(b-x2)<=0 %极值点不在区间内(两点共点)
break;
end
fx2 = func(x2);
if x2>x1
if fx1=fx2,则说明极小值在x1 b区间内
a = x1;
fa = fx1;
x1 = x2;
fx1 = fx2;
end
else
if fx1=fx2,则说明极小值在a x1区间内
b = x1;
fb = fx1;
x1 = x2;
fx1 = fx2;
end
end
if plotFlag == 1
pause(0.15);
plot(a,fa,'-*r',b,fb,'-*g');
end
end
if plotFlag == 1
hold off;
end
x_min = (a+b)/2;
end
function [a,b]=swap(a,b)
t=a;
a=b;
b=t;
end
三点二次插值法并没有直接用到函数的导数信息,且相同迭代次数下,可以得到更精确的结果,其收敛比率为1.3,在有解析表达式,函数连续情况下,是很实用的。但抛物线法也有不收敛的情况[1],为此Brent做了改进,见后文Brent's Method。
插值法还有很多,比如两点二次插值,三次插值,牛顿法,有理插值法等,这些方法需要用到导数信息。下面我们介绍牛顿法,即一点二次插值法。其他方法如果读者有兴趣了解,可自行从网上检索相关算法。
牛顿法
当原函数存在一阶二阶连续可导时,可以采用牛顿法进行一维搜索,收敛速度快,具有局部二阶收敛速度。牛顿法的思想是用二次函数逐点近似原目标函数,以二次函数的极小点来近似原目标函数的极小点,用切线代替狐仙逐渐逼近导数函数的根。可以理解为当目标函数有一阶连续导数,且二阶导数大于零时,函数的极小值点应该满足极值点存在的必要条件,即导数为0,所以求函数的极小值点也就是求解函数一阶导数为0的根。
过点的切线方程为:
与轴的交点为:
推广到k步得到迭代公式:
此外迭代公式也可以由Taylor公式展开得到:
在附近用二次函数来逼近原目标函数,故在点用Taylor公式展开,保留到二次项:
令,也可以得到上面的迭代公式。
Algorithm 7 牛顿法(一维线性搜索)
function x_min = NewtonLinSrch(func,dfunc,ddfunc,a,b,toll,plotFlag)
%func 一阶二阶连续可导,且二阶导数大于0
if nargin < 7
plotFlag = 0;
end
if nargin < 6
toll = 10^(-8);
end
if (a>b)
[a,b]=swap(a,b);
end
x1 = (a+b)/2;
if plotFlag == 1
figH = figure();
abInt = (b-a)/100;
plot(a:abInt:b,func(a:abInt:b),x1,func(x1),'-ro');
hold on;
end
while abs(dfunc(x1))>toll&&ddfunc(x1)>0
x1 = x1 - dfunc(x1)/ddfunc(x1);
if (x1-a)*(b-x1)<=0
break; %如果x1超界,说明一阶导数或者二阶导数不满足使用牛顿法的条件
end
if plotFlag == 1
pause(0.15);
plot(x1,func(x1),'-ro');
end
end
x_min = x1;
end
function [a,b]=swap(a,b)
t=a;
a=b;
b=t;
end
Brent's Method
以上精确的一维搜索方法各有优缺点,Brent为了在所有特殊情况下都能较好的适用,提出了Brent's Method[1]。该方法也被收录在Matlab的优化库中,即fminbnd函数。该方法结合了二次插值方法和黄金分割法,它在任何特殊的情况中,都保持6个函数点,即。其中最小值在和之间,是迭代一次找的最小值对应的函数点,是次小点,是前一次迭代点,是当前迭代的函数点。可以通过阅读小面的matlab代码来理清Brent's Method的逻辑。其核心思想是大区间下采用二次插值法,小区间的时候采用黄金分割法,来避免二次插值法在小区间陷入循环的弊病。几点需要注意[1]:
1、二次插值使用三点;
2、插值出来的抛物线极值点一定在区间内;
3、 的移动步长不大于上一次的一半([1]中说这样做可以使得插值计算的这一步收敛在比较好的点上,避免nonconvergent limit circle)
Algorithm 8 Brent's Method
function x_min = BrentMethod(func,a,b,c,tol,iterNum,plotFlag)
%Brent's Method fminbnd
if nargin < 7
plotFlag = 0;
end
if nargin < 6
iterNum = 100;
end
if nargin < 5
tol = 10^(-8);
end
if (a-b)*(b-c)<=0
x_min = 0;
disp('ab>c is needed!');
return ;
end
if (a>c)
b = a;
a = c;
else
b = c;
end
if plotFlag == 1
figH = figure();
abInt = (b-a)/100;
plot(a:abInt:b,func(a:abInt:b));
hold on;
end
GOLD = 1 - (sqrt(5)-1)/2.0;
x = b;
w = b;
v = b;
fw = func(w);
fx = fw;
fv = fw;
e = 0;
d = 0;
for i=1:1:iterNum
xm = (a+b)/2.0;
tol1 = tol*abs(x)+eps;
tol2 = 2*tol1;
if plotFlag == 1
pause(0.15);
plot(x,fx,'-ro');
end
if abs(x-xm) <= (tol2-0.5*(b-a))
x_min = x;
return;
end
if abs(e)>tol1 %这种情况下是用二次插值法
r = (x-w)*(fx-fv);
q = (x-v)*(fx-fw);
p = (x-v)*q - (x-w)*r;
q = 2.0*(q-r);
if q>0
p = -p;
end
q = abs(q);
etemp = e;
e = d;
if abs(p) >= abs(0.5*q*etemp)||p<=q*(a-x)||p>=q*(b-x)
%采取黄金分割法得到更大的两段
if x>=xm %从a,x,b区间段中 找最大的一段,乘以GOLD作为下一次的步长
e = a-x;
else
e = b-x;
end
d = GOLD*e;%二次插值法不被接受,采用golden section
else
d = p/q;
u = x + d; %采用二次插值法
if u-a=xm
e = a-x;
else
e = b-x;
end
d = GOLD*e;%二次插值法不被接受,采用golden section
end
if abs(d) >= tol1 %步长选择tol1和d中较小的一个
u = x+d;
else
u = x+MySignFunc(tol1,d);
end
fu = func(u);
if fu<=fx %如果fu小于fx,说明下次迭代为区间不是在[a,x],就是在[x,b]
if u>=x %如果u>=x,则在[x,b],反之在[a,x]
a = x;
else
b = x;
end
v = w;w = x;x = u;
fv = fw;fw = fx;fx = fu;
else%反之,说明下次迭代区间不是[a,u],就是[u,b]
if u 参考文献
[1] Numerical Recipes, William H. Press