一、什么是拓扑排序
在图论中,拓扑排序(Topological Sorting) 是一个 有向无环图(DAG,Directed Acyclic Graph) 的所有顶点的线性序列。且该序列必须满足下面两个条件:
- 每个顶点出现且只出现一次。
- 若存在一条从顶点A到顶点B的路径,那么在序列中顶点A出现在顶点B的前面。
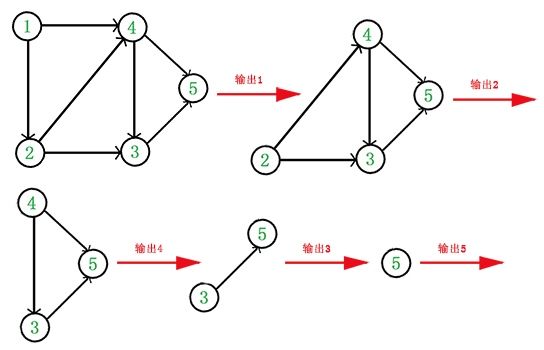
例如,下面这个图:
它是一个DAG图,那么如何写出它的拓扑顺序呢?这里说一种比较常用的方法:
- 从DAG途中选择一个没有前驱(即入度为0)的顶点并输出
- 从图中删除该顶点和所有以它为起点的有向边。
-
重复1和2直到当前DAG图为空或当前途中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环。
于是,得到拓扑排序后的结果是{1,2,4,3,5}
二、什么是C3算法
python多重继承的MRO算法选择: 经典方式、Python2.2 新式算法、Python2.3 新式算法(C3)。Python 3中只保留了最后一种,即C3算法
mro即method resolution order,主要用于在多继承时判断调的属性的路径(来自于哪个类)。mro是基于深度优先搜索算法的。在Python2.3之前是基于此算法,但从Python2.3起应用了新算法:C3算法。
C3算法的本质就是Merge,不断地把mro�()函数返回的序列进行Merge,规则如下:
如果第一个序列的第一个元素,是后续序列的第一个元素,或者不在后续序列中再次出现,则将这个元素合并到最终的方法解析顺序序列中,并从当前操作的全部序列中删除。
如果不符合,则跳过此元素,查找下一个列表的第一个元素,重复1的判断规则
C3算法的解析:
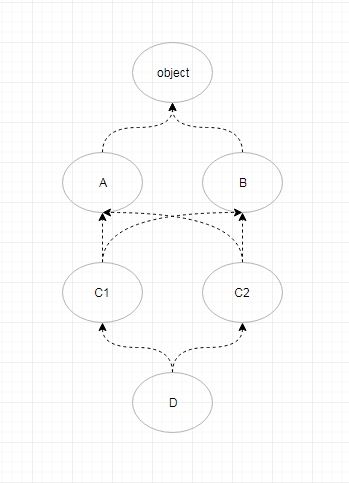
1.多继承UML图:
备注:O==object
2.python-C3算法解析:
C3 算法:MRO是一个有序列表L,在类被创建时就计算出来。
L(Child(Base1,Base2))= [ Child + merge( L(Base1), L(Base2),Base1Base2 )]
L(object)= [ object ]
L的性质:结果为列表,列表中至少有一个元素即类自己。
+: 添加到列表的末尾,即 [ A + B ] = [ A,B ]
merge:
- ① 如果列表空则结束,非空,读merge中第一个列表的表头,
- ② 查看该表头是否在merge中所有列表的表尾中。
- ②-->③ 不在,则放入最终的L中,并从merge中的所有列表中删除,然后回到①中
- ②-->④ 在,查看当前列表是否是merge中的最后一个列表
- ④-->⑤ 不是,跳过当前列表,读merge中下一个列表的表头,然后回到 ②中
- ④-->⑥ 是,异常。类定义失败。
表头: 列表的第一个元素 (列表:ABC,那么表头就是A,B和C就是表尾)
表尾: 列表中表头以外的元素集合(可以为空)
merge 简单的说即寻找合法表头(也就是不在表尾中的表头),如果所有表中都未找到合法表头则异常。
例如:
L(D) = L(D(O))
= D + merge(L(O))
= D + O
= [D,O]
L(B) = L(B(D,E))
= B + merge(L(D) , L(E))
= B + merge(DO , EO) # 第一个列表DO的表头D,其他列表比如EO的表尾都不含有D,所以可以将D提出来,即D是合法表头
= B + D + merge(O , EO) #从第一个开始表头是O,但是后面的列表EO的表尾中含有O所以O是不合法的,所以跳到下一个列表EO
= B + D + E + merge(O , O)
= [B,D,E,O]
同理:
L(C) = [C,E,F,O]
L(A(B,C)) = A + merge(L(B),L(C),BC)
= A + merge(BDEO,CEFO,BC) # B是合法表头
= A + B + merge(DEO,CEFO,C) # D是合法表头
= A + B + D + merge(EO,CEFO,C) # E不是合法表头,跳到下一个列表CEFO,此时C是合法表头
= A + B + D + C + merge(EO,EFO) # 由于第三个列表中的C被删除,为空,所以不存在第三个表,只剩下两个表;此时E是合法表头
= A + B + D + C + E + merge(O,FO) # O不是合法表头,跳到下一个列表FO,F是合法表头,
= A + B + D + C + E + F + merge(O,O) # O是合法表头
= A + B + D + C + E + F + O
= [A,B,D,C,E,F,O]
获取C3的数组列表,可以梳理清楚子类执行过程中向上执行的顺序
三、Python多重继承
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
class A(object):
def foo(self):
print('A foo')
def bar(self):
print('A bar')
class B(object):
def foo(self):
print('B foo')
def bar(self):
print('B bar')
class C1(A,B):
pass
class C2(A,B):
def bar(self):
print('C2-bar')
class D(C1,C2):
pass
if __name__ == '__main__':
print(D.__mro__)
d=D()
d.foo()
d.bar()
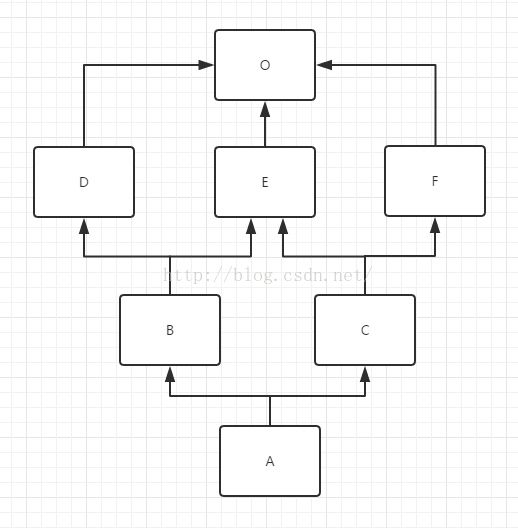
首先,我们根据上面的继承关系构成一张图,如下
- 找到入度为0的点,只有一个D,把D拿出来,把D相关的边剪掉
- 现在有两个入度为0的点(C1,C2),取最左原则,拿C1,剪掉C1相关的边,这时候的排序是{D,C1}
- 现在我们看,入度为0的点(C2),拿C2,剪掉C2相关的边,这时候排序是{D,C1,C2}
- 接着看,入度为0的点(A,B),取最左原则,拿A,剪掉A相关的边,这时候的排序是{D,C1,C2,A}
- 继续,入度为0的点只有B,拿B,剪掉B相关的边,最后只剩下object
- 所以最后的排序是{D,C1,C2,A,B,object}
我们执行上面的代码,发现print(D.mro)的结果也正是这样,而这也就是多重继承所使用的C3算法啦
(, , , , , )
A foo
C2-bar
为了进一步熟悉这个拓扑排序的方法,我们再来一张图,试试看排序结果是怎样的,它继承的内容是否如你所想
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
class A(object):
def foo(self):
print('A foo')
def bar(self):
print('A bar')
class B(object):
def foo(self):
print('B foo')
def bar(self):
print('B bar')
class C1(A):
pass
class C2(B):
def bar(self):
print('C2-bar')
class D(C1,C2):
pass
if __name__ == '__main__':
print(D.__mro__)
d=D()
d.foo()
d.bar()
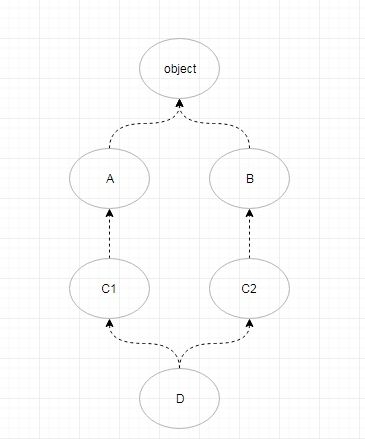
还是先根据继承关系构一个继承图
- 找到入度为0的顶点,只有一个D,拿D,剪掉D相关的边
- 得到两个入度为0的顶点(C1,C2),根据最左原则,拿C1,剪掉C1相关的边,这时候序列为{D,C1}
- 接着看,入度为0的顶点有两个(A,C1),根据最左原则,拿A,剪掉A相关的边,这时候序列为{D,C1,A}
- 接着看,入度为0的顶点为C2,拿C2,剪掉C2相关的边,这时候序列为{D,C1,A,C2}
- 继续,入度为0的顶点为B,拿B,剪掉B相关的边,最后还有一个object
- 所以最后的序列为{D,C1,A,C2,B,object}
最后,我们执行上面的代码,发现print(D.mro)的结果正如上面所计算的结果
(, , , , , )
A foo
A bar
python继承顺序遵循C3算法,只要在一个地方找到了所需的内容,就不再继续查找
参考
python 多重继承之拓扑排序
Python新式类继承的C3算法
python多重继承C3算法