欢迎参考,但 。。。。。。
不要照搬就好!
1. Abstract
There are a flood of examples about chaos, good understanding of them is very useful for us to predict some normal but interesting in our daily life.
Question 3.30
Investigate the Lyapunov exponent of the stadium billiard for several values of \alpha. You can do this qualitatively by examining the behavior for only one set of initial conditions for each value of \alpha you consider, or more quantitatively by averaging over a range of initial conditions for each value of \alpha.
Question 3.31
Study the behavior for other types of tables. One interesting possibility is a square table with a circular interior wall located either in the center, or slightly off-center. Another possibility is an elliptical table.
2. Background and Introduction
We have already considered the model of the pendulum. Maybe it is quite easy, yet they exhibit extremely rich behavior. It is thus not surprising that other sightly more complicated systems are also capable of chaotic behavior. When we think of chaotic or unpredictable behavior, an example that naturally comes to mind is the weather. While much of this effort has gone into computer modeling of Earth's atmosphere, much has also been devoted to understanding the weather problem from a more fundamental points of view.
To get an appreciation for the different kinds of behavior that can be found, and also the common threads that run through this behavior, we will consider one more chaotic model inthis homework. Here we consider the problem of a ball moving without friction on a horizontal table. We imagine that there are walls at the edges of table that reflect the ball perfectly and that there is no frictional force between the ball and the table.
We consider the Lorenz model, the Lorenz equations can be written as:
Use computer programs, we can predict its trajectory then, we plot it in 3D-space.
The main question we will talk about is the billiard problem. Except for the collisions with the walls, the motion of the billiard is quite simple. Between collisions the velocity is constant so we have:
These equations can be solved using our usual Euler algorithm. The Euler solution gives an exact description of the motion across the table. The most difficult part of the calculation is the treatment of the collisions. We can obtain the following equations:
Hence, the velocity after reflection from the wall is :
These equations are the basis of my work in this homework.
3. Body Content and Conclusion
(1) The Lorenz model
When we plot it with z and t, we cannot find any regularity. Hence, we'd better plot it in phase-space. Here, \sigma=10, b=8/3, r=25, the step of time is 0.0001.
Click the Code
-
Conclusion: When we plot it in phase space, The figure 1. gives some hints of an underlying regularity.
Though we can predict something from the phase-space plot, we would like to have more than hints. Hence, while the time-dependent behavior is unpredictable, we can predict with certainty that the system will be found somewhere on the attractor surface in phase space.
Click the Code
-
Conclusion: We see from the figure that even though the behavior is strongly chaotic, there is a very high degree of regularity in the phase-space trajectory.
(2) Question 3.30
First, we consider a quite simple model-the motion of a billiard on a square table. The billiard started at point (0.2, 0). Specific parameters are shown in my code.
Click the Code
-
Conclusion: From figure 3., we can predict this kind of motion easily.
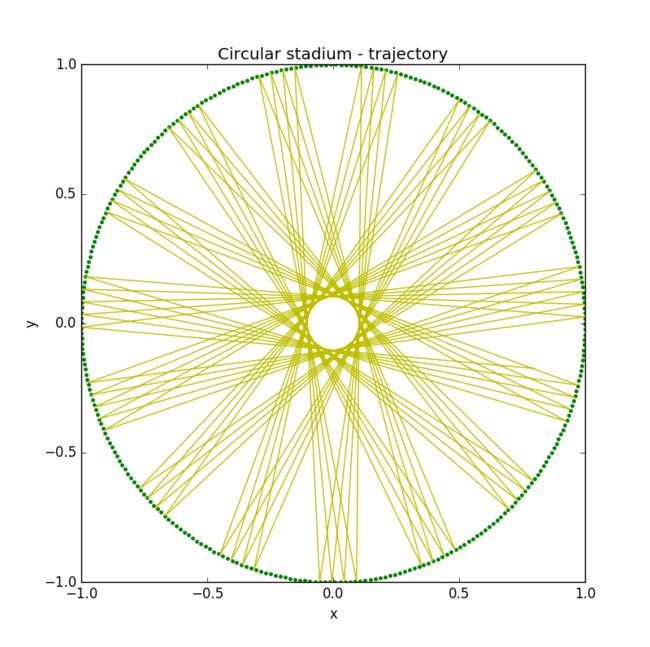
But, when we consider another table, what will change? For example, If the table is circular table, the result will be beautiful and amazing!
Click the Code
-
Conclusion: The trajectories are always highly symmetric,
By the way, I give its phase-space plot below.
Click the Code
-
Conclusion: This motion is quite regular.
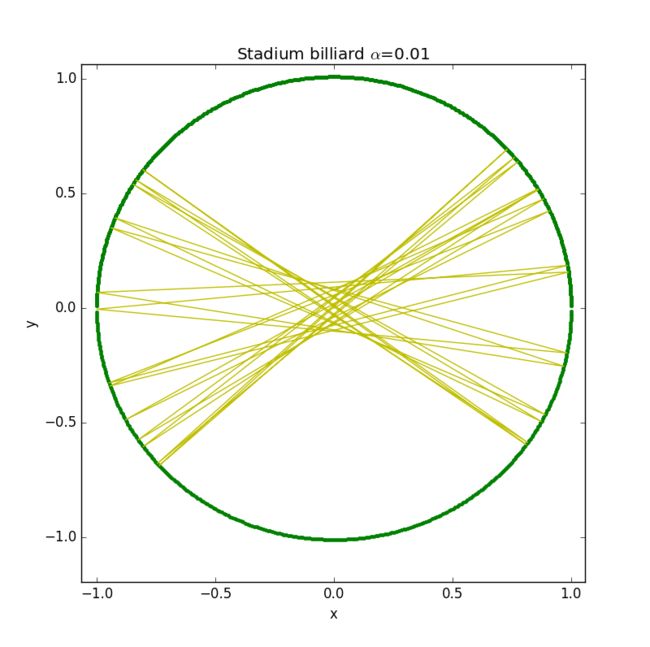
However, if we cut the table along the x axis, and pull the two semicircular halves apart (along y), a distance 2\alpha r, the trajectory will be definitely not symmetric.
Click the Code
-
Conclusion: In fact, this figure reminds us of chaotic motion.
Phase-space plots for the trajectories of \alpha=0, 0.001, 0.01, 0.1 shown in figure 7.
Click the Code
-
Conclusion: When \alpha=0, it is a nonchaotic system. However, for the \alpha is not equal to 0, it is indeed chaotic.
Now, we have enough knowdgeable to finish the first question-3.30. Here, the initial separation of the billiards was 0.00001.
Click the Code
-
As you see in figure 8. and figure 9., when \alpha is larger, the Lyapunov exponent is larger.
-
When \alpha=0, we will find that the Lyapunov exponent is zero. When \alpha=0.001, the Lyapunov exponent is much small. However, when \alpha become larger, \alpha=0.01, the Lyapunov exponent is equal to 0.05, \alpha=0.1, the Lyapunov exponent is 0.17.
-
The result told us, when \alpha is larger, the system is more chaotic.
(3) Question 3.31
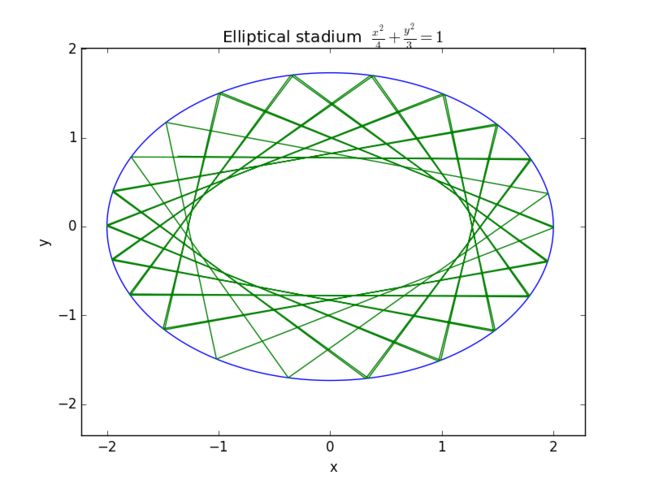
Of course, we can also obtain the trajectory of billiard in elliptical table. I give two figure here, one is situation when the billiard sets out from a focal point, the other is situation when the billiard sets out from the origin.
Click the Code
Click the Code
-
Conclusion: For an ellipse, its tracjectory is related to its starting point. For above two situations, we obtain two totally different results. And there is not point of intersection in their phase-space diagram.
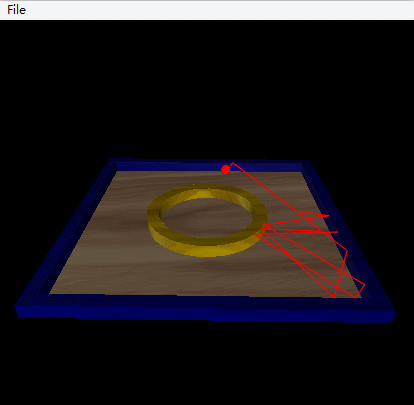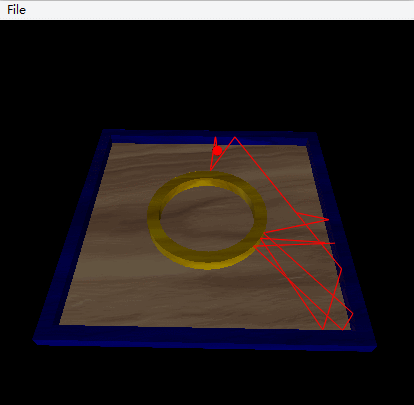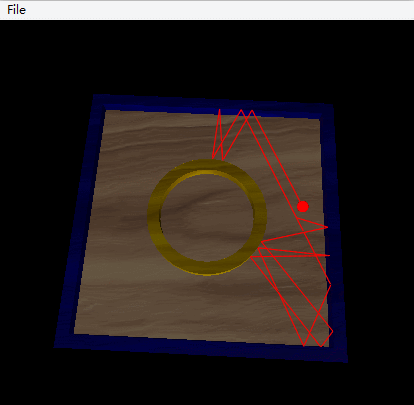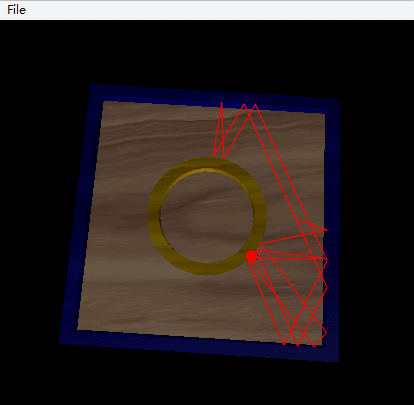
Another possibility is given by Vpython, this possibility is a square table with a circular interior wall located in the center.
Click the Code
-
Conclusion: In this situation, the trajectory is more complicated, the system is chaotic.
4. Reference and Acknowledgement
[1] Computational Physics (Second Edition), NIcholas J. Giordano, HIsao Nakanishi.
[1] Thanks to Chen Feng.