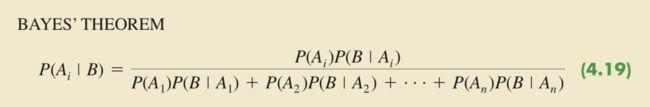概率是对一个被研究对象是否发生的可能性的一个数字度量。
在概率研究中,通过一系列活动取得随机变量的结果的过程称为试验 Experiment,试验的每一个可能结果称为样本点 Sample point,试验的所有可能的结果的集合称为样本空间 Sample space。这里需要注意的是每一次试验观察的对象可以是一个随机变量,也可以是多个随机变量,即一个样本点中可以包含多个不同的随机变量。在此基础上,还可以将具有某些共同特性的多个样本点归集到一起形成一个集合,称为一个事件 event。
计数法则 Counting rule,组合 Combination,排列 Permutations
为了确定样本空间中所包含的元素个数,需要用到上述标题中所提到的三个方面的知识。
计数法则
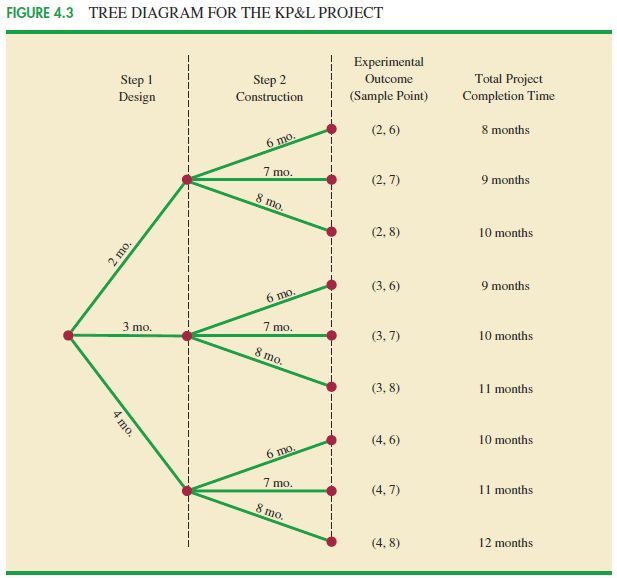
如果一个实验可以分 k 个步骤进行,每一步有 ni 个可能性,那么这个实验结果的总数为 n1n2...nk,对于这种分步试验,在统计可能的结果的时可以采用分步列表和树状图来辅助完成。
组合和排列
当我们从一个数据集 n 中一次性抽取 k 个样本(k ≤ n),并将这个小的样本组的内容作为实验的结果,或称一个事件时,就涉及到组合和排列问题:
当 k 个样本组的结果对顺序没有要求的时候,称为组合问题,此时这个抽样结果的取值的计算公式为:
- Cnk = n! / [k!(n - k)!]
当结果对于这 k 个抽样的顺序有要求的时候,称为排列问题,这个抽样结果的取值计算公式为:
- Pnk = n! / (n - k)!
排列与组合的结果的差异就在于这个 k 个元素之间的 k! 个顺序是否需要考量。
概率分配 Assigning Probabilities
在确定了抽样结果的所有可能取值以后,就需要考察各个取值结果的概率分配。
所谓的古典概型就是指样本空间中各个结果的概率是相等的,也就是说如果有 n 个可能的结果,那么取得每一个结果的概率为 1 / n
相对频数法:在大量重复试验后统计出各个结果出现的频数,每一个结果在全部实验中出现的频率就近似等于取得相应结果的概率
事件的概率:由于事件包含了多个样本点,如上图中所有项目周期为 9 个月的样本点的集合为一个事件,因此事件的概率等于其中所包含的全部样本点的概率的总和。
集合的交集 Intersection,并集 Union,补集 Complement
补集:由事件的定义可知其本质是一个集合,如果将事件记做 A,那么其余所有不在 A 中的样本点则构成另一个集合,称为 A 的补集,记做 Ac,且有 P(A) + P(Ac) = 1
交集:既在集合 A 中又在集合 B 中的样本点的集合,记做 A ∩ B
并集:包含所有事件 A 和 事件 B 中的样本点的集合,记作 A ∪ B, 由于集合中的元素是唯一的,因此在构造并集的时候,需要对 A 和 B 交集中的元素进行一次去重,因此 P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
互斥事件 Mutually exclusive
对于两个随机事件 A 和 B 来说,如果 A 发生的同时 B 不能发生,或者当 B 发生的同时 A 也不能发生,那么也就意味着 A ∩ B = 0,即二者没有共同的样本点,此时称 A 和 B为互斥事件。
条件概率 Conditional Probability
在很多情况下,由于不同的事件的定义是对被研究对象的不同角度的一个观测,因此定义在同一个样本集上的事件之间很可能彼此是有交叉的,即由于包含相同的样本点,一个事件的发生会对另外一个事件是否发生产生影响。此时,如果我们已知一个事件 A 发生的概率,但我们又获知事件 B 已经发生了,那么我们很可能可以利用这个新的信息进一步更新事件 A 发生的概率,更精确的描述 A 发生的概率,这个新的概率称为条件概率,记做 P(A | B),其计算公式为:
- P(A | B) = P(A ∩ B) / P(B)
直观的理解条件概率的公式就是如果在事件 B 已经发生的前提下,如果也想要观测到事件 A 发生,那么唯一可能就是造成事件 B 发生的样本点落在 A ∩ B 这一部分,那么这个交集部分在事件 B 中所占的比例就是在事件 B 已经发生的前提下事件 A 发生的概率。
在计算条件概率的时候,最重要的工作就是合理的定义事件,在此基础上可以将事件及其概率用表格清晰的展示出来,如下表所示:
这种可以记录多个事件及其相应概率的表格称为联合概率分布表,表格的交叉项记录的是两个事件交集的概率,被称为联合概率 joint probability,表格的边缘为单独一个事件的概率,由于被放在边缘位置,因此称为边缘概率 marginal probability。
在条件概率的基础上则有:
P(A ∩ B) = P(B)P(A | B) = P(A)P(B | A)
相互独立
如果 P(A | B) = P(A) 或者 P(B | A) = P(B),也即事件 A 或 事件 B 发生的概率对彼此没有影响,则称事件 A 和事件 B 相互独立,此时:
P(A ∩ B) = P(B)P(A | B) = P(A)P(B | A) = P(A)P(B)
需要注意的是,相互独立并不意味着没有交集,只是二者对于彼此发生的概率没有影响。并且如果两个事件互斥,则意味着一个事件发生的前提下,另一个事件发生的概率为 0,因此二者不是相互独立的。
贝叶斯原理 Bayes theorem
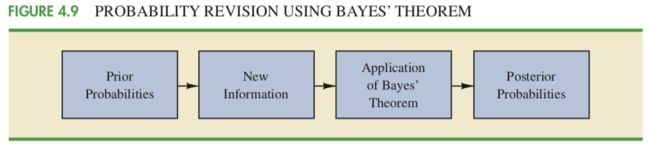
在实际应用中,我们一般会先通过分析历史数据或主观经验推断大致的得到事件 A 发生的概率 P(A),这个概率在条件概率的语境中被称为先验概率 Prior probability,而后随着研究的深入,可能会进一步获知其他相关事件 B 已经发生,此时,我们就可以根据条件概率更新事件 A 同时也发生的概率,即 P(A | B),这个新的概率值被称为后验概率 Posterior probability。
例如,假设一家工厂的某个零件来源于两个供应商 A1 和 A2,且 P(A1) = 0.65,P(A2) = 0.35。既往的质量检测发现两个供应商的良品 G 和不良品 B 的概率分别为:
P(G | A1) = 0.98,P(B | A1) = 0.02
P(G | A2) = 0.95,P(B | A2) = 0.05
此时如果后续生产由于不良品而导致停机时,这个不良品来自于 A1 和 A2 的概率分别是多少?
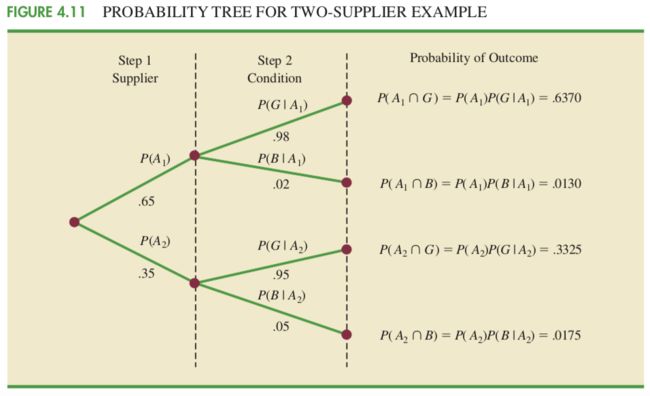
为了便于分析这个问题,我们可以采用绘制分步树状图的方式:
- 第一步根据所涉及的事件,分析事件定义,并绘制事件的分步树状图
第二步列出事件 A1 和 A2 的先验概率 P(A1),P(A2)
第三步列出在 A1 和 A2 已发生基础上的条件概率,并进一步计算相关事件的联合概率:
第四步计算出新增信息,在本例中指不良品率的概率:
- P(B) = P(A1 ∩ B) + P(A2 ∩ B) = P(A1)P(B | A1) + P(A2)P(B | A2)
第五步计算在不良品已经被检出的情况下,其来自 A1 和 A2 的概率,即:
P(A1 | B) = P(A1 ∩ B) / P(B) = P(A1)P(B | A1) / [P(A1)P(B | A1) + P(A2)P(B | A2)]
P(A2 | B) = P(A2 ∩ B) / P(B) = P(A2)P(B | A2) / [P(A1)P(B | A1) + P(A2)P(B | A2)]
条件概率最早由贝叶斯提出,因此相关理论也被称为贝叶斯原理,其在需要计算后验概率的事件彼此互斥且并集是样本空间的总体的情况下都适用。上述条件可以简记做 MECE,即 Mutually exclusive, collectively exhaustive。上例中供应商只有 A1 和 A2 两家,彼此互斥且二者的并集就是供应商样本空间的总体。
当存在 n 个满足这两个条件的事件 A1,A2 ... An时,当先验概率 P(A1),P(A2) ... P(An) 和对应的条件概率 P(B | A1),P(B | A2) ... P(B | An) 已知,则可以在求的联合概率后计算 P(B),上述事件 A1,A2 ... An 的后验概率可以进一步在 P(B) 的基础上依据贝叶斯原理更新为后验概率:
除了树状图外还可以使用列表的方式做相应的计算:
免责声明
我写这个笔记是为了系统的复习概率论中的一些概念,阅读的是 Statistics for Business and Economics, 12th Edition 英文原版,这是一本非常经典的参考书,毫无保留的满分推荐。尽管书名暗示了是在商业和经济学中的统计学,但根本的统计学知识是不变量,并且和很多优秀的原版书一样,作者时刻注意用实例来讲解统计学概念,基本上每一个新的概念的定义都建立在日常生活的实例的基础上,在此基础上还保留了精美的排版和精心设计的插图,十分便于理解。
笔记最重要的一个目的就是记录者复习的重要资料,如果能对别人也有所帮助那就是额外的奖赏了,所以为了复习方便我擅自截取了书中的很多插图,这些插图仅限于个人学习使用。其他人请勿直接转载,如转载请删除插图并附带这则免责声明,否则由此而产生的版权问题,请转载者自行承担。