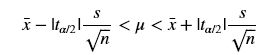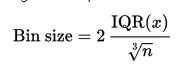谢谢余博的指导，Daisy同学的作业也有所启发。
第5课 中心极限定理 & 区间估计
本课基本作业
用t分布求房屋平均面积在95%的置信区间，数据为house_size.csv
t分布求置信区间公式
本课进阶作业
output_9_0.png
分布用t分布和bootstrap方法求年均降雨量在95%的置信区间，数据为rainfall.csv，该数据是英国谢菲尔德气象台记录的从1983年到2015年间的降雨量。
课堂回顾
导入模块和配置图像属性
import scipy.stats
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%config InlineBackend.figure_format = 'retina'
标准正态分布
standard_norm = scipy.stats.norm
x = np.arange(-4, 4, 0.01)
plt.plot(x, standard_norm.pdf(x))
plt.show()
标准正态分布示例图
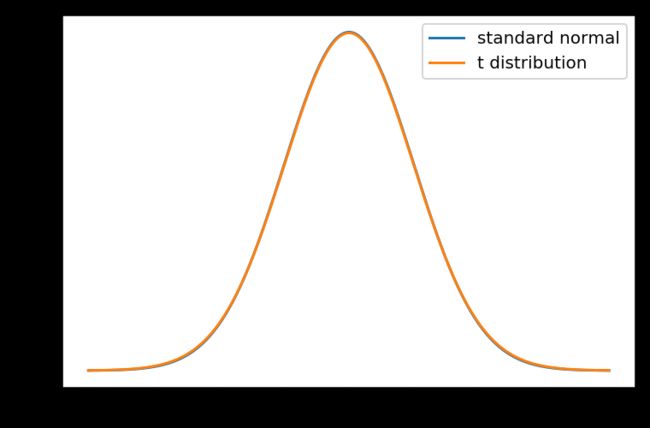
t分布
t_dist = scipy.stats.t
plt.plot(x, standard_norm.pdf(x), label='standard normal')
x = np.arange(-4, 4, 0.01)
plt.plot(x, t_dist.pdf(x, df=1), label='t distribution')
plt.legend()
plt.show()
自由度为1的t分布和标准正态分布对比
t_dist = scipy.stats.t
plt.plot(x, standard_norm.pdf(x), label='standard normal')
x = np.arange(-4, 4, 0.01)
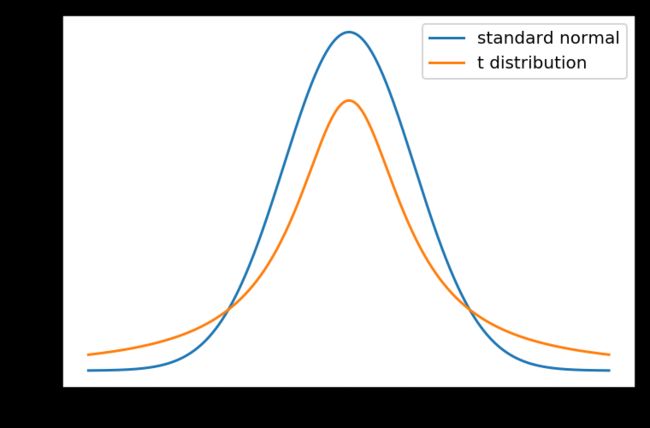
plt.plot(x, t_dist.pdf(x, df=99), label='t distribution')
plt.legend()
plt.show()
自由度为99的t分布和标准正态分布对比
当自由度df大于等于30时，t分布和标准整体分布可看作是一样的。上图是自由度为99时的t分布和标准正态分布的对比
置信区间
导入住房面积数据
house = pd.read_csv('G:\Dropbox\data-analysis\lesson5\house_size.csv', header=None)
house_size = house.iloc[:,0]
print(list(house_size))
[314, 119, 217, 326, 342, 318, 130, 465, 383, 396, 507, 283, 250, 326, 279, 363, 229, 303, 367, 246, 247, 262, 209, 294, 112, 249, 354, 355, 272, 277, 377, 411, 223, 232, 445, 333, 336, 349, 611, 516, 233, 275, 395, 241, 127, 228, 305, 321, 235, 226, 288, 503, 305, 280, 318, 281, 227, 279, 171, 290, 336, 284, 380, 314, 316, 476, 309, 293, 160, 300, 319, 396, 275, 212, 344, 305, 280, 331, 359, 283, 136, 322, 359, 202, 188, 187, 457, 340, 262, 288, 318, 381, 289, 205, 373, 200, 320, 213, 261, 357]
基本作业代码及结果
定义计算t分布置信区间的函数
def ci_t(data, confidence):
sample_mean = np.mean(data)
sample_std = np.std(data)
sample_size = len(data)
df = len(data) - 1
alpha = (1 - confidence) / 2
t_score = scipy.stats.t.isf(alpha, df)
ME = t_score * sample_std / np.sqrt(sample_size)
lower_limit = sample_mean - ME
upper_limit = sample_mean + ME
return (lower_limit, upper_limit)
t分布函数房屋平均面积数据在95%的置信区间返回结果
ci_t(house_size, 0.95)
(283.28723911352608, 318.41276088647396)
进阶作业代码及结果
导入年平均降雨量数据
house = pd.read_csv('G:\Dropbox\data-analysis\lesson5\house_size.csv', header=None)
rainfall = pd.read_csv('G:\Dropbox\data-analysis\lesson5\\rainfall.csv', header=None)
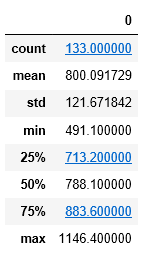
rainfall.describe()
rainfall describe()返回结果
rainfall_volume = rainfall.iloc[:,0]
用之前定义的t分布函数年平均降雨量数据在95%的置信区间
返回结果如下
ci_t(rainfall_volume, 0.95)
(779.30082422089879, 820.88263442571781)
用bootstrap方法求年平均降雨量数据在95%的置信区间
sample_size = len(rainfall_volume)
sample_size
133
def bootstrap_mean(data):
# 从数据data中重复抽样，样本大小与data相同，并返回样本均值
return np.mean(np.random.choice(data, size=len(data)))
def draw_bootstrap(data, times=1):
#初始化长度为times的空数组
bs_mean = np.empty(times)
#进行多次（times次）抽样，将每次得到的样本均值存储在bs_mean中
for i in range(times):
bs_mean[i] = bootstrap_mean(data)
return bs_mean
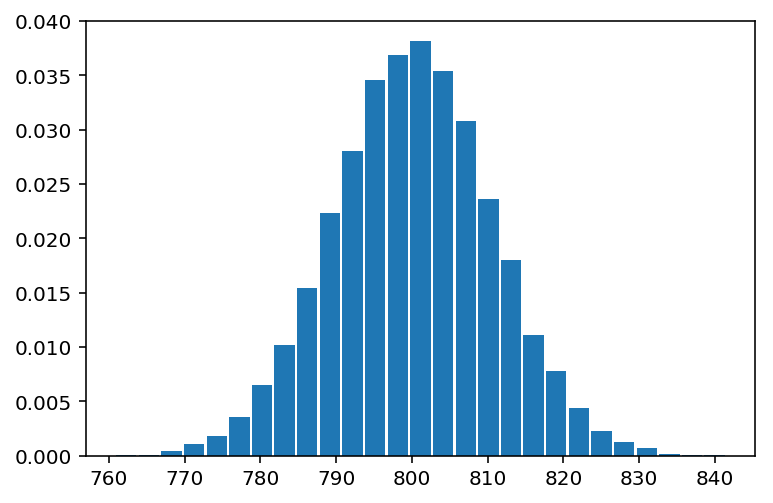
调用bootstrap函数生成10000个样本均值并显示图形。bins取27根据Freedman–Diaconis rule推导而的。
General equation for Freedman–Diaconis rule
bs_mean = draw_bootstrap(rainfall_volume, 10000)
plt.hist(bs_mean, bins=27, normed=True, rwidth=0.9)
plt.show()
10000个年平均降雨量数据的直方图
找出2.5%和97.5%百分位对应的样本均值，即为年平均降雨量数据在95%的置信区间。
np.percentile(bs_mean, [2.5, 97.5])
array([ 779.5668609 , 820.81815789])