因为不是科班出身,所以即使编程一段时间也时常感觉自身基础知识非常不扎实,于是在最近开始补习算法和计算机理论的基础知识。
目前看的算法书籍是《算法》(第四版),由Robert Sedgewick以及Kevin Wayne编写的,由于不可能把所有的练习都写成博客记录下来,于是就在学习过程中,挑选一些有意思的写成笔记,以便日后参考以及与同行互相交流。
今天要准备写的就是非常经典的牛顿迭代法求平方根,事实上现在的绝大部分编程语言中,标准库中都已经为我们准备好了计算平方根的函数,但是本着学习的精神,今天我们也要写出一个求平方根的函数。
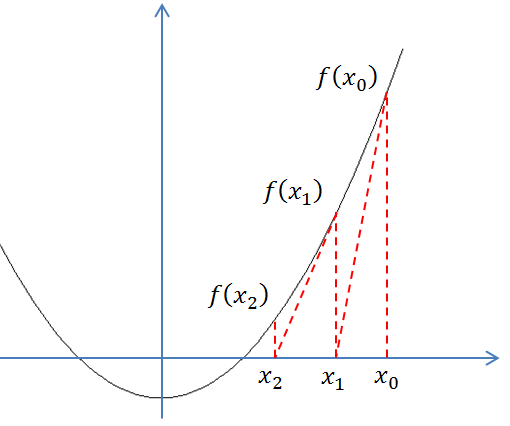
牛顿法是一种在实数域和复数域上近似求解方程的方法。方法使用函数 f(x)的泰勒级数的前面几项来寻找方程f(x)=0的根。首先我们先来看函数图像。
首先,选择一个接近函数f(x)零点的x0,计算相应的f(x0)和切线斜率f'(x0)(这里f'表示函数f的导数)。
也就是求如下方程的解:
我们将新求得的点 x坐标命名为x1,通常x1会比x0更接近方程f(x)=0的解。因此我们现在可以利用x1开始下一轮迭代。迭代公式可化简为如下所示:
而求平方根的方程我们可以看成f(x) = x^2 - a,a即为我们要求平方根的常数。
于是在算法代码的编写上,我们也可以用这种猜的思想,来近似求解这个平方根,我们需要定义一个精度,若Xn+1-Xn的值小于我们的精度值,那么我们即可以认为Xn为我们要求的解。
所以算法代码编写如下(采用Java示例)。
/**
* 牛顿迭代法求平方根
* @param number 求值的数
* @param accuracy 精度
* @return Double
*/
public static double NewtonSqrt(double number, double accuracy) {
//第一个猜测值
double guess = number / 2;
int count = 0;
if (number < 0) {
return Double.NaN;
}
//当两个猜测的差值大于精度即return
while (Math.abs(guess - (number / guess)) > accuracy) {
//迭代公式推导而成
guess = (guess + (number / guess)) / 2;
count++;
System.out.printf("try count = %d, guess = %f\n", count, guess);
}
System.out.printf("final result = %f\n", guess);
return guess;
}
牛顿迭代法求平方根的代码就如上面所示,而接下来为了体现牛顿迭代法的优势,我们再写一个二分法计算平方根的算法,来对比:
public static double DichotomySqrt(double number, double accuracy) {
double higher = number;
double lower = 0.0;
double middle = (lower + higher) / 2;
double last_middle = 0.00;
int count = 0;
if (number < 0) {
return Double.NaN;
}
while (Math.abs(middle - last_middle) > accuracy) {
if (middle * middle > number) {
higher = middle;
} else {
lower = middle;
}
last_middle = middle;
middle = (lower + higher) / 2;
count++;
System.out.printf("Dichotomy try count = %d, guess = %f\n", count, last_middle);
}
System.out.printf("Dichotomy final result = %f\n", last_middle);
return last_middle;
}
二分法的讲解就不多说了,跟牛顿迭代法的验证结果相似,看精度差是否在定义范围内。
那么接下来我们来测试二分法和牛顿迭代法求值的效率。
public static void main(String[] args) {
double result = NewtonSqrt(2,1e-3);
double dichotomyRes = DichotomySqrt(2,1e-3);
}
先看小精度情况下,求2的平方根
try count = 1 guess = 1.5
try count = 2 guess = 1.4166666666666665
try count = 3 guess = 1.4142156862745097
final result = 1.4142156862745097
Dichotomy try count = 1 guess = 1.0
Dichotomy try count = 2 guess = 1.5
Dichotomy try count = 3 guess = 1.25
Dichotomy try count = 4 guess = 1.375
Dichotomy try count = 5 guess = 1.4375
Dichotomy try count = 6 guess = 1.40625
Dichotomy try count = 7 guess = 1.421875
Dichotomy try count = 8 guess = 1.4140625
Dichotomy try count = 9 guess = 1.41796875
Dichotomy try count = 10 guess = 1.416015625
Dichotomy final result = 1.416015625
可以看到牛顿迭代法计算了3次,二分法计算了10次。
而精度稍大的时候
public static void main(String[] args) {
double result = NewtonSqrt(2,1e-15);
double dichotomyRes = DichotomySqrt(2,1e-15);
}
try count = 1 guess = 1.5
try count = 2 guess = 1.4166666666666665
try count = 3 guess = 1.4142156862745097
try count = 4 guess = 1.4142135623746899
try count = 5 guess = 1.414213562373095
final result = 1.414213562373095
Dichotomy try count = 1 guess = 1.0
Dichotomy try count = 2 guess = 1.5
Dichotomy try count = 3 guess = 1.25
Dichotomy try count = 4 guess = 1.375
Dichotomy try count = 5 guess = 1.4375
Dichotomy try count = 6 guess = 1.40625
Dichotomy try count = 7 guess = 1.421875
Dichotomy try count = 8 guess = 1.4140625
Dichotomy try count = 9 guess = 1.41796875
Dichotomy try count = 10 guess = 1.416015625
Dichotomy try count = 11 guess = 1.4150390625
Dichotomy try count = 12 guess = 1.41455078125
Dichotomy try count = 13 guess = 1.414306640625
Dichotomy try count = 14 guess = 1.4141845703125
Dichotomy try count = 15 guess = 1.41424560546875
Dichotomy try count = 16 guess = 1.414215087890625
Dichotomy try count = 17 guess = 1.4141998291015625
Dichotomy try count = 18 guess = 1.4142074584960938
Dichotomy try count = 19 guess = 1.4142112731933594
Dichotomy try count = 20 guess = 1.4142131805419922
Dichotomy try count = 21 guess = 1.4142141342163086
Dichotomy try count = 22 guess = 1.4142136573791504
Dichotomy try count = 23 guess = 1.4142134189605713
Dichotomy try count = 24 guess = 1.4142135381698608
Dichotomy try count = 25 guess = 1.4142135977745056
Dichotomy try count = 26 guess = 1.4142135679721832
Dichotomy try count = 27 guess = 1.414213553071022
Dichotomy try count = 28 guess = 1.4142135605216026
Dichotomy try count = 29 guess = 1.414213564246893
Dichotomy try count = 30 guess = 1.4142135623842478
Dichotomy try count = 31 guess = 1.4142135614529252
Dichotomy try count = 32 guess = 1.4142135619185865
Dichotomy try count = 33 guess = 1.4142135621514171
Dichotomy try count = 34 guess = 1.4142135622678325
Dichotomy try count = 35 guess = 1.4142135623260401
Dichotomy try count = 36 guess = 1.414213562355144
Dichotomy try count = 37 guess = 1.4142135623696959
Dichotomy try count = 38 guess = 1.4142135623769718
Dichotomy try count = 39 guess = 1.4142135623733338
Dichotomy try count = 40 guess = 1.4142135623715149
Dichotomy try count = 41 guess = 1.4142135623724243
Dichotomy try count = 42 guess = 1.414213562372879
Dichotomy try count = 43 guess = 1.4142135623731065
Dichotomy try count = 44 guess = 1.4142135623729928
Dichotomy try count = 45 guess = 1.4142135623730496
Dichotomy try count = 46 guess = 1.414213562373078
Dichotomy try count = 47 guess = 1.4142135623730923
Dichotomy try count = 48 guess = 1.4142135623730994
Dichotomy try count = 49 guess = 1.4142135623730958
Dichotomy try count = 50 guess = 1.414213562373094
Dichotomy final result = 1.414213562373094
这里就一目了然了,所以有时候,写代码一定不能想着功能实现了就好,在算法的效率上一定要多多思考。
不再举栗子了,免得有凑字数的嫌疑。下次再讨论咯。