3. 1 抽象数据类型
抽象数据类型(abstractdata type, ADT)是带有一组操作的一些对象的集合。抽象数据类型是数学的抽象;在ADT的定义中没有地方提到关于这组操作是如何实现的任何解释。 诸如表、集合、图以及与它们各自的操作一起形成的这些对象都可以被看做是抽象数据类型。
Java类也考虑到ADT的实现,不过适当地隐藏了实现的细节。 这样,程序中需要对ADT实施操作的任何其他部分可以通过调用适当的方法来进行。 如果由于某种原因需要改变实现的细节,那么通过仅仅改变执行这些ADT操作的例程应该是很容易做到的。 这种改变对于程序的其余部分是完全透明的。
对于每种ADT并不存在什么法则来告诉我们必须要有哪些操作,这是一个设计决策。 错误处理和结构调整(在适当的地方)一般也取决于程序的设计者。 本章中将要讨论的这三种数据 [ill 结构是ADT的 最基本的例子。我们将会看到它们中的每一种是如何以多种方法实现的,不过,当它们被正确地实现以后,使用它们的程序却没有必要知道它们是如何实现的。
3.2 表ADT
我们将处理形如A0 , A1, A2 …, AN-1的一般的表。 我们说这个表的大小是N。 我们将大小为0 的特殊的表称为空表(emptylist)。
对于除空表外的任何表,我们说 Ai后继 Ai-1 (或继 Ai-1之后,i < N)并称 Ai-1前驱 Ai (i >0)。表中的第一个元素是 A0,而 最后一个元素是 AN-1。 我们将不定义 A0的前驱元,也不定义 AN-1的后继元。 元素Ai 在表中的位置为i + 1。 为了简单起见,我们假设表中的元素是整数,但一般说来任意的复元素也是允许的(而且容易由Java泛型类处理)。
与这些“定义”相关的是要在表ADT上进行操作的集合。prinTList和makeEmpty是常用的操作,其功能显而易见;find返回某一项首次出现的位置;insert和remove一般是从表的某个位置插入和删除某个元素;而findKth则返回(作为参数而被指定的)某个位置上的元素。如果34,12, 52, 16, 12是一个表,则find(52)会返回2;insert(x, 2)可把表变成34,12, x, 52, 16, 12(如果我们插入到给定位置上的话);而remove(52)则又将该表变为 34, 12 , X, 16 , 12。
3. 2. 1 表的简单数组实现
对表的所有这些操作都可以通过使用数组来实现。虽然数组是由固定容量创建的,但在需要的时候可以用双倍的容量创建一个不同的数组。它解决由于使用数组而产生的最严重的问题,即从历史上看为了使用一个数组,需要对表的大小进行估计。而这种估计在Java或任何现代编程语言中都是不需要的。下列程序段解释一个数组arr 在必要的时候如何被扩展(其初始长度为10):
数组的实现可以使得printList 以线性时间被执行,而findKth 操作则花费常数时间,这正是我们所能够预期的。不过,插入和删除的花费却潜藏着昂贵的开销,这要看插入和删除发生在什么地方。最坏的情形下,在位置0的插入(即在表的前端插入)首先需要将整个数组后移一个位置以空出空间来,而删除第一个元素则需要将表中的所有元素前移一个位置,因此这两种操作的最坏情况为O(N)。平均来看,这两种操作都需要移动表的一半的元素,因此仍然需要线性时间。另一方面,如果所有的操作都发生在表的高端,那就没有元素需要移动,而添加和删除则只花费0(1 )时间。
存在许多情形,在这些情形下的表是通过在高端进行插入操作建成的,其后只发生对数组的访问(即只有findKth 操作)。在这种情况下,数组是表的一种恰当的实现。然而,如果发生对表的一些插入和删除操作,特别是对表的前端进行,那么数组就不是一种好的选择。
3.2.2 简单链表
为了避免插入和删除的线性开销,我们需要保证表可以不连续存储,否则表的每个部分都可能需要整体移动。图3-1 指出链表的一般想法。
链表由一系列节点组成,这些节点不必在内存中相连。每一个节点均含有表元素和到包含该元素后继元的节点的链(link)。我们称之为next 链。最后一个单元的next链引用null 。
为了执行prinList或find(x), 只要从表的第一个节点开始然后用一些后继的next链遍历该表即可。这种操作显然是线性时间的,和在数组实现时一样,不过其中的常数可能会比用数组实现时要大。findKth 操作不如数组实现时的效率高; findKth(i) 花费0(i) 的时间并以这种明显的方式遍历链表而完成。在实践中这个界是保守的,因为调用findKth 常常是以(按i ) 排序后的方式进行。例如, findKth(2), findKth (3), findKth( 4) 以及findKth(6)可通过对表的一次扫描同时实现。
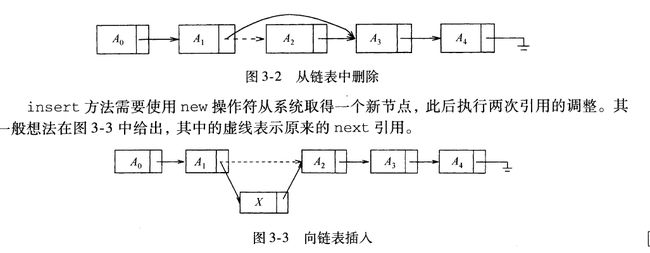
remove 方法可以通过修改一个next 引用来实现。图3-2 给出在原表中删除第三个元素的结果。
我们看到,在实践中如果知道变动将要发生的地方,那么向链表插入或从链表中删除一项的操作不需要移动很多 的项,而只涉及常数个节点链的改变。在表的前端添加项或删除第一项的特殊情形此时也属于常数时间的操作,当然要假设到链表前端的链是存在的。只要我们拥有到链表最后节点的链,那么在链表末尾进行添加操作的特殊情形(即让新的项成为最后一项)可以花费常数时间。因此,典型的链表拥有到该表两端的链。删除最后一项比较复杂,因为必须找出指向最后节点的项,把它的next链改成null , 然后再更新持有最后节点的链。在经典的链表中,每个节点均存储到其下一节点的链,而拥有指向最后节点的链并不提供最后节点的前驱节点的任何信息。
保留指向最后节点的节点的第3个链的想法行不通,因为它在删除操作期间也需要更新。我们的做法是,让每一个节点持有一个指向它在表中的前驱节点的链,如图3-4所示,我们称之为双链表(doubly linked list)。
3. 3 Java Collections API中的表
在类库中,Java语言包含有一些普通数据结构的实现。该语言的这一部分通常叫作Collections API。表ADT是在Collections API中实现的数据结构之一。我们将在第4章看到其他一些数据结构。
3. 3. 1 Collecction接口
Collections API位于java.util包中。集合(collection)的概念在Collection接口中得到抽象,它存储一组类型相同的对象。图3-5显示该接口一些最重要的部分(但一些方法未被显示)。
在Collection接口中的许多方法所做的工作由它们的英文名称可以看出.Collection接口扩展了Iterable接口。实现Iterable接口的那些类可以拥有增强 的for循环,该循环施于这些类之上以观察它们所有的项。例如,图3-6中的例程可以用来打印任意集合中的所有的项。这种方式的print的实现和当coll具有类型AnyType[]时能够使用的相应的实现是完全相同的,它们逐个字符都是一样的。
3.3.2 Iterator接口
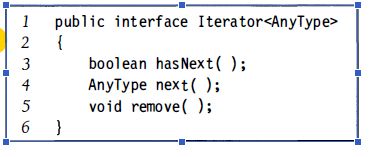
实现Iterable 接口的集合必须提供一个称为iterator 的方法,该方法返回一个Iterator类型的对象。该Iterator 是一个在java.util 包中定义的接口,见图3-7。
Iterator 接口的思路是,通过Iterator 方法,每个集合均可创建并返回给客户一个实现Iterator 接口的对象,并将当前位置的概念在对象内部存储下来。
每次对next 的调用都给出集合的(尚未见到的)下一项。因此,第1 次调用next 给出第1 项,第2 次调用给出第2 项,等等。hasNe 立用来告诉图3-7 java. u口1 包中的巨erator 接口是否存在下一项。当编译器见到一个正在用于Iterator 的对象的增强的for 循环的时候,它用对iterator 方法的那些调用代替增强的for 循环以得到一个Iterator 对象,然后调用next和hasNext。因此,前面看到的print例程由编译器重写,见图3-8 所示。
由于Iterator 接口中的现有方法有限,因此,很难使用Iterator做简单遍历Collection以外的任何工作。Iterator接口还包含一个方法,叫作remove 。该方法可以删除由next最新返回的项(此后,我们不能再调用remove, 直到对next再一次调用以后)。虽然Collection接口也包含一个remove方法,但是,使用巨erator 的remove方法可能有更多的优点。
Iterator的remove方法的主要优点在于,Collection 的remove方法必须首先找出要被删除的项。如果知道所要删除的项的准确位置,那么删除它的开销很可能要小得多。下一节我们将要看到一个例子,是在集合中每隔一项删除一项。这个程序用迭代器(iterator)很容易编写,而且比用Collection的remove方法潜藏着更高的效率。
当直接使用Iterator(而不是通过一个增强的for循环间接使用)时, 重要的是要记住一个基本法则:如果对正在被迭代的集合进行结构上的改变(即对该集合使用add、remove或clear方法), 那么迭代器就不再合法(并且在其后使用该迭代器时将会有Concurrent-ModificationException异常被抛出)。为避免迭代器准备给出某一项作为下一项( nextitem)而该项此后被删除,或者也许一个新的项正好插入该项的前面这样一些讨厌的情形,有必要记住上述法则。这意味着,只有在需要立即使用一个迭代器的时候,我们才应该获取迭代器。然而,如果迭代器调用了它自己的remove方法,那么这个迭代器就仍然是合法的。这是有时候我们更愿意使用迭代器的remove方法的第二个原因。
3.3.3 List接口、ArrayList类和LinkedList类
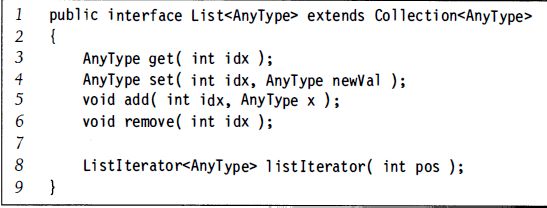
本节跟我们关系最大的集合就是表(list) , 它由java.util包中的List接口指定。List接口继承了Collection接口,因此它包含Collection接口的所有方法,外加其他一些方法。图3-9解释其中最重要的一些方法。
List ADT有两种流行的实现方式。ArrayList类提供了List ADT的—种可增长数组的实现。使用ArrayList的优点在于,对get和set的调用花费常数时间。其缺点是新项的插入和现有项的删除代价昂贵,除非变动是在ArrayList的末端进行。LinkedList类则提供了List ADT的双链表实现。使用LinkedList的优点在于,新项的插入和现有项的删除均开销很小, 这里假设变动项的位置是已知的。这意味着,在表的前端进行添加和删除都是常数时间的操作, 由此LinkedList更提供了方法addFirst 和removeFirst、addLast 和remove Last以及getFirst和getLast等以有效地添加、删除和访问表两端的项。使用LinkedList的缺点是它不容易作索引,因此对get的调用是昂贵的,除非调用非常接近表的端点(如果对get的调用是对接近表后部的项进行,那么 搜索的进行可以从表的后部开始)。
这里,ArrayList的运行时间是O(N),但对于LinkedList来说,其运行时间则是O(N2),因为在LinkedList中,对get的调用为 O(N)操作。 可是,要是使用一个增强的for循环,那么它对任意List的运行时间都是O(N),因为迭代器将有效地从项到下一项推进。
对搜索而言,ArrayList和LinkedList都是低效的,对Collection的contains和remove两个方法(它们都以 AnyType 为参数)的调用均花费线性时间。
在ArrayList中有一个容量的概念,它表示基础数组的大小。 在需要的时候,ArrayList将自动增加其 容最以保证它至少具有表的大小。 如果该大小的早期估计存在,那么 ensureCapacity可以设置 容量为一个足够大的最以避免数组 容量以后的扩展。再有,trimToSize可以在所有的ArrayList添加操作完成之后使用以避免浪费空间。
3.4ArrayList类的实现
https://gitee.com/sunyunjie/DataStrycturesAndAlgorithmAnalysis
3.5LinkedList类的实现
https://gitee.com/sunyunjie/DataStrycturesAndAlgorithmAnalysis
3.6 栈ADT
3. 6. 1 栈模型
3. 6. 1 栈模型
栈(stack)是限制插入和删除只能在一个位置上进行的表,该位置是表的末端,叫作栈的顶(top)。对栈的基本操作有push(进栈)和pop(出栈),前者相当于插入,后者则是删除最后插入的元素。最后插入的元素可以通过使用top例程在执行pop之前进行考查。对空栈进行的pop或top一般被认为是栈ADT中的一个错误。另一方面,当运行push时空间用尽是一个实现限制,但不是ADT错误。
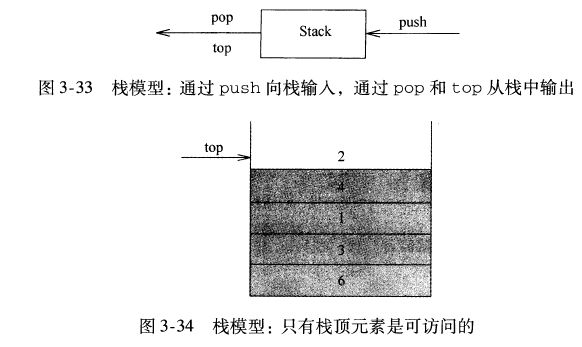
栈有时又叫作LIFO(后进先出)表。在图3-33中描述的模型只象征着push是输入操作而pop和top是输出操作。普通的清空栈的操作和判断是否空栈的测试都是栈的操作指令系统的一部分,但是,我们对栈所能够做的,基本上也就是push和pop操作。
图3-34表示在进行若干操作后的一个抽象的栈。一般的模型是,存在某个元素位于栈顶,而该元素是唯一的可见元素。
3.6.2 栈的实现
由于栈是个表,因此任何实现表的方法都能实现栈。显然,ArrayList和LinkedList都支持栈操作;99%的时间它们都是最合理的选择。偶尔设计一种特殊目的的实现可能会更快(例如,如果被放到栈上的项属于基本类型)。因为栈操作是常数时间操作,所以,除非在非常独特的环境下,这是不可能产生任何明显的改进的。对于这些特殊的时机,我们将给出两个流飞盯行的实现方法,一种方法使用链式结构,而另一种方法则使用数组,二者均简化了在ArrayList和LinkedList中的逻辑,因此我们不提供代码。
栈的链表实现
栈的第一种实现方法是使用单链表。通过在表的顶端插入来实现push,通过删除表顶端元素实现pop。top操作只是考查表顶端元素并返回它的值。有时pop操作和top操作合二为一。
栈的数组实现
另一种实现方法避免了链而且可能是更流行的解决方案。由于模仿ArrayList的add 操作,因此相应的实现方法非常简单。与每个栈相关联的操作是让theArray和topOfStack, 对于空栈它是- 1 (这就是空栈初始化的做法)。为将某个元素x推入栈中,我们使topOfStack增1然后置theArray [topOfStack] = x。为了弹出栈元素,我们置返回值为theArray[topOfStack]然后使topOfStack减1。
注意,这些操作不仅以常数时间运行,而且是以非常快的常数时间运行。在某些机器上,若在带有自增和自减寻址功能的寄存器上操作,则(整数的)push和pop都可以写成一条机器指令。最现代化的计算机将栈操作作为它的指令系统的一部分,这个事实强化了这样一种观念,即栈很可能是在计算机科学中在数组之后的最基本的数据结构。
3. 7 队列 ADT
像栈一样,队列(queue)也是表。然而,使用队列时插入在一端进行而删除则在另一端进行。
3. 7. 1 队列摸型
队列的基本操作是enqueue(入队),但是在表的末端( 叫作队尾(rear))插入一个元素,和dequeue(出队),它是删除(并返回)在表的开头(叫作队头(front))的元素。图3-37显示一个队列的图3-37 队列模型抽象模型。
3. 7.2 队列的数组实现
如同栈的情形一样,对于队列而言任何的表的实现都是合法的。像栈一样,对于每一种操作,链表实现和数组实现都给出快速的O(1)运行时间。队列的链表实现是简单直接的,我们留作练习。下面讨论队列的数组实现。
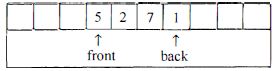
对于每一个队列数据结构,我们保留一个数组theArray以及位置front和back,它们代表队列的两端。我们还要记录实际存在于队列中的元素的个数currentSize。下图表示处于某个中间状态的一个队列。
操作应该是清楚的。为使一个元素x 入队(即执行enqueue) , 我们让currentSize 和back增1,然后置七heArray[back] = x。若使元素dequeue (出队), 我们置返回值为theArray[front],且currentSize减1然后使front增1。也可以有其他的方法(将在后面讨论)。现在论述错误检测。
上述实现存在一个潜在的问题。经过10次enqueue后队列似乎是满了,因为back现在是数组的最后一个下标,而下一次再enqueue就会是一个不存在的位置。然而,队列中也许只存在几个元素,因为若干元素可能已经出队了。像栈一样,即使在有许多操作的情况下队列也常常不是很大。
简单的解决方法是,只要front或back到达数组的尾端,它就又绕回到开头。下面诸图显示在某些操作期间的队列情况。这叫作循环数组(circular array)实现。
实现回绕所需要的附加代码是极小的(不过它可能使得运行时间加倍)。如果front或back增l导致超越了数组,那么其值就要重置到数组的第一个位置。
小结
本章描述了一些ADT的概念,并且利用三种最常见的抽象数据类型(ADT)阐述了这种概念。 主要目的就是将抽象数据类型的具体实现与它们的功能分开。 程序必须知道操作都做些什么,但是如果不知道如何去做那就更好。
表、栈和队列或许在全部计算机科学中是三个基本的数据结构,大量的例子证明了它们广泛的用途。 特别地,我们看到栈是如何用来记录过程和方法调用的,以及递归实际上是如何实 现的。 这对于我们的理解非常重要,其原因不只因为它使得过程语言成为可能,而且还因为知 道递归的实现从而消除了围绕其使用的大量谜团。 虽然递归非常强大,但是它并不是完全随意 的操作;递归的误用和乱用可能导致程序崩溃。