前言
本资料整理了高光谱遥感图像概念定义、分析处理与分类识别的基本知识。第一部分介绍高光谱图像的一般性原理和知识,第二部分介绍了高光谱图像的噪声问题;第三部分介绍高光谱图像数据冗余问题以及数据降维解决冗余的方法;第四部分介绍高光谱图像的混合像元问题,对光谱解混做了一定介绍;第五部分和第六部分分别介绍了高光谱图像的监督分类和分监督分类的特点、流程和常用算法。
1.基本介绍
高光谱遥感(Hyperspectral remote sensing) 是将成像技术和光谱技术相结合的多维信息获取技术,同时探测目标的二维集合空间与一维光谱信息,获取高光谱分辨率的连续、窄波段图像数据。
高光谱图像与高分辨率图像、多光谱图像不同。
高光谱识别优势:
光谱分辨率高、波段众多,能够获取地物几乎连续的光谱特征曲线,并可以根据需要选择或提取特定波段来突出目标特征;
同一空间分辨率下,光谱覆盖范围更宽,能够探测到地物更多对电磁波的响应特征;
波段多,为波段之间的相互校正提供了便利;
定量化的连续光谱曲线数据为地物光谱机理模型引入图像分类提供了条件;
包含丰富的辐射、空间和光谱信息,是多种信息的综合载体。
高光谱在识别方面的困难:
- 数据量大,图像包含几十个到上百个波段,数据量是单波段遥感图像的几百倍;数据存在大量冗余,处理不当,反而会影响分类精度;
- 对高光谱图像的分类一方面要求更高的光谱定标和反射率转换的精度,另一方面又因为成像机理复杂,数据量巨大而导致对图像数据预处理困难,包括大气矫正、几何校正、光谱定标和反射率转换等;
- 波段多、波段间的相关性高,因此分类需要的训练样本数目大大增多,往往因训练样本不足导致得到的训练参数不可靠(维数灾难);
- 针对常规遥感的处理模型和方法不能满足高光谱图像分类的需要。主要问题之一是统计学分类模型的参数估计问题,其对光谱特征的选择要求很高。
高光谱图像分类中的Hughes 现象:
Hughes现象:在机器学习问题中,需要在高维特征空间(每个特征都能够取一系列可能值)的有限数据样本中学习一种“自然状态”(可能是无穷分布),要求有相当数量的训练数据含有一些样本组合。给定固定数量的训练样本,其预测能力随着维度的增加而减小。
在高光谱遥感图像中,当训练样本数目有限时,分类精度随着图像波段数目的增加先增加,在到达一定极值后,分类精度随这波段数目的增加而下降。
传统遥感图像分析是利用图像空间信息,高光谱图像分析的核心是光谱分析。高光谱的遥感数据是一个光谱图像立方体,其最主要的特点将图像空间维与光谱维信息合为一体,与单波段相比,多出了一维光谱信息。在获取地表空间图像同时,会得到每个像元对应的地物光谱信息。
上图分别是某波段的遥感影像图和某像元的光谱特征图。
2.高光谱数据噪声处理
高光谱图像精细光谱数据能够充分反映地物光谱的细微特征。依据不同地物在光谱特征上的相对差异就可实现地物类别区分,实现目标探测和精细分类。
但是,由于成像光谱仪波段通道很密而造成光成像能量不足,故相对全色图而言,高光谱图像的信噪比(SNR)提高比较困难。在图像数据的获取过程中,地物光谱特征在噪声的影响下容易产生“失真”。另外由于高光谱数据量大,在精细分类过程中,往往需要对数据进行降维处理,而在降维过程中需要最大限度保留信号和压缩噪声,所以精确的噪声评估很有必要。另外噪声对精细分类的结果也有最直接影响。所以需要对高光谱数据进行噪声评估。
主要的噪声认为是高斯白噪声,分为加性噪声和乘性噪声。
噪声评估主要有三种方法:实验室法、暗电流法和图像法。由于前两种方法在实验中难以实现,广泛应用的是第三种——图像法。
图像法分为以下几种:
-
均匀区域法(HA)
主要思想:从图像中选取四个以上均匀区域,通过计算这些均匀区域标准差的平均值获取图像噪声的估计值。
不足:需要人工进行均匀区域选择,无法自动化;满足条件的均匀区域在大部分遥感图中并不存在;子区域噪声估计并不能代表整幅图像的噪声。
-
地学统计法(GS)
主要思想:从图像中选择几条均匀的窄条带,通过对这些窄条带的半方差函数的计算实现对图像噪声的估算。一定程度上利用了成像光谱数据的空间相关性。
不足:与均匀区域法相似。
-
局部均值与局部标准差法(LMLSD)
主要思想:假定图像由大量均匀的小块构成,且噪声以加性噪声为主。使用局部均值和局部标准差的概念,将图像分割为很多小块,然后计算这些子块的标准差作为局部噪声大小,并选择包含子块数最多区间的局部标准差的平均值作为整个图像的最佳噪声估计。
不足:只对高斯白噪声有效,对高斯随机噪声的图像,信号被噪声干扰。
-
空间/光谱维去相关法(SSDC)
主要思想:是一种专门针对高光谱图像的噪声评估方法,利用高光谱图像空间维和光谱维存在高相关性的特点,通过多元线性回归去除具有高相关性的信号,利用得到的残差图像对噪声进行估算。
评价:该方法受地物覆盖类型影响小,并且可以自动执行,是目前较为稳定的高光谱图像噪声评价方法。
3.高光谱图像数据降维的常用方法
高光谱遥感图像所具有的大量光谱波段为地物信息提取提供了极其丰富的信息,有利于更精细的地物分类,然而波段的增多也会导致信息的冗余和数据处理复杂性的提高。
数据降维满足下面条件:尽可能保留数据的特征信息;去除数据冗余与相关性。
主要从特征选择和特征提取两方面进行降维处理。
3.1 特征选择
特征选择是光谱组合,即从原光谱波段数为$N$的波段中选择$M$个波段$(N>M)$,可能的光谱组合数为
$$
\frac{N!}{M!(N-M)!}
$$
在这里可以采用Band Index 方法进行光谱波段选择降维。
Band Index 方法:Hyperspectral 遥感图像根据相关性分为$K$组(如shortwave light、visible light、near-infrared),设每个组中的波段数为 $n_l(l=1,2,\cdots , k)$。用$p {ij}$ 表示波段$i$ 与波段$j$的相关系数 ,$\sigma_i$ 表示波段$i$的方差,$R_a$表示波段$i$与不同组其他波段相关系数的绝对值的和,$R_w$ 表示波段$i$与同组其他波段的相关系数的绝对值的均值,则有
$$
R_w = \frac{1}{n_l} \sum |p{ij}|
$$
从而波段$i$的Band Index 可表示为:
$$
P_i = \frac {\sigma_i}{R_a+R_w}
$$
通过观察,我们知道随着方差增大,波段包含的信息越多;随着相关系数降低,波段的独立性越高。
Band Index 是一个重要参数,其反映了波段总体包含特征信息和相关性。
通过结合Band Index 和目标物体有效的光谱范围(effiective spectral scope of object),我们可以进行波段选择,进而下一步识别分类。
3.2 特征提取
高光谱的数据降维技术是以图像特征提取为目的,利用低维数据来有效地表达高维数据的特征,同时也压缩了数据量,更有利于信息的快速提取。数据降维包含的内容非常广泛,高光谱遥感图像主要以降低光谱维度和提取光谱维度特征为主。
上一节的特征选择就讲到了在原始特征空间进行特征选择形成原始空间的一个子空间的特征选择方法,接下来介绍线性变换方法 :$Y=BX$ ,从高维数据空间中,产生一个合适的低维子空间(不是简单的特征选择组合),使数据在这个空间的分布可以在某种最优意义上描述原来的数据。
3.2.1 主成分分析
主成分分析(PCA)是最基本的高光谱数据降维方法,在高光谱数据压缩、去相关、消噪和特征提取中发挥了巨大的作用。PCA 变换又称为霍特林变换(hotelling transform)和K-L (karhunen-loeve)变换。变换后的各主成分分量彼此不相关,且随主成分编号的增加该分量包含的信息量减少。
在高光谱遥感数据的PCA变换中,一般将每个波段当作一个向量来处理,设高光谱遥感数据有$p$个波段,图像空间维度为$m \times n$,则具体处理流程:
- 图像向量化:输入图像数据可以表示成$\bf{X = (x_1,x_2,\cdots, x_p)^T}$,其中 $x_i$ 表示为一个 $N \times 1$ 列向量,这里有$N=m \times n$。即将图像按行或按列展开有规则连接起来,称为一个向量。
- 向量中心化:将向量组中的所有向量减去向量组的均值向量,即 $\bf{Y =X-E(X)}$。
- 计算向量组 $\bf{Y}$ 的协方差矩阵 $\Sigma$。
- 求协方差矩阵 $\Sigma$的特征值矩阵 $\Lambda$ 和特征向量矩阵 $\bf{A}$。
- 进行主成分变换, $\bf{Z=A^TY}$。
PCA变换是基于信息量的一种正交线性变换,变换后的图像信息主要集中在前几个主成分分量中,在变换域中丢弃信息量小的成分分量,经过反变换后仍能得到复原图像的近似图像。
在PCA变换的基础上提出了分块主成分分析方法、定向主成分分析方法(DPCA)和选择主成分方法(selective PCA)。
但PCA 变换存在两个明显的缺陷:一是图像数值变换影响明显;二是变换后的信噪比并不一定随着主成分编号的增加而降低。针对这两个问题分别发展了标准化的PCA(standardized PCA, SPCA) 和残差调整的PCA(residual-scaled PCA, RPCA)。
3.2.2 最大噪声分数变换
当噪声方差或噪声在图像各波段分布不均匀时,基于方差最大化的PCA方法并不能保证图像质量随着主成分的增大而降低。所以这里引入最大噪声分数(maximum noise fraction,MNF) 变换 ,该变换根据图像质量排列成分。MNF 方法主要采用SNR和噪声比例来描述图像质量参数。
假设$\bf{X = [x_1,x_2,\cdots, x_p]^T}$是 $p \times N$ 矩阵,行向量组的均值向量 $E(X) = 0$,协方差矩阵 $D(X) = \Sigma$ ,假设
$$
\bf{X= S+N}
$$
其中$\bf{S}$和$\bf{N}$分别指图像中的信号和噪声,且两者不相关。
设 $\Sigma_S$ 和 $\Sigma_N$ 分别为$\bf{S}$和$\bf{N}$的协方差矩阵。这里假设噪声为加性噪声,则噪声比例可表示为:
$$
\bf{Var{N }/Var{X }}
$$
MNF 变换是一种线性变换,则有
$$
\bf{Z_i= a_i^TX, i =1,\cdots, p}
$$
$\bf{Z_i}$ 的噪声比例在所有正交于$\bf{Z_j}(j= 1,\cdots,i-1)$ 的成分中最大,将 $a_i$标准化,
$$
\bf{a_i^T\Sigma a_i = 1}
$$
由此,MNF变换表示为:
$$
\bf{Z= A^TX}
$$
式中,线性变换系数矩阵 $\bf{A=[a_1,a_2,\cdots, a_p]}$为矩阵 $\bf{\Sigma^{-1} \Sigma_N}$的特征向量矩阵,则有
$$
\bf{\Sigma^{-1} \Sigma_N}A = \Lambda A
$$
式中,对角线矩阵 $\Lambda$ 为特征值矩阵,第$i$个元素为特征值 $\lambda_i$,对应成分的噪声比例为
$$
\bf{ \frac {Var{a_i^TN }} {Var{a_i^TZ }} = \frac {a_i^T\Sigma_N a_i} {a_i^T\Sigma a_i} }
$$
MNF 变换最后变换结果的成分按照信噪比的大小排序。
3.2.3 其他常见变换
其他常见的变换包含 最小/最大自相关因子分析(minimum/maximum autocorrelation factor, MAF)、 噪声调整的主成分分析(NPCA) 、 典型相关分析(CCA)、 独立成分分析(independent compnent analysis, ICA)、 投影寻踪(projection pursuit, PP) 、 非负矩阵分解 和 非线性主成分分析(Kernel PCA, KPCA)等。
这些方法都各有其局限性和适用范围,需要根据数据质量和不同的应用需要选择适宜的方法。
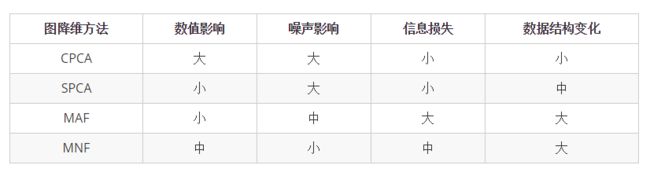
通过对常用的 CPCA、SPCA、MAF 和MNF 的优缺点进行总结,比较在目标探测的高光谱数据降维中的方法,得到下表性能分析:
可以由表总结为:
- CPCA 的优势在于信息损失小,变换后数据结构变化小,但是该方法受数值和噪声影响大;
- SPCA的优势在于受数值影响小,且在信息保留和数据结构保留保持两方面也不错,但该方法受噪声影响大;
- MNF 受数值和噪声影响小,同时信息损失小,但变换后数据结构影响很大;
- MAF 性能最差,不适用于目标探测中的高光谱数据降维
4.高光谱图像混合像元
遥感器所获取的地面反射或发射光谱信号是以 像元(pixel) 为单位记录的。由于高光谱成像光谱仪在获取大量波段时,会导致其每个波段的辐射信号较弱,为了提高信噪比、保证图像质量,就需要保证一定角度的瞬时视场角(IFOV),因此,相比全色和多光谱图像,高光谱图像的空间分辨率低,使得混合像元的问题尤为突出。
所以高光谱图像无法利用传统的图像空间信息进行分析的方法,而是利用其上百个波段丰富的光谱信息,从光谱维来挖掘图像的信息。
4.1 非线性光谱混合模型和线性光谱混合模型
物体的混合和物理分布的空间尺度决定了非线性的程度,大尺度的光谱混合完全可以被看作是一种线性混合,二小尺度的内部无核混合是非线性的。在高光谱应用中,利用非线性模型计算出的结果比线性模型计算出的结果要好,但是其需要输入众多的参数,这个实际的应用带来了困难。
非线性模型
- Hapke 混合光谱模型
- K-M(KUBELK-MUNK) 混合光谱理论模型
- 基于辐射通道密度理论的植被、土壤光谱混合模型
- SAIL 模型
- PROSPECT 模型和PROSAIL 模型
线性模型(LSMM)
当入射光在地物之间不存在多次散射时,在一定IFOV内所形成的混合像元可以通过线性混合模型(LSMM)进行描述。
4.2 光谱解混
解决混合像元问题的过程称为混合像元分解或光谱解混,就是根据遥感图像提供的信息判断每个混合像元是由哪些纯像元以怎样的方式混合的。但是,严格意义上的纯像元实际是不存在的,所以在进行解混时,通常是用图像中包含某种比例很高特征地物的像元代替纯像元。这些代替纯像元的近似纯像元,被称为端元。
线性光谱解混是利用LSMM 将遥感图像$\bf{X}$ 中每个混合像元分解成其端元和对应丰度,从而得到端元矩阵 $\bf{E}$ 和 丰度矩阵(即所占比例) $\bf{A}$ 的过程。即
$$
\bf{X_{L \times n} = E_{L \times m} A_{m \times n} + \epsilon _{L \times n}}
$$
基本工作分两步:端元提取,即确定$\bf{E}$,丰度反演,即确定 $\bf{A}$。
- 确定端元数目,在少数波段的多光谱图像中可使用PCA 根据协方差特征值的大小确定;在高光谱中使用Neyman-Pearson 探测理论的特征阈值分析分析方法确定,(确定数目中还需要对噪声进行评估,可采用光谱维去相关(SSDC)法);
- 端元提取:MaxV 方法直接用于端元提取,N-FINDER 方法需先降维再提取端元,采用降维时,提取效果:$MaxV>MNF>MAF>CPCA>SPCA$ ;
- 端元光谱变异性:由于非线性因素的影响,端元的光谱存在变异性,即同一类型存在多种端元,这也是线性光谱解混误差的主要因素之一。混合像元以及端元的光谱变异性,都是对客观事物的不确定性描述,可用模糊子集和模糊测度的思想来解决;
常用的端元提取方法还有:
- 纯像元指数(pure pixel index, PPI) 算法;
- 改进的快速迭代PPI(faster iterative PPI, FIPPI) 算法;
- 内部最大体积(N-FINDER)算法;
- 顶点成分分析(vertex component analysis,VCA) 算法;
- 基于最大距离(maximum distance, MaxD) 算法;
- 基于最大体积(maximum volume, MaxV)算法;
- 定量化独立成分(ICA)及其衍生算法等。
当得到端元矩阵 $\bf{E}$ 后,就要通过丰度反演求解高光谱图像中每个像元里各个端元所占比例,即求 丰度矩阵$\bf{A}$ 的过程。
常用的方法有:
- 最小二乘法(LS):
- 无约束(UCLS)
- "和为1"约束(SCLS)
- “非负”约束(NCLS)
- 全约束(FCLS)
- 滤波向量(FV)法
- 迭代光谱混合分析(ISMA)法等
5.高光谱遥感数据监督分类
高光谱图像数据将地物光谱信息和图像信息融为一体,其数据具有几何空间、光谱特征空间两类表达方式。
几何空间:直观表达每个像元在图像中的空间位置以及它周边像元之间的相互关系,为高光谱图像处理提供空间信息。
光谱特征空间: 高光谱遥感图像每个像元对应着多个成像波段的反射值。近似连续的光谱曲线表示为一个$N$维向量,向量在不同波段值的变化反映了其代表的目标的辐射光谱信息,其优势是特征维度的变化和扩展性。我们处理将高光谱像元作为高维特征空间的数据点,根据数据的统计特性来建立分类模型,但是它的弱点是无法表达像元间的几何位置关系。
监督分类常用于高光谱图像数据的定量分析,其主要流程是:首先,利用分类器对已知类别机器对应的训练样本进行学习,获取各图像上各类别像元的分类特征;然后,选择适当的分类判据,根据分类的决策准则进行分类。
一般按以下步骤进行:
- 高光谱数据选择。
- 图像的预处理。即几何配准、校正等,确保获取正确光谱和几何信息。
- 确定地物种类。即根据提取的训练数据特征确定分类类别。
- 选择训练样本。
- 特征提取和特征选择。选择各类地物可区分性最强的特征从而提高分类精度。
- 选择合适的分类方法进行分类。
- 分类后处理。传统基于像元分类方法分类后可能存在大量噪声及孤立像元,根据地物的连续性,利用主成分滤波等方法减少该因素影响,从蹄提高分类精度。
- 分类结果评价。根据已知类别的测试数据类别与分类结果比较,确认分类的精度与可靠性。
5.1 基于光谱特征空间分类
基于光谱特征空间的高光谱图像分类方法主要是建立在对高光谱图像光谱特征提取和变换的基础上,分为两种思路:一种是基于地物物理光学性质的光谱曲线来进行地物识别,代表性方法是光谱特征匹配方法;另一种是基于特征空间的分类方法,主要利用数据的统计特征来建立分类模型,主要方法有传统的遥感分类方法以及神经网络,支持向量机等复杂的图像分类方法。
5.1.1 光谱特征匹配分类方法
基于光谱曲线进行分类识别是利用光谱库中已知的光谱数据,采用匹配的算法来识别图像中地面覆盖类型。这种匹配既可以是全谱段范围内比较,也可以是感兴趣波段的光谱比较。
基于光谱间最小距离的匹配算法是在计算未知光谱与参考光谱距离后,再根据最最小二乘原则进行匹配的分类方法。该方法对噪声敏感,所以匹配前需要去噪预处理。
光谱角度填图(spectral angle mapping, SAM)方法 把光谱看作是光谱空间的多维矢量,计算两光谱向量的广义夹角,夹角越小,光谱越相似,最终根据相似性阈值对未知像元光谱进行分类。SAM 方法的显著特征是夹角值与光谱向量模无关,只比较光谱在形状上的相似性,这也是SAM方法与前者的区别与优势。
高光谱图像的光谱波段间隐含这特定的物理含义,光谱曲线的形状特征是地物内在物理化学性质的外在反映。
5.1.2 遥感图像统计模型分类方法
基于统计的极大似然分类是传统遥感图像分类中应用最广泛的分类方法,在极大似然分类器中,首先为简化分类过程,假设高光谱图像每类地物的概率密度都服从多维正态分布,然后利用分类训练样本分别对统计参数进行估计获得其概率密度函数,最后利用Bayes 公式将最大似然概率公式变为
$$
p(x|w_i)p(w_i) \geq p(x|w_j)p(w_j)
$$
式中, $p(w_i)$和 $p(w_j)$ 分别是类$i$与类$j$的先验概率分布,实际中由于无法估计,假设其相等。所以在实际分类过程中,将各像元划分到其属于图像上不同类别的概率中较大的那一类中去。
不足:要想获得好的效果,统计参数的估计变得十分重要;为了获得可靠的参数,每个类别必须有足够的训练样本,这对于上百个波段的高光谱图像是很困难的。
5.1.3 高光谱图像神经网络的方法
后面结合深度学习最新知识再详细介绍。
不足:高光谱图像分类时,经常遇到“同物异谱”想象,这使得神经网络的分类算法难于收敛,严重降低分类精度。
5.1.4 高光谱图像支持向量机的方法
支持向量机方法用于高光谱图像分类的优点是能够直接对高维数据处理,不必经过降维处理,而采用全部波段进行分类,保证了光谱信息的充分性。
原始SVM 算法是二分类器,在高光谱图像的多分类以及精细分类中,采用多个SVM 组合或级联的方式实现多分类。
5.2 几何空间与光谱特征空间结合的高光谱图像分类
基于光谱特征空间的高光谱图像分类方法是将高光谱数据作为一种无序的待聚类数据集合,没考虑像元点的几何空间特征,综合高光谱图像的几何空间特征和光谱特征空间进行分类,能够有效提高分类精度。
5.2.1 基于同质地物提取的高光谱图像分类方法(ECHO)
前提:图像空间分辨率较高(优于5m),常用实验数据集如AVIRIS Data 大约20m左右
主要思想:首先将图像划分为不同的图像对象,图像对象为形状与光谱特征具有相似性的同质区域;对于没有划入同质区域的像元利用极大似然分类器对它们进行分类最终获取分类结果。
5.2.2 纹理信息辅助下的高光谱图像分类
利用灰度共生矩阵进行纹理统计。
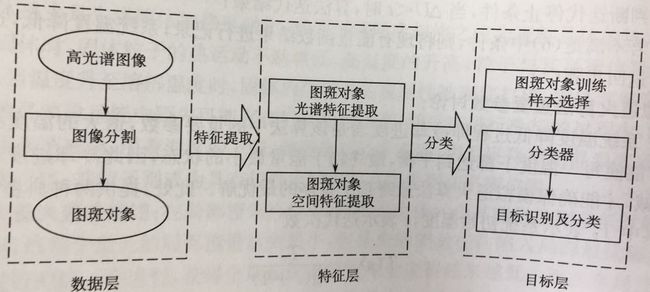
5.3 面向对象的高光谱遥感图像分类
面向对象分类的特点即分类的最基本对象从像元转换到图像对象。分类的核心是高光谱图像的分割,在这个阶段应该结合光谱信息和空间信息。
上图是面向对象的高光谱图像分类框架。
5.4 高光谱图像的分类精度评价
5.4.1 误差矩阵
误差矩阵的主体是一个 $k \times k$ 的方阵,其中列为地面参考验证信息,行为分类结果,矩阵的对角元表示被分到正确类别的像元个数,对角线以外的元素表示错分的误差。
其中,生产者精度(PA)
$$
PA_i = \frac{x_{i,i}}{x_{+i}}
$$
用户精度(UA)
$$
UA_i = \frac{x_{i,i}}{x_{i+}}
$$
5.4.2 漏分误差和多分误差
漏分误差(OE)是指类别$i$在误差矩阵中,有多少被错误分到了其他类别,类别$i$的漏分误差
$$
OE_i =1- \frac{x_{i,i}}{x_{+i}}
$$
多分误差(CE)是将其他类别像元错误划分到$i$类中,某类别$i$的多分误差为
$$
CE_i =1- \frac{x_{i,i}}{x_{i+}}
$$
5.4.3 Kappa 分析
Kappa 分析是一种定量评价遥感分类图与参考数据之间一致性或精度的方法,能识别整体图像的分类误差性。
$$
Kappa = \frac{总体精度-期望精度}{1-期望精度}
$$
计算得到
$$
Kappa = \frac {N \sum_{i=1}^kx_{i,i} - \sum_{i=1}^k(x_{i+} \times x_{+i})} {N^2 - \sum_{i=1}^k(x_{i+} \times x_{+i}) }
$$
6.高光谱图像非监督分类
高光谱图像的非监督分类算法还是采用传统遥感中的非监督方法,如 K-means 算法、ISODATA 算法、FCM 算法等算法以及它们的优化算法。
高光谱图像的非监督分类使用过程中需要注意这几个问题:
- 高光谱图像的波段众多,在自学习中会产生大量冗余,分类前进行特征提取和选择有利于提高自学习过程效率;
- 可以充分利用高光谱图像中端元提取、光谱分析等手段获得较精确的类别初值,辅助非监督分类;
- 选择非相似性度量时,需要充分考虑地物光谱特征,适当选择;
- 利用搜索算法求解非监督分类目标函数时,尝试利用全局搜索算法代替局部搜索算法提高非监督分类精度。