桥梁振动信号的预处理
桥梁振动信号是指布设在桥梁各处的传感器,将收集到各通道的信号经过放大器或变换器转化后,再由被数据采集仪采集并集中后的信号。这种序列的信号转换过程中会发生数次的信号转换过程。在此数据转换和传输的过程中,由于内部及外部各种影响因素的作用下,最后在釆集器所采集到的数据必然夹杂着许多不需要或存在问题的信号成分。因此,在使用所采集得到的数据前,必须要对采集的信号数据进行初步信号预处理,以修正波形的畸变,删除混杂在信号中的一些噪声和干扰,削弱信号中的多余内容,最终使使得大家所感兴趣的内容还原于大家的视野。
一、遗漏异常数据处理及信号合并
1 遗漏异常数据处理
在实际测量的数据中得到的测量数据通过是非常巨大的,在连续的数据采集过程中有可能会出现异常值,包括零值,空值或在某一时间范围内数据无变化,或是超出量程而无数据等各种异常情况。对这些异常数据的对将来的数据挖掘工作会产生很大的影响,所以为了提高数据质量,需要对这些异常信号行简单的判断和处理。具体为:
(1)零值判断。首先判断此零值振动信号是否为异常数据。有些时候实测数据恰好为零,此时不能被判定为异常数据,需要把这些正常的数据先排除了;
(2)空值处理。对于空值,通常采取用两个相邻值的平均值替换,或用最近的一个值替换。
(3)不合理数据处理。当某个测量值与其它桥梁数值有明显的差异时,就认为此值为不合理的异常值。在这种情况下,可采用副除粗差的方法来处理。剔除异常数据常用的几种方法:3
准则、肖维准则、格拉布斯准则等。
2 振动信号的合并及时间尺度统一
桥梁监测系统中的数据是由温度、加速度传感器、位移、应变等多种传感器釆集到的。由于传感器的工作原理及仪器的工作性能不同,各传感器的采样频率不能做到完全一致。然而,对于桥梁监测而言,需要了解同一时期各个部分的结构响应,才能再清楚地了解整体结构的力学性能。因此,在后期数据处理时,就需要对各通道的数据的时间尺度进行统一。
同时,由于桥梁上所布置的传感器的数量庞大,分布于桥梁的各个位置,通常要通过数个采集器分别采集数据,有可能会导致得到的采集数据的时间轴并不统一,因此,也需要对采集数据的时间尺度进行统一。
各种数型的传感器由于受到采集设备和数据类型等的限制,无法将所有设备采集到的数据统一放在一个文件中。如果只需要查看某一个传感器的数据时,并不需要进行数据合并;然而,当需要多个变量的数据分析或全桥响应分析时,数据合并就显得十分得要了。例如需要对某一实桥的监测系统中的加速度、温度和湿度等传感器收集到的数据进行测量和分析,其中加速度传感器采样频率为每五十分之一秒采集一次;而温度和湿度传感器每1分钟采集1次,当各种不同的采集时间间隔的数据需要进行一起分析时,就需要对多种不同的时间间隔数据进行合并处理。
二 振动信号消除趋势项
桥梁结构的振动过程中所采集到振动信号会隐藏着一些环境的干扰信号,比如通过放大器受温度影响会产生变化而引起测量的零点漂移、传感器的工作频率外的低频性能不稳定以及周围环境对传感器的干扰。在以上各种影响因素的作用下经常使得数据偏离基线,还有可能会导致偏离的基线会随时间变化,这个偏离被称为信号的趋势项。由于数据分析结果的正确性直接受趋势项的影响,所以需要消除趋势项以实现数据的预处理。目前来说,比较经常使得的消除趋势项的方法是多项式最小二乘法。
假定采集得到的振动数据为{xk}(k=1,2,3,4,5,…,n).由于采样数据是在等时间
间隔采用的,为了简化其在文中的标识,使采样时间间隔□t=1,固此多项式函数为:
(1)
需确定函数
的待定系数
,使得其与离散数据xk的误差平方和最小,即可得到下式:
(2)
要使得上式满足五有极值的条件为
(3)
依次取E对ai求偏导,可以产生一个m+1元线性方程组:
(4)
利用以上解方程组,求出m+1个待定系数
。其中,m为设定的多项式阶次,其取值的范围为
。
当m=0时求得的趋势项为常数,如下式所示:
(5)
求解方程可以得到下式:
(6)
根据上文,可以看出,当m=0时的趋势项为信号采样数据的算术平均值。因此,
消除常数趋势项的计算公式为:
(7)
当m=l为线性趋势项,可以得到下式:
(8)
求解方程可以得到下式:
(9)
消除线性趋势项的计算公式可以用下式来表达:
(10)
时为曲线趋势项。实际应用中,对于采样到的振动数据信号进行多项势趋势项处理时我们通常取W=1~3。
下文中以实际数据处理算例来阐述消除趋势项的应用。
例1
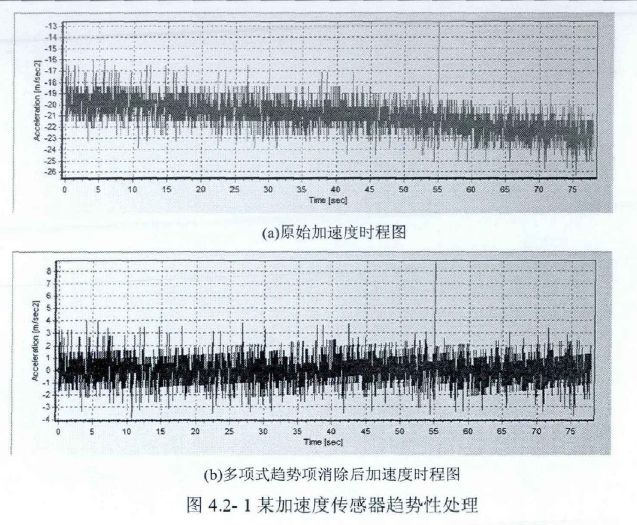
本文取某桥梁在随机汽车荷载作用下实测的桥面竖向振动时程曲线为例。由采集系统实际采集到的加速度时程曲线如图4-l(a)所示。由图中可以发现实测数据飘动明显。本文釆有多项式趋势项对采集到的实际数据进行处理,得到修正后的加速度时程曲线,如4.2-1(b)所示。
例2
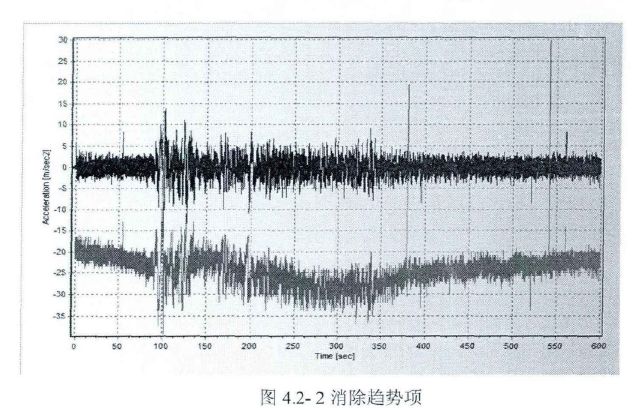
4.2-2为某大跨悬索桥模拟地震振动台试验中,某工况的地震作用下主塔顶纵桥向的加速度时程曲线。由实际的试验过程可以知道,在振动台激励前和激励结束后,塔顶的实测加速度应趋近于0,因此,可以判断此实测曲线包含了测量误差引起的趋势项。图4-3中灰色曲线就是过消除其趋势项后获得的比较理想的加速度响应时程曲线。
《非本人原创,由本人整理,以技术会友,广交天下朋友》