1.1图的思维导图
1.2 图结构学习体会
1.深度遍历算法
深度优先遍历,又简称为DFS。思想是不放过任何一个死角。在图的遍历中就是从图的某个顶点v出发,访问此顶点,然后从v的未被访问过的邻接点出发深度优先遍历图,直至图中的所有和v有路径相通的顶点都被访问到(对于连通图来讲)。
2.广度遍历算法
广度优先搜索的思想:
① 访问顶点vi ;
② 访问vi 的所有未被访问的邻接点w1 ,w2 , …wk ;
③ 依次从这些邻接点(在步骤②中访问的顶点)出发,访问它们的所有未被访问的邻接点; 依此类推,直到图中所有访问过的顶点的邻接点都被访问;
3.Prim算法
普里姆算法(Prim算法),图论中的一种算法,可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中,不但包括了连通图里的所有顶点(英语:Vertex (graph theory)),且其所有边的权值之和亦为最小
4.Kruscal算法
这个算法是相对于Prim算法的另外一个算法,这个算法主要的应用场景是对于稀疏图非常好用,因为Karuscal算法是根据边来计算的,每次添加一个最短的边。
首先对所有边进行一次排序,然后每次找到最短的边,假如这个边的两个点不属于同一个子树,就加入进来,如果属于同一棵子树,就找下一个边
5.Dijkstra算法
Dijkstra算法是典型的最短路径算法。它的关键思想是以起始点为中心,向外一层层扩散,直到扩展到终点为止。Dijkstra算法能够得出最短路径的最优解,不过它需要遍历计算的节点相当多,所以效率不高
6.拓扑排序算法
对一个有向无环图(Directed Acyclic Graph简称DAG)G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边(u,v)∈E(G),则u在线性序列中出现在v之前。
2.PTA实验作业
1.7-1 图着色问题
(1)设计思路:直先利用图的遍历来判断颜色是否相等。
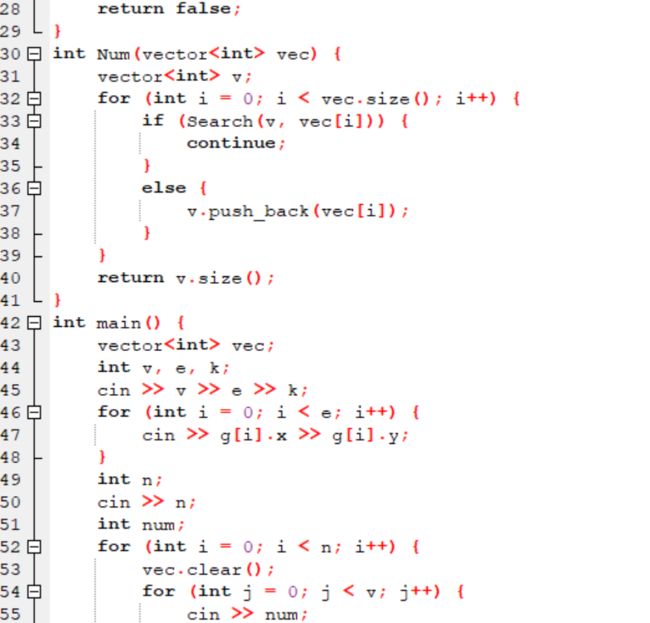
(2)代码截图
(2)PTA提交列表
第一次是由于用C++写,然而提交时没有提交C++的,第二次是由于输出时格式不正确
2.7-2 排座位
(1)代码
#include
#include
using namespace std;
int fir[105][105];
int vis[105][105];
int n,m,k,tou;
void dfs(int x,int y)
{
if(tou==1)
return;
int i;
for(i=1;i<=n;i++)
{
if(vis[x][i]==1)
continue;
if(fir[x][i]==1)
{
if(i==y)
{
tou=1;
return;
}
else
{
vis[x][i]=1;
vis[i][x]=1;
dfs(i,y);
}
}
}
}
int main()
{ int u,v,w,x,y;
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
fir[i][j]=0;
}
}
while(m--)
{
scanf("%d%d%d",&u,&v,&w);
fir[u][v]=fir[v][u]=w;
}
while(k--)
{
scanf("%d%d",&x,&y);
for(int i=0;i
for(int j=0;j
vis[i][j]=0;
}
}
tou=0;
if(fir[x][y]==1)
{
printf("No problem\n");
continue;
}
vis[x][y]=1;vis[y][x]=1;
dfs(x,y);
if(fir[x][y]==-1)
{
if(tou==1)
printf("OK but...\n");
else
printf("No way\n");
}
else
{
if(tou==1)
printf("No problem\n");
else
printf("OK\n");
}
}
}
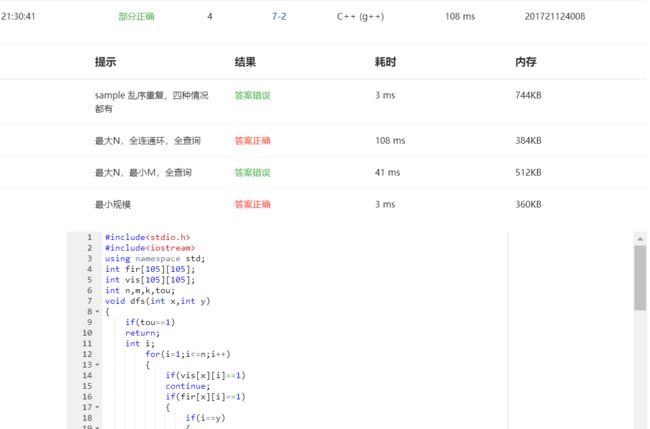
(2)PTA提交列表
部分正确是由于思考时漏了考虑k!=0时,并且fir[x][y]!=-1时的问题。
3.7-4 公路村村通
(1)本题代码来自网络
(2)代码
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define mod 1000000007
const int INF = 0x3f3f3f3f;
typedef long long ll;
const int maxn = 1050;
using namespace std;
int mp[maxn][maxn];
bool vis[maxn];
int dist[maxn];
int n, m;
int findmin()
{
int v = -1, minlen = INF;
for(int i = 1; i <= n; i++)
{
if(!vis[i] && dist[i] < minlen)
{
v = i;
minlen = dist[i];
}
}
return v;
}
int prim(int star)
{
vis[star] = true;
int cnt = 0, sumlen = 0;
for(int i = 1; i <= n; i++)
{
dist[i] = mp[star][i];
}
while(1)
{
int v = findmin();
if(-1 == v)
break;
vis[v] = true;
cnt++;
sumlen += dist[v];
for(int i = 1; i <= n; i++)
{
if(!vis[i] && mp[v][i] < dist[i])
{
dist[i] = mp[v][i];
}
}
}
if(n-1 == cnt)
return sumlen;
else
return -1;
}
int main()
{
memset(vis, 0, sizeof(vis));
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= n; j++)
{
if(i == j)
{
mp[i][j] = 0;
}
else
{
mp[i][j] = INF;
}
}
}
for(int i = 0; i < m; i++)
{
int t1, t2, t3;
scanf("%d%d%d", &t1, &t2, &t3);
mp[t1][t2] = t3;
mp[t2][t1] = t3;
}
int k = prim(1);
printf("%d\n", k);
return 0;
}
(3)PTA提交列表
3.PTA排名