最近点对问题,就是在一个点集中找到最近的一对点的距离。
先看一道例题
AcWing119
在题解的帮助下,我终于A了此题。
题目大意就是有n个特工和n个核电站,求最近的任意一个特工到任意一个核电站的距离。
首先我们只要将点分为两组,同组的点之间距离为无穷大,就可以将本题转换为最近点对问题。
最近点对问题如何解呢?
第一时间想到的是n2的暴力,但无疑是要超时的。
于是我们需要用分治来优化一下。
首先在一般情况下,最近两个点的横坐标的差是较小的,我们可以对于横坐标进行分治。
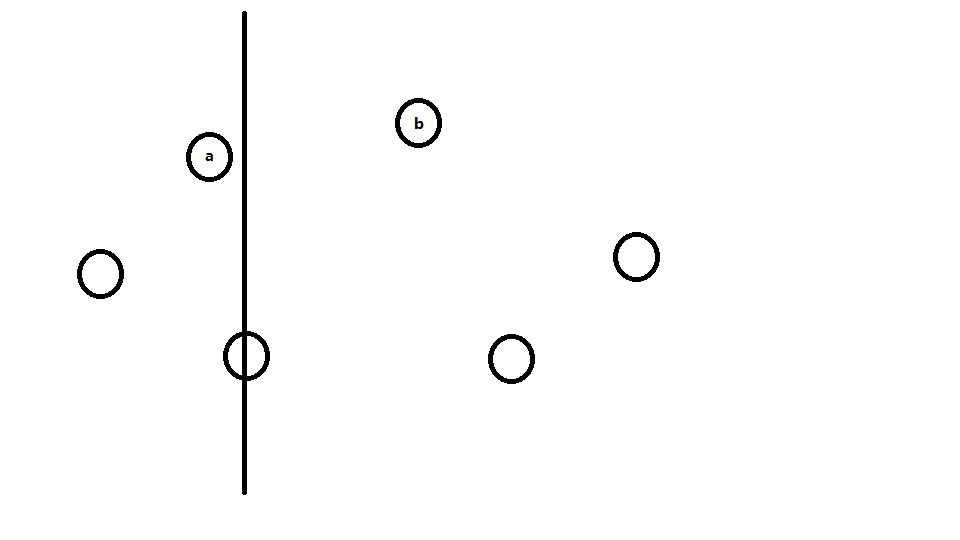
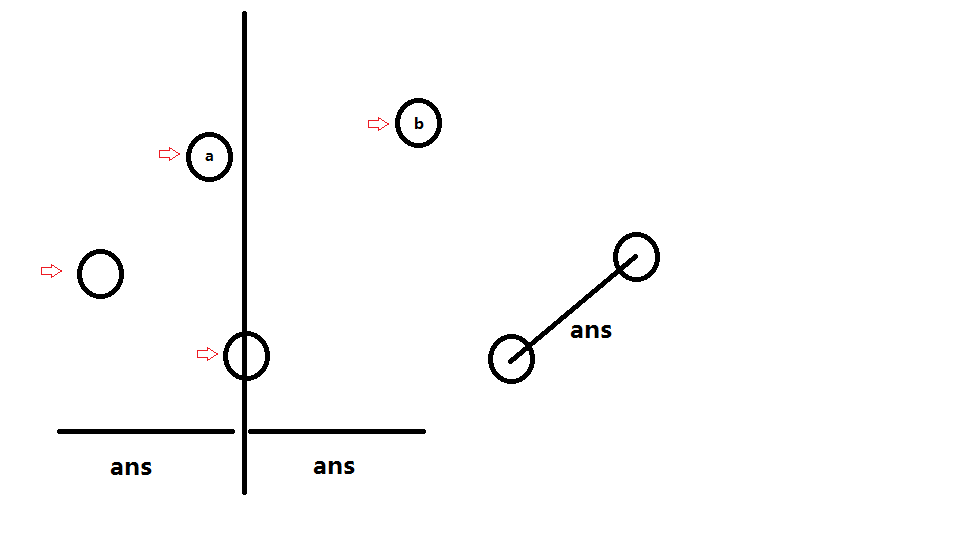
如图,以横坐标为第一关键字排序后,将所有点分成两部分(至于中间那个随便分到哪块)。
很显然最短距离是在左块的最短距离和右块的最短距离,当然也可能不同块的点的距离,比如说图中的ab。
前两种都是非常方便实现的,只需要不断分治就好。麻烦的是第三种情况。
我们可以先将前两种的最小值ans求出,以横坐标和中间点差小于等于ans的才可能是第三种情况。
于是我们只需要求这些点之中最短距离。
对于这些点我们可以直接用暴力做,一般情况下应该不会很大。
当然,如果纵坐标的距离大于ans,也是不可能是最短距离的。
sort(b + 1, b + cnt + 1, cmp2);
rep(i, 1, cnt)
rep(j, i + 1, cnt){
if(b[j].y >= b[i].y + ans) break;
ans = min(ans, dist(b[i], b[j]));
}
可以将纵坐标为第一关键字排序,进行剪枝。
放上我错了好几次的代码
1 #include2 #include 3 #include 4 #include 5 #include 6 #include 7 #define rep(x, l, r) for(int x = l; x <= r; x++) 8 #define repd(x, r, l) for(int x = r; x >= l; x--) 9 #define clr(x, y) memset(x, y, sizeof(x)) 10 #define all(x) x.begin(), x.end() 11 #define pb push_back 12 #define mp make_pair 13 #define MAXN 200005 14 #define fi first 15 #define se second 16 #define SZ(x) ((int)x.size()) 17 using namespace std; 18 typedef long long ll; 19 typedef vector<int> vi; 20 typedef pair<int, int> pii; 21 const int INF = 1 << 30; 22 const int p = 1000000009; 23 int lowbit(int x){ return x & (-x);} 24 int fast_power(int a, int b){ int x; for(x = 1; b; b >>= 1){ if(b & 1) x = 1ll * x * a % p; a = 1ll * a * a % p;} return x % p;} 25 26 int n; 27 struct node{ 28 double x, y; 29 bool col; 30 }a[MAXN], b[MAXN]; 31 32 bool cmp1(node a, node b){ 33 if(a.x == b.x) return a.y < b.y; 34 return a.x < b.x; 35 } 36 37 bool cmp2(node a, node b){ 38 if(a.y == b.y) return a.x < b.x; 39 return a.y < b.y; 40 } 41 42 double dist(node a, node b){ 43 if(a.col == b.col) return INF; 44 return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y)); 45 } 46 47 double work(int l, int r){ 48 if(l == r) return INF; 49 if(l == r - 1) return dist(a[l], a[r]); 50 int mid = (l + r) >> 1; 51 double ans = min(work(l, mid), work(mid + 1, r)); 52 int cnt = 0; 53 rep(i, l, r) 54 if(a[i].x >= a[mid].x - ans && a[i].x <= a[mid].x + ans) b[++cnt] = a[i]; 55 sort(b + 1, b + cnt + 1, cmp2); 56 rep(i, 1, cnt) 57 rep(j, i + 1, cnt){ 58 if(b[j].y >= b[i].y + ans) break; 59 ans = min(ans, dist(b[i], b[j])); 60 } 61 return ans; 62 } 63 64 int main(){ 65 int t; 66 scanf("%d", &t); 67 while(t--){ 68 scanf("%d", &n); 69 rep(i, 1, n){ 70 scanf("%lf%lf", &a[i].x, &a[i].y); 71 a[i].col = 0; 72 } 73 rep(i, n + 1, 2 * n){ 74 scanf("%lf%lf", &a[i].x, &a[i].y); 75 a[i].col = 1; 76 } 77 n *= 2; 78 sort(a + 1, a + n + 1, cmp1); 79 double ans = work(1, n); 80 printf("%.3f\n", ans); 81 } 82 return 0; 83 }