时隔两月开始继续储备机器学习的知识,监督学习已经告一段落,非监督学习从聚类开始。
非监督学习与监督学习最大的区别在于目标变量事先不存在,也就是说
监督学习可以做到“对于输入数据X能预测变量Y”,而非监督学习能做到的是“从数据X中能发现什么?”,比如“构成X的最佳6个数据簇都是哪些?”或者“X中哪三个特征最频繁共现?”
这就很好玩了,比如我在Udacity的第三个项目,一家批发经销商想将发货方式从每周五次减少到每周三次,简称成本,但是造成一些客户的不满意,取消了提货,带来更大亏损,项目要求是通过分析客户类别,选择合适的发货方式,达到技能降低成本又能降低客户不满意度的目的。
什么是聚类
聚类将相似的对象归到同一个簇中,几乎可以应用于所有对象,聚类的对象越相似,聚类效果越好。聚类与分类的不同之处在于分类预先知道所分的类到底是什么,而聚类则预先不知道目标,但是可以通过簇识别(cluster identification)告诉我们这些簇到底都是什么。
K-means
聚类的一种,之所以叫k-均值是因为它可以发现k个不同的簇,且每个簇的中心采用簇中所含值的均值计算而成。簇个数k是用户给定的,每一个簇通过质心来描述。
k-means的工作流程是:
- 随机确定k个初始点做为质心
- 给数据集中的每个点找距其最近的质心,并分配到该簇
- 将每个簇的质心更新为该簇所有点的平均值
- 循环上两部,直到每个点的簇分配结果不在改变为止
项目流程
载入数据集
import pandas as pd
data = pd.read_csv("customers.csv");
分析数据
显示数据的一个描述
from IPython.display import display
display(data.discrie());
分析数据是一门学问,感觉自己在这方面还需要多加练习,数据描述包含数据总数,特征,每个特征的均值,标准差,还有最小值、25%、50%、75%、最大值处的值,这些都可以很容易列出来,但是透过这些数据需要看到什么信息,如何与需求目的结合,最开始还是比较吃力的。可以先选择几个数值差异较大的样本,然后结合数据描述和需求,对数据整体有一个把控。比如在Udacity的第三个项目中,给出客户针对不同类型产品的年度采购额,分析猜测每个样本客户的类型。
三个样本客户
每个客户究竟是什么类型,这个问题困扰我好久,第一次回答我只是看那个方面采购额最大,就给它一个最近的类型,提交项目后Reviewer这样建议:
这里有一个问题, 你在讨论一个样本对某产品的采购时没有以统计数据为参考. 注意, "大量" 和 "少量" 的描述都应该相对于统计数据而言.
提示: 从data.describe()中你已经得到了均值和四分位数, 把它们利用起来.
恍然大悟,这才知道了该如何分析一份数据集,于是有了下面的回答
所以分析数据一定要结合统计数据,四分位数和均值可以看做数据的骨架,能够一定程度勾勒出数据的分布,可以通过箱线图来可视化四分位数。
分析特征相关性
特征之间通常都有相关性,可以通过用移除某个特征后的数据集构建一个监督学习模型,用其余特征预测移除的特征,对结果进行评分的方法来判断特征间的相关性。比如用决策树回归模型和R2分数来判断某个特征是否必要。
from sklearn.model_selection import train_test_split
from sklearn import tree
new_data = data.drop('Feature name', axis = 1);
X_train, X_test, y_train, y_test = train_test_split(new_data, data['Feature name'], test_size = 0.25, random_state = 50)
regressor = tree.DecisionTreeRegressor(random_state = 50).fit(X_train, y_train);
score = regressor.score(X_test, y_test)
print(score);
如果是负数,说明该特征绝对不能少,因为缺少了就无法拟合数据。如果是1,表示少了也无所谓,有一个跟它相关联的特征能代替它,如果是0到1间的其他数,则可以少,只是有一定的影响,越靠近0,影响越大。
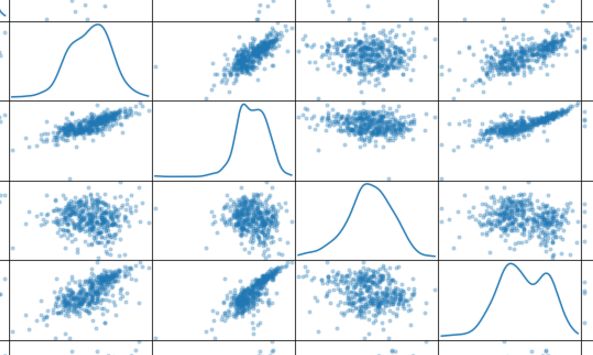
也可以通过散布矩阵(scatter matrix)来可视化特征分布,如果一个特征是必须的,则它和其他特征可能不会显示任何关系,如果不是必须的,则可能和某个特征呈线性或其他关系。
# 对于数据中的每一对特征构造一个散布矩阵
pd.tools.plotting.scatter_matrix(data, alpha = 0.3, figsize = (14,8), diagonal = 'kde');
数据预处理
(一)特征缩放
如果数据特征呈偏态分布,通常进行非线性缩放。
# 使用自然对数缩放数据
log_data = np.log(data);
# 为每一对新产生的特征制作一个散射矩阵
pd.tools.plotting.scatter_matrix(log_data, alpha = 0.3, figsize = (14,8), diagonal = 'kde');
可以发现散布矩阵变成了下图
(二)异常值检测
通常用 Tukey的定义异常值的方法检测异常值。
一个异常阶(outlier step)被定义成1.5倍的四分位距(interquartile range,IQR)。一个数据点如果某个特征包含在该特征的IQR之外的特征,那么该数据点被认定为异常点。
# 对于每一个特征,找到值异常高或者是异常低的数据点
for feature in log_data.keys():
# 计算给定特征的Q1(数据的25th分位点)
Q1 = np.percentile(log_data[feature], 25);
#计算给定特征的Q3(数据的75th分位点)
Q3 = np.percentile(log_data[feature], 75);
#使用四分位范围计算异常阶(1.5倍的四分位距)
step = (Q3 - Q1) * 1.5;
# 显示异常点
print "Data points considered outliers for the feature '{}':".format(feature)
display(log_data[~((log_data[feature] >= Q1 - step) & (log_data[feature] <= Q3 + step))])
# 可选:选择你希望移除的数据点的索引
outliers = [65, 66, 75, 154, 128];
# 如果选择了的话,移除异常点
good_data = log_data.drop(log_data.index[outliers]).reset_index(drop = True)
移除异常值需要具体情况具体考虑,但是要谨慎,因为我们需要充分理解数据,记录号移除的点以及移除原因。可以用counter来辅助寻找出现次数大于1的离群点。
from collections import Counter
print dict(Counter(['a', 'b', 'c', 'a', 'b', 'b'])) # {'b': 3, 'a': 2, 'c': 1}
(三)特征转换
特征转换主要用到主成分分析发,请查看之前介绍。
聚类
有些问题的聚类数目可能是已知的,但是我们并不能保证某个聚类的数目对这个数据是最优的,因为我们对数据的结构是不清楚的。但是我们可以通过计算每一个簇中点的轮廓系数来衡量聚类的质量。数据点的轮廓系数衡量了分配给它的簇的相似度,范围-1(不相似)到1(相似)。平均轮廓系数为我们提供了一种简单地度量聚类质量的方法。
下面代码会显示聚类数为2时的平均轮廓系数,可以修改n_clusters来得到不同聚类数目下的平均轮廓系数。
from sklearn.cluster import KMeans
clusterer = KMeans(n_clusters=2, random_state=50).fit(reduced_data);
# 预测每一个点的簇
preds = clusterer.predict(reduced_data);
# 找到聚类中心
centers = clusterer.cluster_centers_;
# 计算选择的类别的平均轮廓系数(mean silhouette coefficient)
from sklearn.metrics import silhouette_score
score = silhouette_score(reduced_data, preds);
数据恢复
如果用对数做了降维,可以用指数将数据恢复。