第五章 MATLAB 的图形和可视化功能
MATLAB 中最常用的绘图函数为 plot 。
plot 的调用格式为:
plot(x, y) 其中 x 和 y 为坐标向量。
plot 颜色与线型参数
颜色:
-
y:黄色 -
m:紫色 -
c:青色 -
r:红色 -
g:绿色 -
b:蓝色 -
w:白色 -
k:黑色
线型:
-
.:点 -
。:圆圈 -
x:叉号 +*-
-:实线 -
::点线 -
-.:点划线 -
-:虚线
图形标记
设定坐标轴
axis 函数
axis([xmin xmax ymin ymax])-
axis('auto'): 坐标系统返回自动缺省状态 -
axis('square'): 图形设置为方形 -
axis('equal'): 两个坐标因子设定成相等 -
axis('off'): 关闭坐标系统 -
axis('on'):
添加图例
subplot 函数,多幅图布局
hold 命令
若在已存在的图形窗口中用 plot 函数继续添加新的图形内容,可使用图形保持指令 hold 。发出 hold on 后,再执行 plot 函数,在保持原有图形的基础上添加新的绘制图形。hold off 关闭此功能。
函数 f(x) 曲线
绘制函数曲线的方法有很多,最常用的方法:对采样点向量 x 计算出 f(x) 的值向量,再用 plot(x, y) 函数绘制。
plot 函数一般采用等间隔采样,对绘制高频率变化的函数不够精确。
为提高精度,不能采用等步长采样,必须在变化率大的区域密集采用,以充分反映函数的实际变化规律,提高图形的真实度。
fplot 函数可自适应的对函数进行采样,更好地反映函数的变化规律。
函数格式:fplot(fname, lims, tol)
-
fname:函数名 -
lims:变量取值范围 -
tol:相对允许误差,默认2e-3
特殊坐标图形
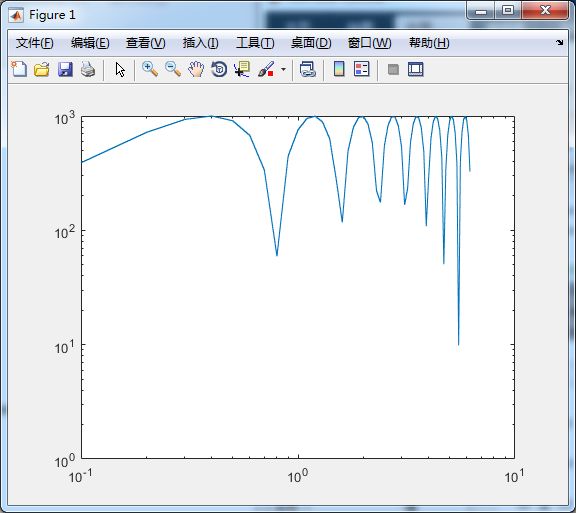
- 双对数坐标
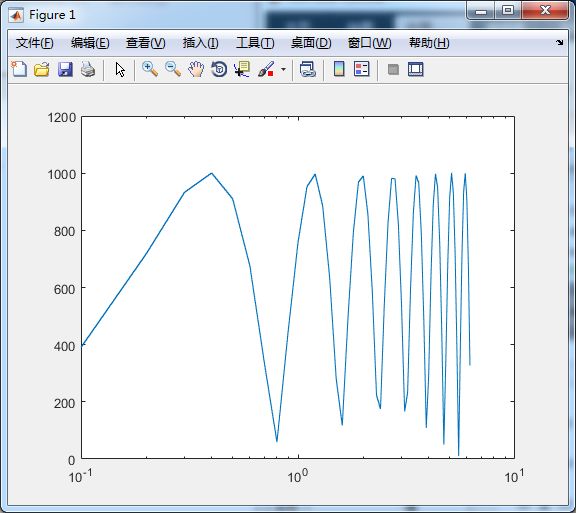
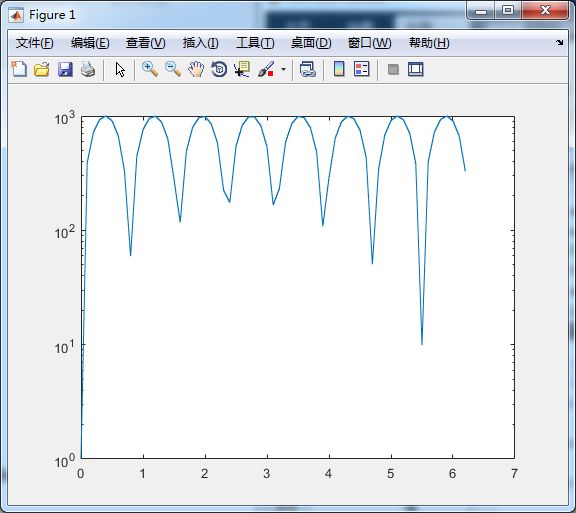
- 单对数坐标
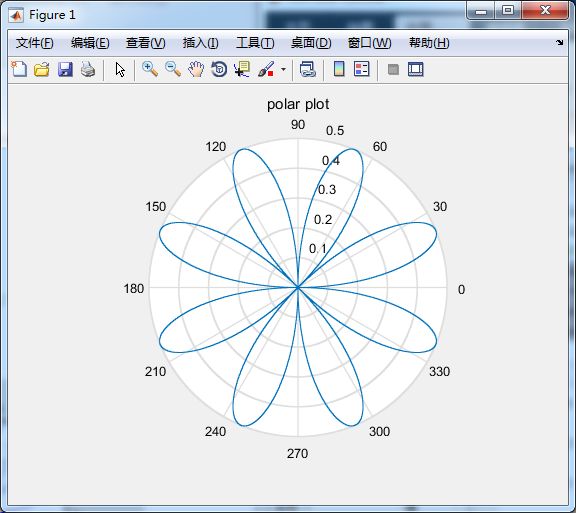
- 极坐标
- 阶梯图形
- 条形图形
二维绘图函数小结
plotfplot-
fill: 填充二维多变图形 -
polar: 极坐标图形 -
bar: 条形图 loglogsemilogxsemilogystairs-
axis: 设置坐标轴 -
clf: 清除图形窗口内容 close-
figure: 创建图形窗口 -
grid: 放置坐标网格线 -
gtext: 用鼠标放置文本 -
hold: 保持当前图形内容 subplottexttitlexlabelylabel
三维图形
plot3 函数
mesh 函数:绘制三维网格图
surf 函数:三维曲面图
代码
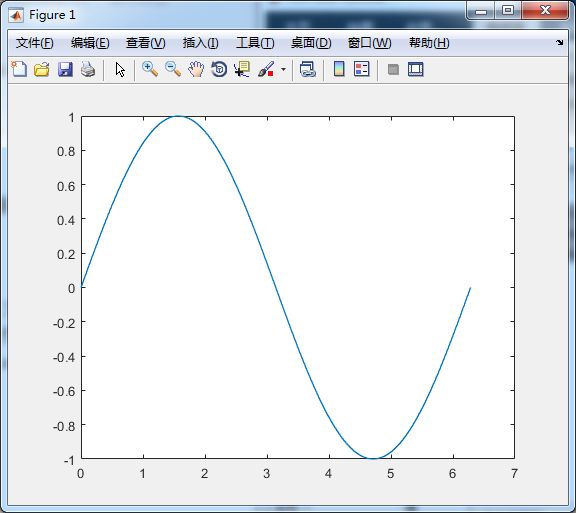
%plot函数
x = 0:pi/100:2*pi;
y = sin(x);
plot(x, y)
x = 0:pi/100:2*pi;
y1 = sin(x);
y2 = cos(x);
plot(x, y1, x, y2)
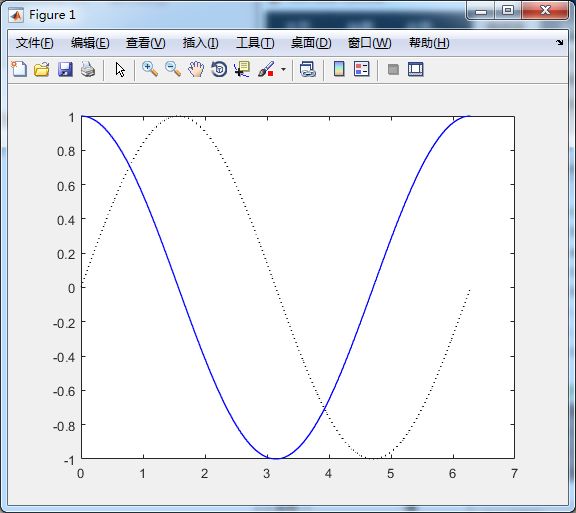
%线型与颜色
x = 0:pi/100:2*pi;
y1 = sin(x);
y2 = cos(x);
plot(x, y1, 'k:', x, y2, 'b-')
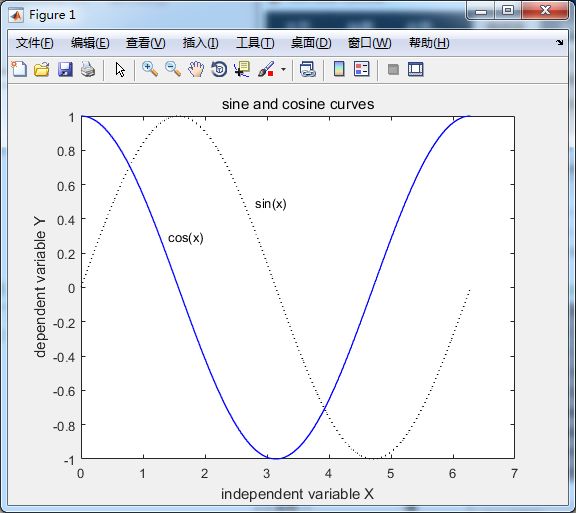
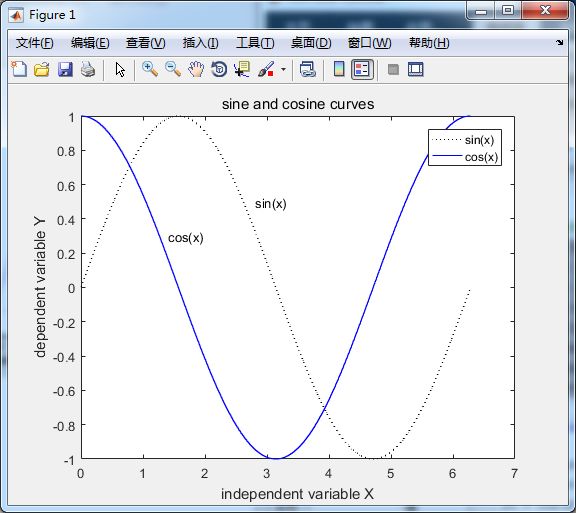
%图形标记
x = 0:pi/100:2*pi;
y1 = sin(x);
y2 = cos(x);
plot(x, y1, 'k:', x, y2, 'b-')
title('sine and cosine curves'); %标题
xlabel('independent variable X');
ylabel('dependent variable Y');
text(2.8, 0.5, 'sin(x)');
text(1.4, 0.3, 'cos(x)');
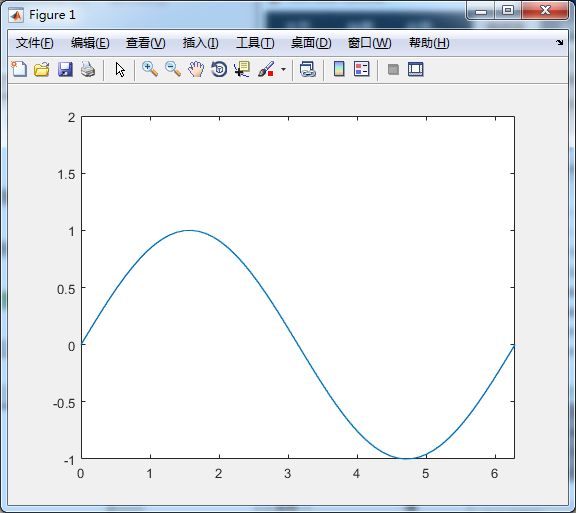
%设定坐标轴
x = linspace(0, 2*pi, 60);%生成含有60个数据元素的向量x
y = sin(x);
plot(x, y);
axis([0, 2*pi, -1, 2]); %设定坐标范围
%添加图例
x = 0:pi/100:2*pi;
y1 = sin(x);
y2 = cos(x);
plot(x, y1, 'k:', x, y2, 'b-')
title('sine and cosine curves'); %标题
xlabel('independent variable X');
ylabel('dependent variable Y');
text(2.8, 0.5, 'sin(x)');
text(1.4, 0.3, 'cos(x)');
legend('sin(x)', 'cos(x)');
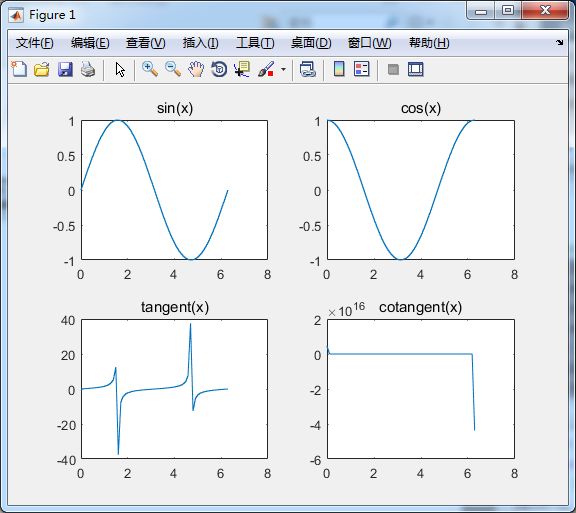
%subplot 函数
x = linspace(0, 2*pi, 60);
y = sin(x);
z = cos(x);
t = sin(x)./(cos(x)+eps);
ct = cos(x)./(sin(x)+eps);
subplot(2, 2, 1); %两行两列,第一个
plot(x, y);
title('sin(x)');
%axis([0, 2*pi, -1, 1]);
subplot(2,2,2);
plot(x, z);
title('cos(x)');
%axis([0, 2*pi, -1, 1]);
subplot(2, 2, 3);
plot(x, t);
title('tangent(x)');
%axis([0, 2*pi, -40, 40]);
subplot(2, 2, 4);
plot(x, ct);
title('cotangent(x)');
%axis([0, 2*pi, -40, 40]);
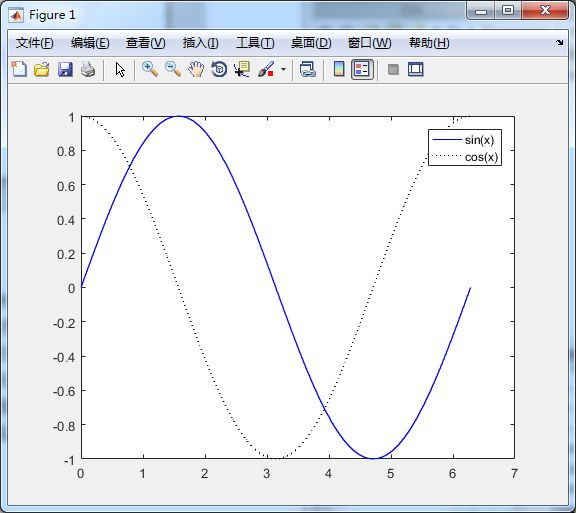
%hold命令
x = linspace(0, 2*pi, 60);
y = sin(x);
z = cos(x);
plot(x, y, 'b');
hold on;
plot(x, z, 'k:');
legend('sin(x)', 'cos(x)');
hold off
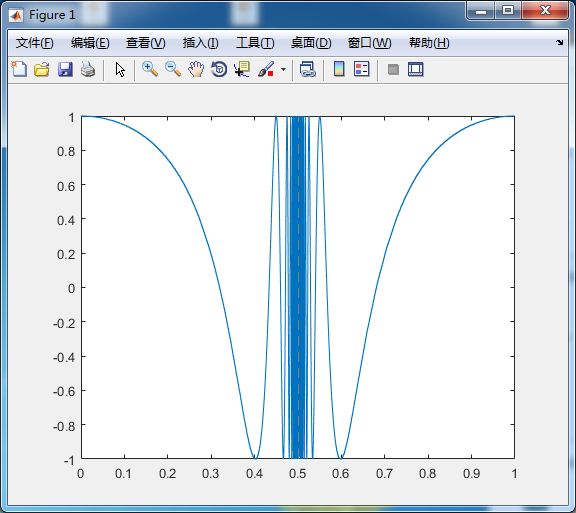
%函数f(x)曲线
fplot('sin(x)', [0 2*pi], 1e-3)
fplot('[sin(x), cos(x)]', [0 2*pi], 1e-3)
fplot(@fct, [0, 1])
%双对数坐标
x = 0:0.1:2*pi;
y = abs(1000*sin(4*x))+1
loglog(x, y);
%单对数坐标
x = 0:0.1:2*pi;
y = abs(1000*sin(4*x))+1
semilogx(x, y); %x轴为对数
semilogy(x, y); %
%极坐标图形
theta = 0:0.01:2*pi;
rho = sin(2*theta).*cos(2*theta);
polar(theta, rho);
title('polar plot');
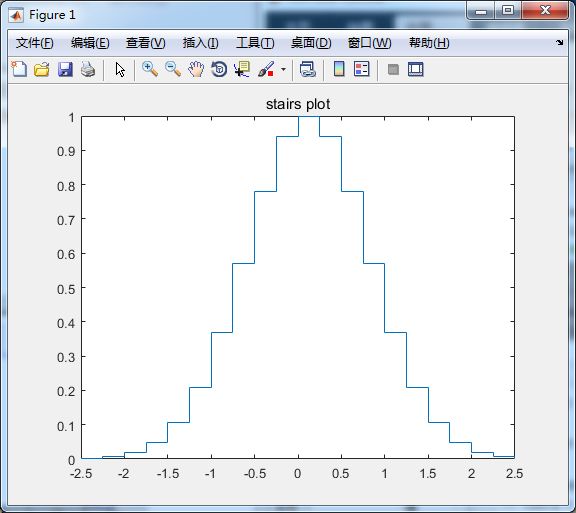
%阶梯图形
x = -2.5:0.25:2.5;
y = exp(-x.*x);
stairs(x, y);
title('stairs plot');
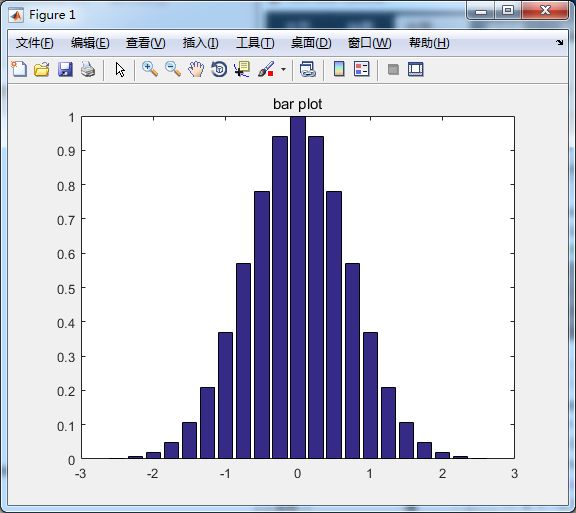
%条形图形
x = -2.5:0.25:2.5;
y = exp(-x.*x);
bar(x, y);
title('bar plot');
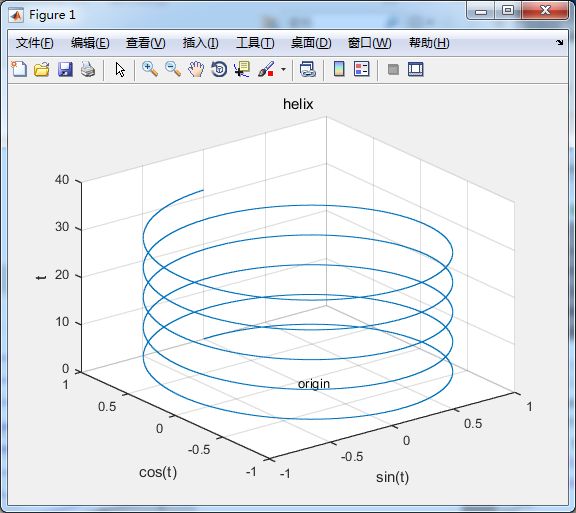
%三维图形
t = 0:pi/50:10*pi;
y1 = sin(t); y2 = cos(t);
plot3(y1, y2, t)
title('helix'), text(0, 0, 0, 'origin');
xlabel('sin(t)'), ylabel('cos(t)'), zlabel('t');
grid;
%三维网格图
x = 0:0.15:2*pi;
y = 0:0.15:2*pi;
z = sin(y')*cos(x);
mesh(x, y, z)
title('三维网格图');
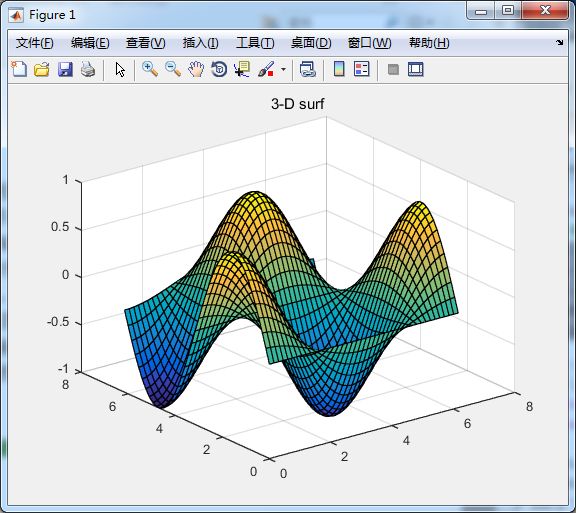
%三维曲面图
x = 0:0.15:2*pi;
y = 0:0.15:2*pi;
z = sin(y')*cos(x);
surf(x, y, z)
title('3-D surf');
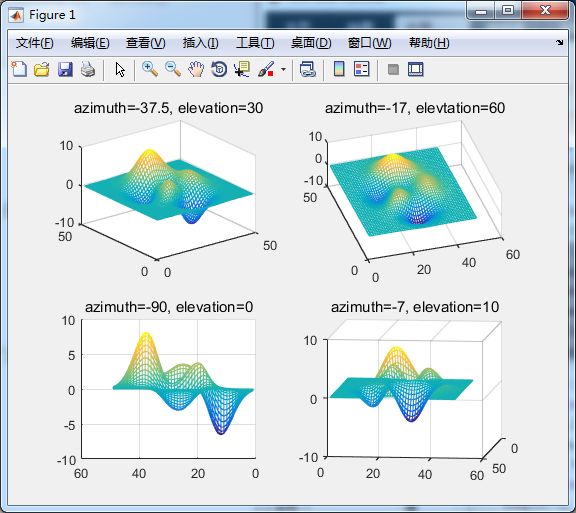
%视点
p = peaks; %peaks为系统提供多峰函数
subplot(2, 2, 1);
mesh(peaks, p);
view(-37.5, 30); %指定图1的视点
title('azimuth=-37.5, elevation=30');
subplot(2,2,2);
mesh(peaks,p);
view(-17, 60) %
title('azimuth=-17, elevtation=60');
subplot(2, 2, 3);
mesh(peaks, p);
view(-90, 0);
title('azimuth=-90, elevation=0');
subplot(2, 2, 4);
mesh(peaks, p);
view(-7, -10);
title('azimuth=-7, elevation=10');
%等高线图
hold off
[x, y, z] = peaks(30);
contour3(x, y, z, 16);
xlabel('X-axis'), ylabel('Y-axis'), zlabel('Z-axis');
title('等高线图');