CF1263F

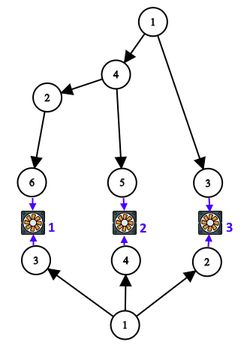
题目描述

给出一个类似这样

的图，求删掉最多的黑边使得每个特殊点和至少一个节点1连通

保证上下两棵树都存在一种dfs序使得访问特殊点的顺序为1~n

题解

设f[i][j]表示上面的树最后一个特殊点为i，j同理的最小选取数

每次加上lca-->max(i,j)+1的路径，由于题目保证了dfs顺序，所以不会出现不合法的情况

code

#include 
#include 
#include 
#include 
#include 
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define min(a,b) (ab?a:b)
using namespace std;

int a[10001][2];
int ls[5001];
int fa[2][5001][11];
int d[2][5001];
int f[1001][1001];
int n,A,B,i,j,k,l,len,ans;

void New(int x,int y)
{
    ++len;
    a[len][0]=y;
    a[len][1]=ls[x];
    ls[x]=len;
}

void dfs(int type,int t)
{
    int i;
    
    fo(i,1,10)
    fa[type][t][i]=fa[type][fa[type][t][i-1]][i-1];
    
    if (t<=n) return;
    
    for (i=ls[t]; i; i=a[i][1])
    {
        fa[type][a[i][0]][0]=t;
        d[type][a[i][0]]=d[type][t]+1;
        
        dfs(type,a[i][0]);
    }
}

void swap(int &x,int &y)
{
    int z=x;
    x=y;
    y=z;
}

int lca(int type,int x,int y)
{
    int i;
    
    if (!x)
    {
        if (!type)
        return n+1;
        else
        return n+A+1;
    }
    
    if (d[type][x]=d[type][y])
    x=fa[type][x][i];
    
    fd(i,10,0)
    if (fa[type][x][i]!=fa[type][y][i])
    x=fa[type][x][i],y=fa[type][y][i];
    
    if (x!=y)
    x=fa[type][x][0];
    
    return x;
}

int main()
{
//  freopen("f.in","r",stdin);
    
    scanf("%d",&n);
    scanf("%d",&A);
    fo(i,2,A)
    {
        scanf("%d",&j);
        New(j+n,i+n);
    }
    fo(i,1,n)
    {
        scanf("%d",&j);
        New(j+n,i);
    }
    scanf("%d",&B);
    fo(i,2,B)
    {
        scanf("%d",&j);
        New(j+n+A,i+n+A);
    }
    fo(i,1,n)
    {
        scanf("%d",&j);
        New(j+n+A,i);
    }
    
    d[0][n+1]=d[1][n+A+1]=1;
    dfs(0,n+1);
    dfs(1,n+A+1);
    
    memset(f,127,sizeof(f));
    f[0][0]=0;
    
    fo(i,0,n-1)
    {
        fo(j,0,n-1)
        {
            k=max(i,j)+1;
            
            l=lca(0,i,k);
            f[k][j]=min(f[k][j],f[i][j]+(d[0][k]-d[0][l]-1));
            
            l=lca(1,j,k);
            f[i][k]=min(f[i][k],f[i][j]+(d[1][k]-d[1][l]-1));
        }
    }
    
    ans=2133333333;
    fo(i,0,n-1)
    ans=min(ans,min(f[i][n],f[n][i]));
    
    printf("%d\n",(A-1)+(B-1)-ans);
}