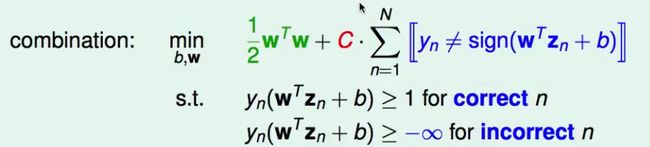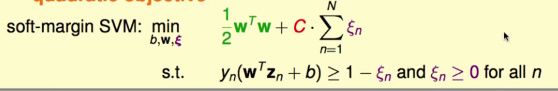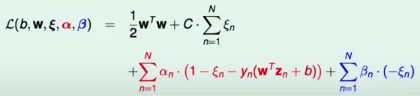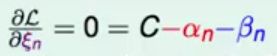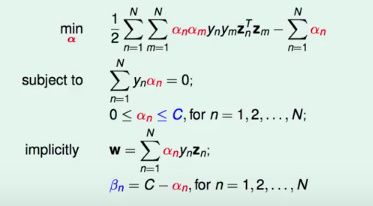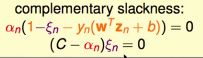本文参考整理了Coursera上由NTU的林轩田讲授的《机器学习技法》课程的第四章的内容,主要介绍了Soft-Margin SVM和它的对偶问题的基本推导过程,主要介绍了Soft-Margin引入的动机、dual problem、αn的物理意义(包括bounded SV、free SV、non SV)及SVM中模型和参数如何选择等内容,文中的图片都是截取自在线课程的讲义。
欢迎到我的博客跟踪最新的内容变化。
如果有任何错误或者建议,欢迎指出,感激不尽!
--
本系列文章已发四章,前三章的地址如下:
- 一、线性SVM
- 二、SVM的对偶问题
- 三、Kernel SVM
引入Soft Margin的动机
利用上一章所讲的Kernel,我们可以利用很多复杂的模型,比如Gaussian Kernel允许我们进行无限多维度的特征转换,虽然有Large Margin的控制来减少VC维度,但还是可能Overfitting。产生过拟合的原因,一方面是因为我们的模型实在太powerful,另一方面与我们坚持要求分隔界限必须完美划分OO和XX的Hard Margin要求也密不可分,如果我们能够放松要求,允许一些点被划分错误,也可能会少fit一些Noise,减少一些Overfitting的可能。
Give Up On Some Examples
在《机器学习基石》中,我们学到的第一个模型是Pocket,它的思想是当没有办法完美分开OO和XX时,我们找一条犯错误最少的线就好。
再看Hard-Margin SVM的要求,它的要求更加苛刻,除了要全划分对,还要选W最短的,即
类似的,我们将两者相结合
系数C用来衡量Large-Margin和犯错误之间的相对重要性。
该问题就是我们的新问题,即Soft-Margin SVM。
化简Soft Margin SVM
将正确分类的点的要求和错误分类的点的要求写成一个式子,如下
注意这里有个问题,这里的运算包含一个[[]]布尔操作,它不是线性约束,所以问题也不再是QP问题,也不再能用之前所推导的对偶问题、Kernel Trick等技法。
而且,这里也没办法区分错误的大小,到底错误点的偏离程度有多大。
下面用一个新式子来表达这种带有错误衡量的Soft Margin SVM问题,而且该问题还是一个QP的形式。
我们用ξn来代表(Xn,yn)离正确分类的yn一侧的胖胖的边界线的错误偏离程度。即如果是正确的点,应该满足yn(W’Zn+b)>=1,且左侧的值越大,则点离线W’Zn+b=0越远,最近的点,即margin上的点,满足yn(W’Zn+b)=1;而错误的进入了软性的margin内,甚至到达反向的对侧的点,yn(W’Zn+b)肯定都严格小于1,且越小偏离越远,我们用一个ξn来衡量这种偏离度,即使得yn(W’Zn+b)>=1-ξn一直成立,同时要求ξn>=0尽可能小,这样对于正确的点,本来就大于1,ξn自然为0;而错误的点则需要1-正数ξ来纠正偏离,ξn就衡量了点犯错误的大小程度。我们之前的式子,用犯错的点的总个数来衡量错误,现在的式子用每个点的犯错程度的总和来衡量,而且形式也是一个二次规划QP的形式,新的式子如下:
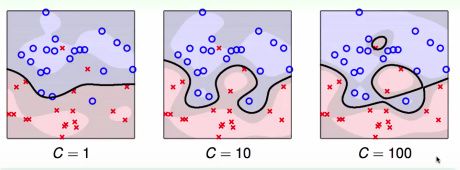
参数C:large margin和margin violation的trade-off
- C很大:margin-violation的惩罚很大,尽可能少犯错误
- C很小:margin大一点,很多点犯错没什么大关系,因为惩罚很小
该QP问题有d+1+N个变量,其中d+1是之前的W和b,增加的N个是记录每个点的犯错程度的ξn;有2N个约束,增加的N个约束是ξn>=0。
下一步,我们将仿照之前推导Dual SVM的方法,重新推导Soft Margin SVM的对偶问题,并尝试利用kernel trick移除对d~的依赖。
Soft Margin SVM的对偶问题
原始问题:
原来变量的约束还是用αn来代表其lagrange multipliers,我们用βn来代表新增加的变量约束ξn>=0的lagrange multipliers,得到Lagrange Function如下:
其对应的Lagrange Dual问题如下:
代入Lagrange Function,如下
对变量ξn偏微分,
所以,我们可以把βn换成C-αn,再满足条件βn>=0,则有αn<=C,加上原来的条件αn>=0,则得到0<=αn<=C,这样就完全不用考虑β了。
用C-αn消去β后,化简后如下
发现,所有的ξn也被消掉了,就像之前在Hard-Margin SVM Dual的问题中,把b消去一样。
式子变简单了,如下
发现这个式子和之前Hard Margin SVM的Lagrange Dual基本一样,只是多了αn<=C的条件,接下来按照之前的步骤化简,对b微分,消去b,对W微分,用αn对ynZn的线性表示替换W,变成只有一个变量α的最优化问题,比较简单,请参考前面推导Hard Margin SVM Dual的过程。
最终会得到Soft Margin SVM Dual的标准形式。
Standard Soft-Margin SVM Dual
唯一的差别就是增加了条件αn<=C和隐式的βn=C-αn的条件。
这是另外一个QP问题,有N个变量,2N+1个条件,它也是个convex的问题。
Kernel Soft-Margin SVM
基本过程
基本和Hard-Margin一样,但是比Hard-Margin更加灵活,因为可以控制参数C。
而且Soft-Margin不论是Primal还是Dual总是有解,而不像Hard-Margin的问题需要数据linear-separable,因此在实践中Soft-Margin经常使用。
如何算b?
对于Hard-Margin SVM,我们利用互补松弛条件和一个SV就可以算出b
对于Soft-Margin SVM,也有类似的complementary slackness条件
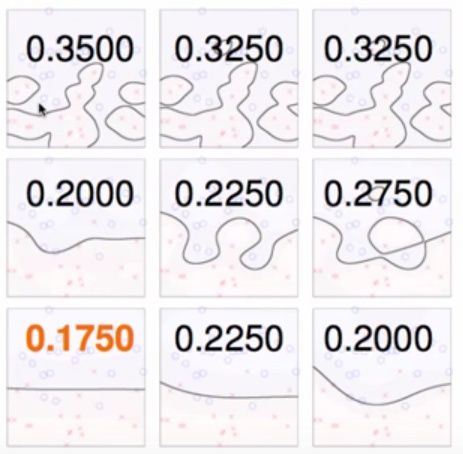
所以,要解出唯一的b,需要找一个自由支撑向量(Xs,ys),即0<αs 如果没有free SV(极少数的情况下),则b只能被一堆不等式所表示,只要不等式范围内的b满足所有的KKT条件,则这些b都是可以的。 灰色的部分代表margin内部,越大的C,对错误的惩罚就越大,就尽可能少犯错,就越可能fit Noise,对Noise的容忍度就越小,就越可能Overfit。 注意:如果参数调节不好,就算是Soft-Margin SVM还是有可能产生Overfit的! 因此,对于Soft-Margin Gaussian SVM,我们需要仔细地选择参数(γ,C)。 哈利波特条件(Complementary Slackness): 之所以叫哈利波特条件,是因为左边的两个括号,如果一个不为0,另一个一定为0,就像哈利波特和伏地魔两者至少必有一个死亡。 可以把点分成3类: 注意:violation有两种,一种是小小的违反,只是进入margin而没有跨过中线,虽然有小小的违反,但是没有造成我们的分类错误;还有一种是大大的违反,已经跨过中线,造成分类错误。 因此,利用αn可以帮助我们进行数据的分析。 bounded SV是唯一可能造成Ein错误的点,如果ξn>=1,意味着这种violation造成了0/1分类错误,如果0<=ξn<1,就不会造成0/1分类错误。因此,Ein的可能范围在0.0000<=Ein(gsvm)<=#(bounded SVs)/N 上图9个全部都是Soft-Margin Gaussian SVM,横轴是使用了不同的参数C,纵轴是使用了不同的参数γ。 如何选择哪组参数对应的模型最好呢? 之前《机器学习基石》课程告诉我们最简单好用的工具就是Validation。 利用Cross Validation的值选择 我们能不能做最优化? 不能。因为对于每个(C,γ),Ecv(C,γ)不是(C,γ)的平滑函数,很难最优化,通常只能送进去几个不同的(C,γ)值,看看哪一个最好。 我么可以用V-fold cross Validation在几个不同的(C,γ)上选择最合适的model。 对于SVM来说,Cross Validation是一个非常常用的方式来选择适当的参数。 V-fold的极限:E(loocv) = E(cv) with N folds LOO在SVM有一个有趣的结果: 证明:对于点(Xn,yn),如果刚好最优αn=0,即说明该点不是SV,则对于去掉点(Xn,yn)后的数据集,(α1,α2,α3....αn-1,αn+1,...,αN)这一组α仍然是去掉点后的数据集的最优解,假设不是最优解,存在更好的解,把αn=0加回去,则构造了最开始数据集的一个更优解,矛盾。 则对SVM来说,g-=g(当去掉一个non-SV点后) 而e(SV) <= 1 则不难得到以上bound,即E(loocv) <= #SV/N 所以,我们可以近似用这个做模型的选择 利用#SV做模型的选择 数字是SV的数量。 注意:#SV只是一个上限,并不代表真正的loocv。 常用#SV来排除一些危险的模型,再做cross validation选择一个最适合的参数。即#SV常用来做安全检查(safety-check),如果计算Ecv太过于耗时。 我们从最开始的Linear Hard-Margin SVM开始推导,研究了它的Dual Problem,并利用Kernel Trick简化了transform + inner product的运算,这一讲又讨论了在实践中最常用的Soft-Margin SVM的问题,但这些都是在做最基本的binary classification,下一讲我们将把学过的SVM模型应用到更多的问题上,比如soft binary classification,即logistic regression问题,敬请关注。实际的Soft-Margin Gaussian SVM
αn的物理含义
实践需要:模型选择
V折交叉验证
Leave-One-Out CV
Mind Map Summary
如果您对这一系列文章感兴趣,欢迎订阅我的专题或者关注我以获得最新的更新信息!
本文首发于我的博客,如果您想提前看到更多的内容或者懒于寻找之前的章节,可以直接来我的博客阅读长文版,感谢您的鼓励支持!