这篇文章收录在我的 Github 上 algorithms-tutorial,另外记录了些算法题解,感兴趣的可以看看,转载请注明出处。
(一) 基本概念
Red-Black Tree 称为“红黑树”,是一种自平衡二叉查找树,红黑树和 AVL 树类似,在进行插入和删除时需要通过旋转和重新着色来维持其红黑树的特性。
红黑树的应用相当广泛,主要是用它来存储有序的数据,它的时间复杂度为 O(logn),查询效率非常高。
1. 红黑树和 AVL 树的区别:
- 红黑树并不追求“完全平衡” —— 它只要求部分地达到平衡要求,降低了对旋转的要求,从而提高了性能。
- 在AVL树中任何节点的两个儿子子树的高度最大差别为一,所以它也被称为高度平衡树。
- 红黑树的算法时间复杂度和 AVL 相同,但统计性能比 AVL 树更高。
- 红黑树是牺牲了严格的高度平衡的优越条件为代价红黑树能够以 O(log2 n) 的时间复杂度进行搜索、插入、删除操作。由于它的设计,任何不平衡都会在三次旋转之内解决。
2. 红黑树的执行:
- 每个节点具有颜色属性,要么为红色,要么为黑色
- 根节点是黑色的
- 每个叶子节点 (null) 是黑色的 (这里叶子节点,指为空的叶子节点)
- 如果一个节点是红色的,则其子节点必须是黑色的
- 从一个节点到该节点的叶节点 (null) 所有路径包含相同数目的黑节点
3. 红黑树的优点:
- 红黑树的性质决定了从根节点到最远的叶节点的距离不可能超过从根节点到叶节点的距离的两倍。
- 另外可以证明的是红黑树的高度最多为 log(n + 1),n 为节点个数
- 插入和删除在最坏的情况下为 O(logn)
- 红黑树提供了一种替代 AVL 树的方式,并且是一种更加简单,不用递归的插入算法
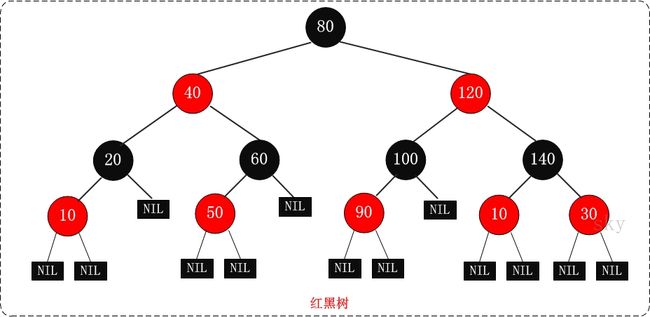
4. 红黑树的示意图:
(二) 基本操作
红黑树的基本操作是添加、删除。前面我们提到,在进行插入和删除时需要通过旋转和重新着色来维持其红黑树的特性,那么接下来就介绍这些操作:
一、左旋和右旋:
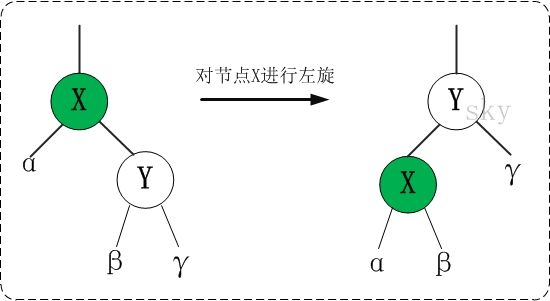
1. 左旋:
可以将 X 称为当前节点,则左旋的字面意思就是将当前节点变为左子节点。(这样可避免左右旋傻傻分不清)
这时候 X 变为 Y 的左子节点,若 Y 节点存在左子树(即图中的 β),则将其变为 X 的右子树
Java 代码实现:
public TreeNode singleRotateWithLeft(TreeNode presentNode){
TreeNode node; //新的父节点
node = presentNode.rightChild;
presentNode.rightChild = node.leftChild;
node.leftChild = presentNode;
return node;
}
2. 右旋:
此时当前节点为 Y,则 Y节点变为 X 节点的右子树,而若 X 存在右子树(即图中的 β),则变为 Y 节点的左子树
Java 代码实现:
public TreeNode singleRotateWithRight(TreeNode presentNode){
TreeNode node;
node = presentNode.leftChild;
presentNode.leftChild = node.rightChild;
node.rightChild = presentNode;
return node;
}
二、插入:
一个节点要插入到红黑树中,需要的步骤:
- 将红黑树当作一棵二叉查找树,将节点插入
- 将该节点着色为红色
- 通过旋转和重新着色等方法修正该树,使之重新成为一棵红黑树
第一步:将红黑树当作一棵二叉查找树,将节点插入
红黑树本身也是二叉查找树,将节点插入后,该树仍是二叉查找树。
第二步:将该节点着色为红色
将插入的节点着色为红色,不会违背特性(5):从一个节点到该节点的叶节点 (null) 所有路径包含相同数目的黑节点
若插入的节点为黑色,那么该路径的节点就多了一个黑节点,这显然与特性(5) 相违背。
第三步:通过旋转和重新着色等方法修正该树,使之重新成为一棵红黑树
第二步中,将插入的节点着色为 "红色" 之后,不会违背特性 (5),那么它还会违背其他特性吗?
对于特性(1) (2) (3) 显然都不会违背,请自行想象
而对于特性 (4),是有可能违背的
因为插入节点的父节点也可能为红色,那么显然与一个红色节点的子节点必须为黑节点相违背。
那么,既然有可能违背特性(4) 那么我们可以通过旋转或者重新着色来使其满足特性(4),再次成为红黑树。
无论旋转还是重新着色,其核心思路都是:将红色的节点移到根节点;然后,将根节点设为黑色。
对于插入节点的情况,可以大致分为以下五种:
情况1:被插入的节点是根节点
处理方式:直接把此节点涂为黑色。
这个显然,不然就会违背特性(2): 根节点是黑色的
代码实现:
public void insert_case1(TreeNode presentNode){
if(presentNode.parent == null){
presentNode.color = "black";
}else{
insert_case2(presentNode);
}
}
情况2: 被插入的节点的父节点是黑色
处理方式:什么都不需要做,节点被插入后,仍然是红黑树。
代码实现:
public void insert_case2(TreeNode presentNode){
if(presentNode.parent.color.equals("black")){
// do nothing
}else{
insert_case3(presentNode);
}
}
情况3、4、5 就比较复杂了些,但是核心思路仍是:将红色的节点移到根节点;然后,将根节点设为黑色。
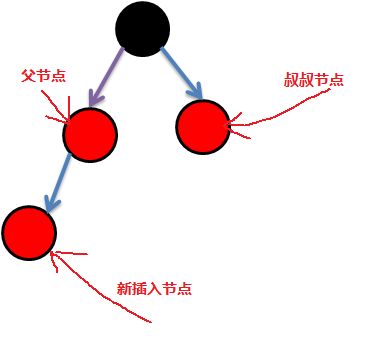
在介绍方法之前,先来了解几个概念:
如图所示,新插入节点的父节点的父节点(即图中黑节点)即是新插入节点的祖父节点,而祖父节点的右子节点称为叔叔节点。
以后代码部分的基础数据结构 ADT 都是用这个节点树来实现的:
//java
public class TreeNode{
TreeNode leftChild;
TreeNode rightChild;
TreeNode parent;
TreeNode grandParent;
TreeNode uncle;
String color;
public TreeNode(){
grandParent = this.parent.parent;
if(this.parent == grandParent.leftChild){
uncle = grandParent.rightChild;
}else{
uncle = grandParent.leftChild;
}
}
}
情况3、4、5 都是建立在插入节点的父节点为红色的情况下,此时会违背特性(4),所以我们需要通过旋转和重新着色来修复红黑树
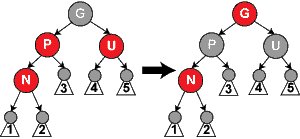
情况3: 叔叔节点是红色
处理方式:
- 将 "父节点" 设为黑色
- 将 "叔叔节点" 设为黑色
- 将 "祖父节点" 设为红色
- 将 "祖父节点" 设为 "当前节点"(红色节点);之后继续对 "当前" 进行操作
新插入节点为 N,符合情况 3 要求,则将 P,U 变为黑色,G 变为红色,之后再将 G 作为当前节点继续判断,因为 G 为根节点,那么根据情况 1,将其涂为黑色,完事。
代码实现:
public void insert_case3(TreeNode presentNode){
if(presentNode.uncle != null && presentNode.uncle.color.equals("red")){
presentNode.parent.color = "black";
presentNode.uncle.color = "black";
grandParent.color = "red";
insert_case1(grandParent);
}else{
insert_case4(presentNode);
}
}
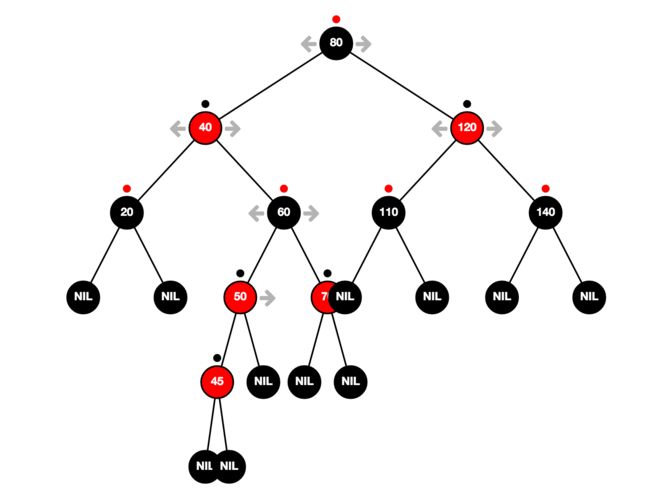
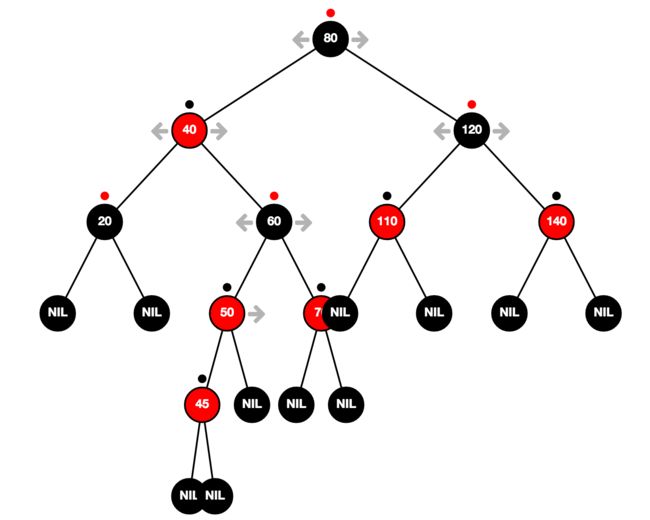
我再举个例子来说明:往一课红黑树中插入节点 45
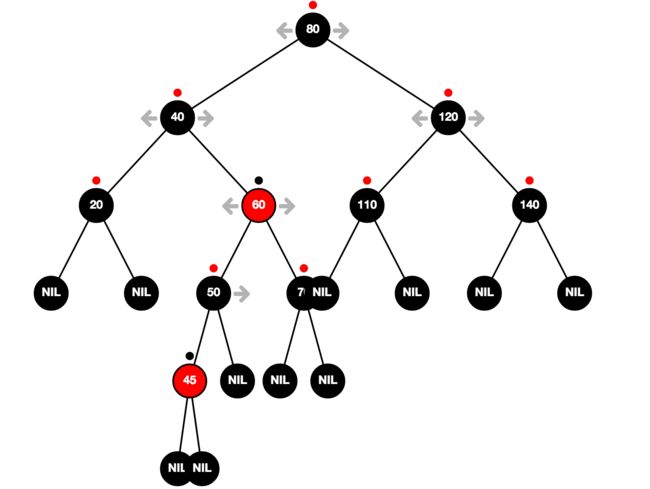
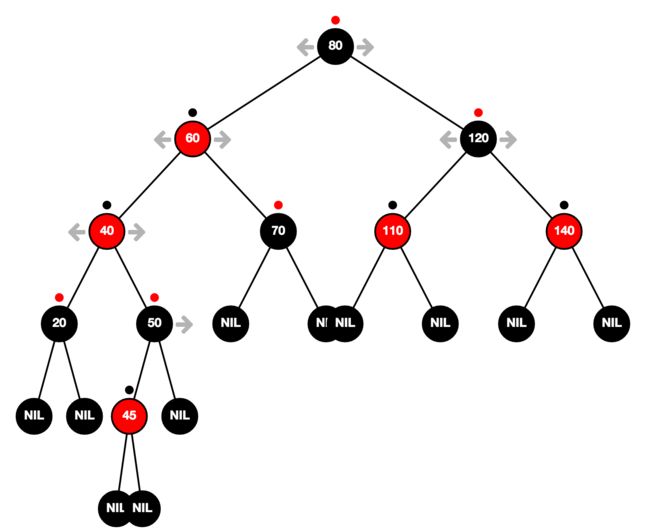
符合情况 3,所以颜色重绘并将节点 60 作为当前节点,就变为了
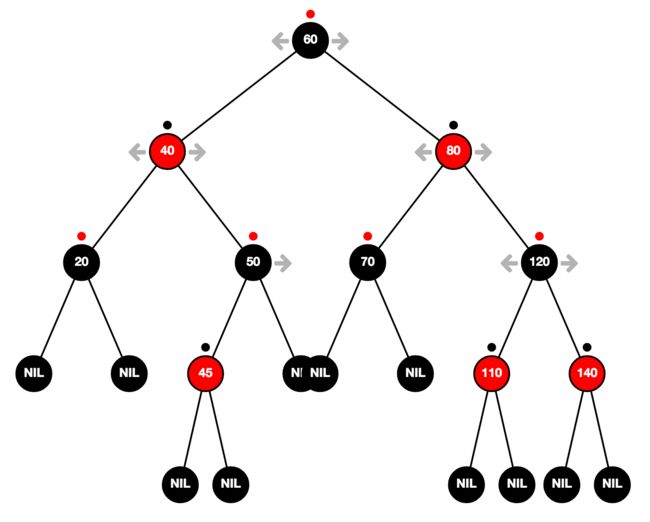
之后又符合情况 3,所以继续操作,最后将根节点涂成黑色就结束了
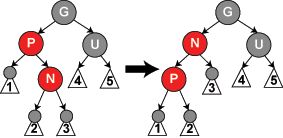
情况 4:叔叔节点为黑色或缺失,且当前节点是曲线边 (即左右或右左)
处理方式:
- 将 "父节点" 作为 "新的当前节点"
- 以 "新的当前节点" 为支点进行左旋
- 以新的当前节点(即原本的父节点)再进行操作
如图所示:
将 P 节点作为当前节点进行左旋,然后之后再对 P 节点进行操作
代码实现:
public void insert_case4(TreeNode presentNode){
if(presentNode == presentNode.parent.rightChild && presentNode.parent == presentNode.grandParent.leftChild){
singleRotateWithLeft(presentNode.parent);
presentNode = presentNode.leftChild;
}else if(presentNode == presentNode.parent.leftChild && presentNode.parent == presentNode.grandParent.rightChild){
singleRotateWithRight(presentNode.parent);
presentNode = presentNode.rightChild;
}
insert_case5(presentNode);
}
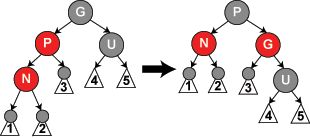
情况 5: 叔叔节点为黑色或缺失,且当前节点是在外边(即左左或右右)
处理方式:
- 将 "父节点" 设为黑色
- 将 "祖父节点" 设为红色
- 以 "祖父节点" 为支点进行右旋
如图所示:
代码实现:
public void insert_case5(TreeNode presentNode){
presentNode.parent.color = "black";
presentNode.grandParent.color = "red";
if(presentNode == presentNode.parent.leftChild && presentNode.parent == presentNode.grandParent.leftChild){
singleRotateWithRight(presentNode);
}else{
singleRotateWithLeft(presentNode);
}
}
让我们用一个例子来结合说明情况 3、4、5
往图中原本的红黑树插入节点 45,这里先用到情况3,接着 4,最后 5,所以不再赘述原理。
step1:
step2
step3
前面代码部分都是用尾递归来实现插入操作,显然这种插入效率并不高,截下来我改用迭代的方式来进行插入操作
迭代实现插入操作
public void insert_case(TreeNode presentNode){
while(presentNode != null){
if(presentNode.parent == null){
presentNode.color = "black";
break;
}else if(presentNode.parent.color.equals("black")){
//do nothing
break;
}else if(presentNode.uncle != null && presentNode.uncle.color.equals("red")){
presentNode.parent.color = "black";
presentNode.uncle.color = "black";
presentNode.grandParent.color = "red";
presentNode = presentNode.grandParent;
}else if(presentNode == presentNode.parent.rightChild && presentNode.parent == presentNode.grandParent.leftChild){
singleRotateWithLeft(presentNode.parent);
presentNode = presentNode.leftChild;
}else if(presentNode == presentNode.parent.leftChild && presentNode.parent == presentNode.grandParent.rightChild){
singleRotateWithRight(presentNode.parent);
presentNode = presentNode.rightChild;
}else{
presentNode.parent.color = "black";
presentNode.grandParent.color = "red";
if(presentNode == presentNode.parent.leftChild && presentNode.parent == presentNode.grandParent.leftChild){
singleRotateWithRight(presentNode);
}else{
singleRotateWithLeft(presentNode);
}
}
}
}
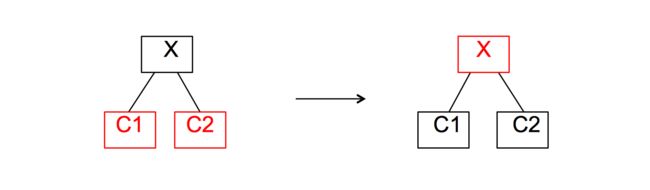
另外老师还介绍了一种 Top-down 的插入方法:从根节点到插入的节点的路径中查找,如果遇到一个节点 X 带有两个红色儿子,就执行下面的操作:
这样就会遇到一个问题:如果节点 X 的父节点也是红色,那就违背了性质 4,这时候我们就要根据前一种方法的情况 3、4、5去进行讨论
课上例题:构造一棵红黑树,按顺序加入 10,85,15,70,20,60,30,50,65,80,90,40,5,55
三、删除:
将红黑树内的某一个节点删除。需要执行的操作依次是:
- 将红黑树当作一颗二叉查找树,将该节点从二叉查找树中删除
- 通过"旋转和重新着色"等一系列来修正该树,使之重新成为一棵红黑树
在分析之前,我们再次温习一下红黑树的几个特性:
- 每个节点具有颜色属性,要么为红色,要么为黑色
- 根节点是黑色的
- 每个叶子节点 (null) 是黑色的 (这里叶子节点,指为空的叶子节点)
- 如果一个节点是红色的,则其子节点必须是黑色的
- 从一个节点到该节点的叶节点 (null) 所有路径包含相同数目的黑节点
参考链接:
- 红黑树 - 维基百科,自由的百科全书
- 红黑树(一)之 原理和算法详细介绍 - 如果天空不死 - 博客园