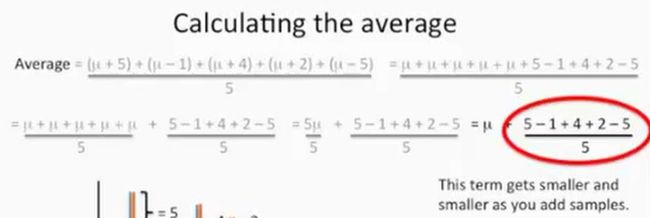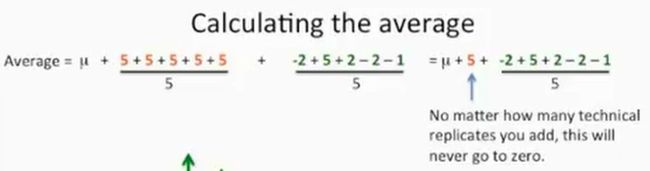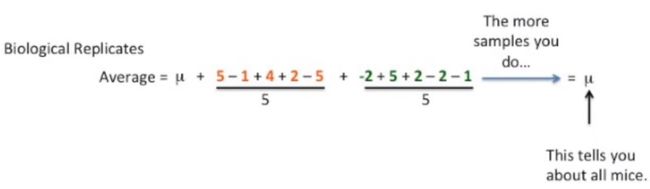前言
这是StatQuest系列视频教程笔记的最后一篇,我在YouTube上看了一下,作者还有其他的几个视频,有兴趣的同学还可以看看。这篇笔记是视频教程的第62节,主要内容是讲RNA-Seq中的技术重复问题。
是否需要技术重复
前面有一篇笔记我们提到了技术重复与生物重复。但在RNA-Seq中,我们是否需要做技术重复呢?
答案是否,如果你做了生物学重复,就不需要做技术重复。或许有同学知道这个答案,但是却不清楚为什么做了生物学重复后,就不需要做技术重复了呢,后面我们就会回答这个问题,如下所示:
RNA-Seq变异的两个来源
RNA-Seq的测序数据的变异(variation)主要来源两个方面,第一个是生物学变异(Biological Variation),第二个是技术变异(technical variation)。
生物学变异
生物学变异是指生物本身本身造成的变异,例如,即使是遗传背景完全一样的小鼠,例如像C57BL/6N这样遗传背景都非常清楚的小鼠,也不存在RNA转录本数目完全相同的两只小鼠(只能是接近,而不是完全相同)。
任何物种的两个生物个体都不可能完全一样,无论这种生物是人,小鼠,还是果蝇。
技术变异
每当我们做一个实验时,在实验过程中都会参杂一些零碎的非实验因素(例如今天你的心情,不同批次的培养基,移液枪的吹打次数,细胞培养的时间,细胞的传代次数等等),其中的一些是完全100%的随机因素。因此,当我们再次重复这个实验的时,即使实验条件与上一次的实验条件完全相同,也不可能得到与上次实验100%相同的结果(当然,总体的结果会相差不大,会很接近),如下所示:
生物学变异的案例
为了说明这生物学变异和技术变异的问题,我们先来看一个简单的案例。
在这个案例中,我们只研究生物学变异。例如,我们对几只小鼠做了RNA-Seq,没有做任何技术重复。在下面的二维坐标系中,X轴是小鼠的编号,Y轴是小鼠基因X的reads数,下图是第1只小鼠的数据,如下所示:
我们再看一下第2只小鼠的数据,如下所示:
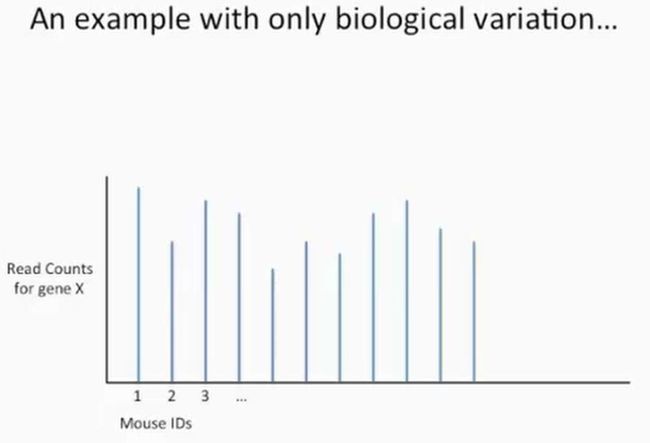
由于我们没有做技术重复,因此从上图中,我们可以知道,第2只小鼠与第1只小鼠的基因X的reads数差异就是完全来源于生物学变异了,也就是这两只小鼠自身的变异,现在看第其它小鼠的数据,如下所示:
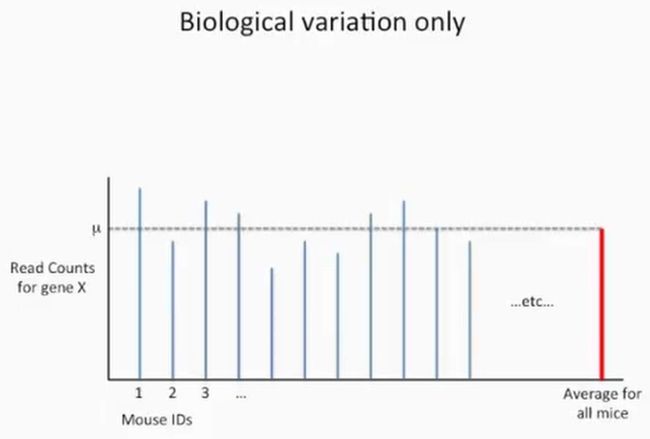
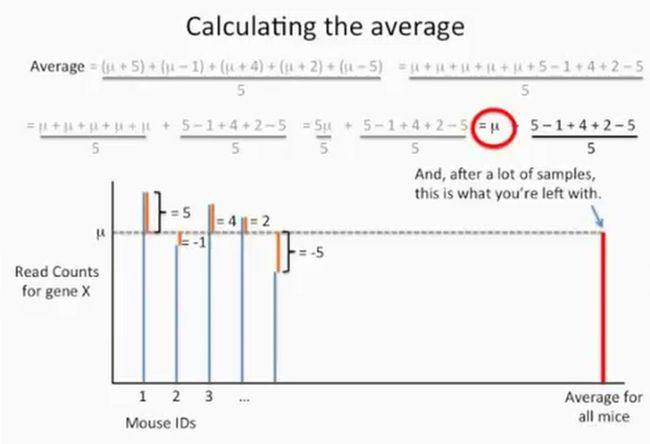
假设我们把地球上的所有小鼠都给测了,也就是说上图的X轴上有无数个小鼠的基因X的reads数,此时,我们求出这所有小鼠基因X的reads数的平均值,并用希腊字母μ表示,这个μ就是小鼠基因X的reads数真正的均值,就是下面的这个样子:
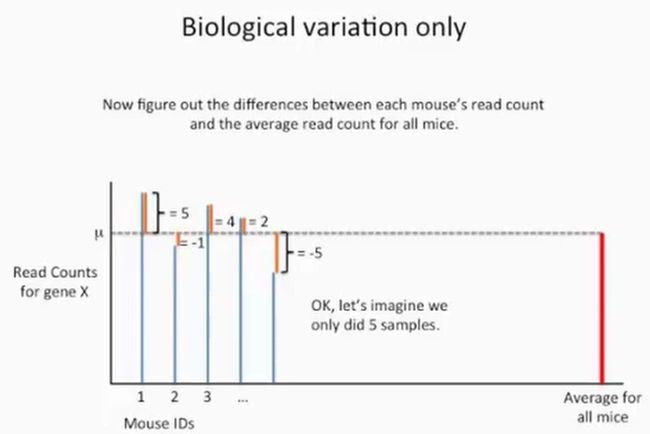
现在我们计算出每只小鼠基因X的reads数与真实均值μ的差值,先看第1只小鼠,它与均值μ的差值是5,如下所示:
现在再计算出剩下的所有小鼠的基因X的reads数与reads数平均值的差值,为了方便说明问题,这里我们只计算前5只小鼠的数据,如下所示:
此时,我们使用数学公式来表示这前5只小鼠的基因X的reads数,这个公式很简单,如下所示:
现在我们计算出这5只小鼠的基因X的reads数的均值,如下所示:
把上面的公式再整理一下,应时下面的这个样子,如下所示:
其中上图公式右侧红圏的部分是几个常数,也就是每只小鼠基因X的reads数与均值μ的差值的均值,并且这个红圏中的计算结果(5-1+4+2-5=1)会随着小鼠样本数目的增多而缩小,从而最终近于0,那么上面的均值最终会等于实际的均值μ了,如下所示:
考虑生物学变异与技术变异的情况
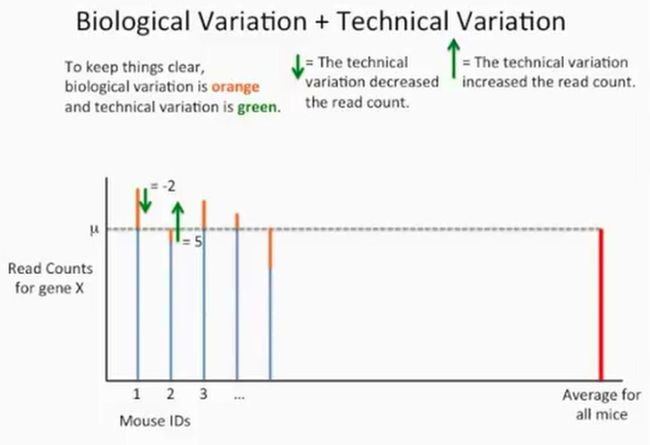
还以上述的案例来说明一下生物学变异和技术变异,为了清楚地说明这两个变异,在下图中,我们使用橘黄色的线段来表示生物学变异,如下所示:
我们使用绿色的箭头来表示技术变异,其中绿色箭头向下表示技术重复导致的reads数降低,绿色箭头向上表示reads数上升的情况,如下所示:
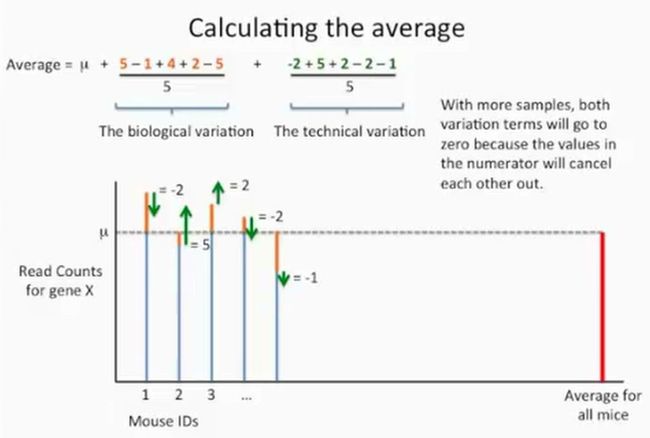
现在我们考虑生物学变异和技术变异的情况下,来计算一下前5只小鼠的基因X的reads数均值,如下所示:
现在整理一下上面的均值公式,我们可以发现,这个公式可以公为3部分,第1部分是均值μ,第2部分是生物学变异,第3部分是技术变异,如果我们增加样本的话,那么这两个变异就会接近于0,因为它们的分子中既有正值,又有负值,因此最终会相互抵消,因此,做了生物学重复(一共有5只小鼠)的这批小鼠的最终基因X的reads均值就是μ,如下所示:
只做技术重复的情况
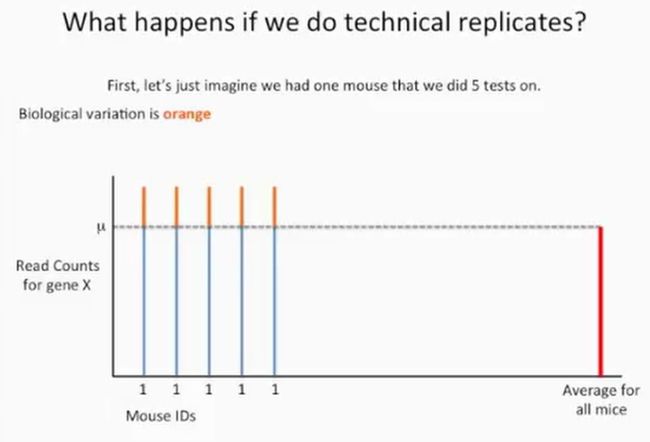
我们现在考虑另外一种情况,即我们只做了技术重复。例如针对第1只小鼠,我们做了5次技术重复,它的基因X的reads数如下所示:
其中生物学变异使用橘黄色表示,橘黄色线段的大小都一样,这是因为对同一只小鼠做了5次技术重复,同一只小鼠的生物学变异是一样的,另外,在下图中我们再添加上技术变异,技术变异使用绿色表示,如下所示:
现在我们计算一下第1只小鼠的基因X的reads数均值,如下所示:
其中我们可以发现,在这个案例中,第1只小鼠的基因X的reads数的均值由3部分构成。
第1部分是实际均值μ,第2部分是生物学变异,它是一个固定的值,因为对于一只确定的小鼠来说,它的生物学变异是确定的,因此针对这只确定的小鼠来说,无论做多少次技术重复,它的生物学变异都是一个固定值,不会相互抵消,在这里,这个值是5。第3部分是技术变异,不过由于技术变异的分子部分有正数,有负数,因此随着技术重复的增多,技术变异的分子会相互抵消,最终接近于0,因此第1只小鼠基因X的reads数的均值最终结果是μ+5。
比较生物学重复和技术重复
生物学重复
现在我们比较一下生物学重复和技术重复,回到我们前面的部分,我们知道,基因X的reads数的平均值公式是由3三部分构成的,其中第1部分是真实的均值μ,第2部分是生物学重复,用橘黄色表示,第3部分是技术重复,用绿色表示,如下所示:
第1部分是真实的均值μ,这里再强调一下,真实的均值可以理解为所有小鼠基因X的reads数的均值,而我们平时所测的小鼠基因X的reads数是对这个均值μ的估计值,因为我们不可能把所有的小鼠基因X都给测了,估计值只能无限接近于真实均值μ,但法等于均值,不过当样本量足够大时,此时的估计值就可以视为均值μ。
公式的第2部分是生物学变异,第3部分是技术变异。由于生物学变异和技术变异的分子部分都是有正值,负值,因此第2部分与第3部分最终会抵消,得到的结果就会非常接近于真正的均值μ,它就代表了所有的小鼠基因X的reads数,如下所示:
无生物学重复
现在我们再看一下无生物学重复,有技术重复的情况下,我们计算一下第1只小鼠的基因X的reads数均值,如下所示:
这个公式由3部分组成,即真实均值μ,生物学变异和-技术变异,如果我们不断地增加样本,那么这个均值就成了Average = μ +5,最终这个结果只能提供第1只小鼠的信息,而非其它所有小鼠的信息,也就是说,此时的这个μ+5只是第1只小鼠基因X的reads数均值,而不是真实的均值μ,它不能代表整个小鼠的基因X的reads数,如下所示:
结论就是,如果我们只对这个小鼠做多次技术重复,最终得到的数据就是这个小鼠的数据,不具有代表性,也就是说,如果别人的实验室重复这个实验的话,有可能重复不出来。
同时做生物学重复和技术重复
此时我们可能会想,如果我既做了生物学重复,又做了技术重复,那么是不是能得到最精确的结果?
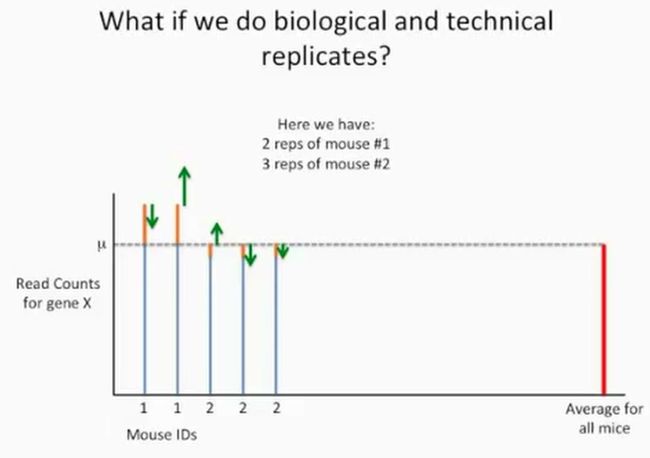
很不幸,答案是否定的。在下面的这个案例中,我们对第1只小鼠做了2个技术重复,第2只小鼠做了3个技术重复,如下所示:
那么我们求出均值,如下所示:
如果我们不再做另外的生物学重复,那么上述公式的第2部分(也就是橘黄色的生物学变异部分)就不会相互抵消,最终接近于0,如下所示:
但是,如果做了更多的生物学重复,那么它会接近于0,不过需要的生物学重复数量会更多,因为如果生物学重复的数量量不是特别多的话,这第2部分就不会很快地接近0,如下所示:
我们就看一下,将中间这一项相互抵消为0需要多少个生物学重复。我们对第2只小鼠做了3次技术重复,这3次技术重复中,每个技术重复的生物学变异是相同的,例如第2只小鼠的生物学变异是-1,那么第2只小鼠做了3次技术重复,这3次技术重复的变异分别为2,-2,-1(图中数据),由于是同一只小鼠,那么这3次技术变异对应的生物学变异是一样的,分别是-1,-1,-1(还是图中数据)。
因此,为了降低这种生物学变异的程度,至少也是降低到与前面测了5只小鼠(第1只小鼠到第5只小鼠)同等的水平,那么我们一共需要做15次,这15次就是:5个生物学重复,1个生物学重复做3次技术重复,一共是15次。用公式表示就是下图中的最后一行,如下所示:
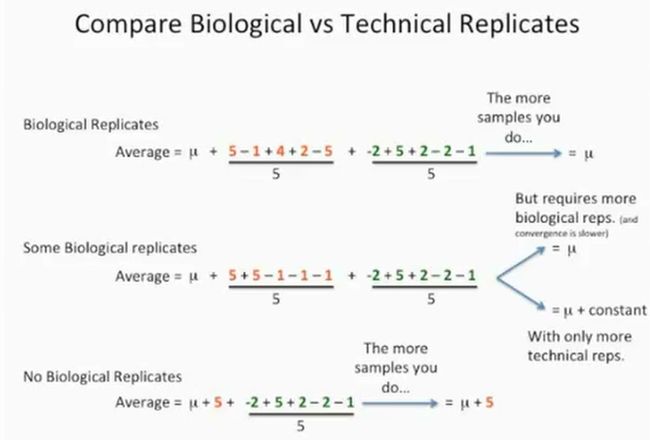
现在我们比较一下这三种实验(分别是①只做生物学重复;②既做生物学重复,又做技术重复;③只做技术重复)的情况:
从上述的结果我们可以发现这些规律:
- 只做生物学生重复的结果最接近于均值μ,这是最好的结果;
- 既做了生物学重复,又做了技术重复的话,它要么接近于均值μ(这个需要做更多的生物学重复,生物学重复与技术重复加起来要做15次),要么是均值
μ+常数(只做更多的技术重复,不做更多的生物学重复); - 最差的结果就是不做生物学重复,只做技术重复,如下所示:
结论就是,只做生物学重复就行了,就像上面的第1种情况,此时,我们只需要测序5次即可,如果既做生物学重复,又做技术重复,那么我们就需要测序15次,相当于成本直接上升到原来的3倍。