【写在前面】
作为一名终身学习实践者,我持之以恒地学习各种深度学习和机器学习的新知识。一个无聊的假日里我突然想到:反正一样要记笔记,为什么不把我学习的笔记写成博客供大家一起交流呢?于是,我就化身数据女侠,打算用博客分享的方式开启我的深度学习深度学习之旅。
本文仅供学习交流使用,侵权必删,不用于商业目的,转载须注明出处。
【学习心得】
Coursera和deeplearning.ai合作的Deep Learning Specialization出得真是慢啊……现在只出了Course 1:Neural Networks and Deep Learning,之后还有4个courses。虽然在我和大多数深度学习从业人员看来是非常基(jian)础(dan)的,但是有时候习题居然还会做错。鄙人资质平平,看来还是得时不时重温一下这种基础课程。虚心求学切忌自空自大。
【学习笔记】
Andrew第一堂课一共四周,每周的课业量都在增加。可以看到Coursera逐渐增加了练习题的比例,这一进步我个人很喜欢,建议大家也都去做一下课后的练习题,特别Python部分的。
前三周每周最后有个对deep learning heroes的采访,除了第一周的Geoffrey Hinton我看了之外,后面的Pieter Abbeel和Ian Goodfellow我都没看,时间太长了。主要是因为教材对于学员过于基础的话,学习时本身就容易走神,所以我就不想再花费有限的注意力了,以后有兴趣还会回来看一下的。
我按照理论知识+Python实践两大模块来总结一下。注意这里只是我个人对课程的总结,侧重于我薄弱的环节,建议感兴趣的读者还是去Coursera上购买教材,这样学习得才更全面。经费紧张的读者也不用担心,前7天是免费的。
Deep Neural Networks
什么是神经网络?
神经网络 (Neural Network) 并不是一个新鲜的名词,但是随着数据、计算力、理论三方面的突破,近些年来才迎来了寒冬后的春天。神经网络主要是由神经元 (neuron) 构成的,一个neuron通常是多个输入的线性组合+一个激活函数,其中激活函数往往是非线性函数。像人类的大脑一样,许多个神经元由多种链接组合起来之后,就具有了强大的能力。Andrew一开始就给了两个最简单的例子。
1) 单神经元网络 (single neural network)
如果我们的输入里只有一个变量,在它之上应用一个ReLU函数就构成了一个单神经元的网络。ReLU函数全称是Rectified Linear Unit,不要被这个名称吓唬到了,其实深度学习完全是纸老虎,ReLU其实就是一个max函数,有点类似于MARS。它的形状是这样的:
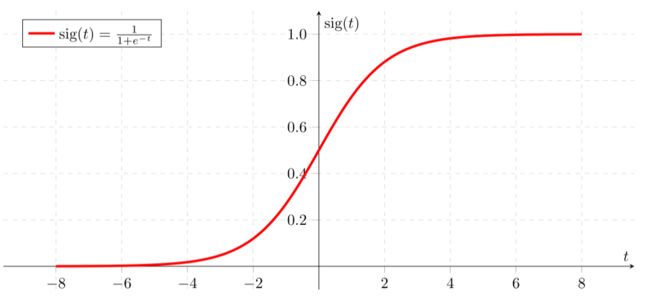
上图是传统的sigmoid函数,不仅常用在logistic regression中,深度学习中也会使用到的。当你比较ReLU函数和sigmoid函数时就会发现:ReLU将一部分的数据舍弃替换为0,这使得计算大规模的数据时比sigmoid更快(试想如果每一层ReLU舍弃了50%的无用数据,那么4层之后数据量就是原来的6%,当然真实的情况没有这么简单),而ReLU另一部分的导数为1,在反向传播时计算梯度很方便;sigmoid函数则处处可导,但是在绝大多数的值域上导数非常小,这使得它没有过滤掉不需要的数据的能力、大幅降低了梯度下降的学习速度,并且在反向传播时可能会有梯度消失的问题。
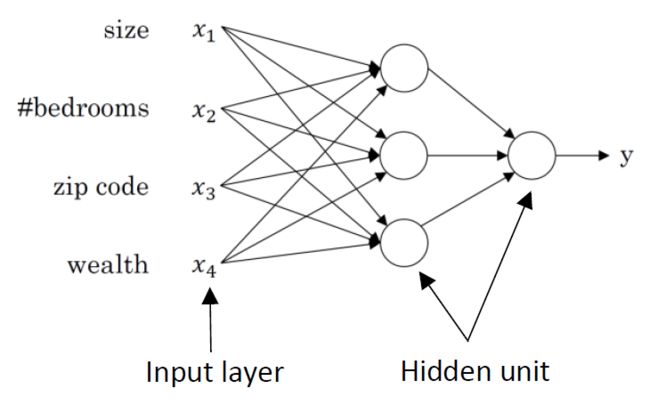
2) 多神经元网络 (multiple neural network)
深度学习不仅可以应用于传统的结构化数据,也应用在声音、图像、文字等非结构化的数据上。前一段时间讲课的时候,提到了深度学习的应用。我想表达深度学习与传统方法相比,更方便处理非结构化的数据。结果居然一时把structured这个词给忘记了,卡了半天最后忽悠了一个二维vs.多维——其实我的本意是structured vs. unstructured。还好那只是一语带过,不是知识点,估计也没人注意到。可见尽信书则不如无书,尤其是在deep learning这样新兴、鱼龙混杂的行业。
以神经网络的结构看逻辑回归 (Logistic Regression)
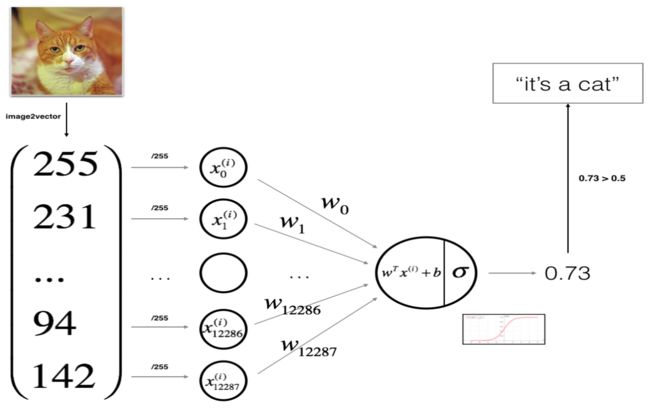
大家所熟悉的逻辑回归可以看做一个最简单的神经网络,其中z是输入特征的线性组合,而sigmoid函数是对z的非线性转换。因此,Andrew以Logistic regression为切入口、以矢量化后的图片为输入,构建了一个最基础的神经网络。图片的输入本来是三维的(二维的像素点再加上RGB三种颜色),通过image2vector将每一张图片转化为一个宽为1的矩阵——一个将(a,b,c,d)维度的张量flatten为(b*c*d, a)的小技巧:X_flatten = X.reshape(X.shape[0], -1).T,其中X.T是X的转置,而a代表的是样本数。
概括来讲,神经网络的建模主要包括以下几个主要步骤:
1. 定义模型结构,比如多少层、什么激活函数、多少输入特征,等等;
2. 初始化模型参数,在logistic regression这个例子中,只需初始化W和b为0就可以了,并且不需要加入一些抖动;
3. 进行num_iterations次循环:
3.1 前向传播:计算当前的代价
3.2 反向传播:计算当前的梯度
3.3 梯度下降:更新参数,更新后的参数为θ_updated=θ−αdθ,其中α是学习率,dθ其实就是dJ/dθ。
直到iteration结束,或者梯度近似为零、参数不再变化为止。
其中sigmoid函数的导数要牢记:sigmoid_derivative(x)=σ′(x)=σ(x)(1−σ(x)),还有两个导数公式:
其代码在前向传播的函数中实现如下:
m = X.shape[1]
A = sigmoid(np.dot(w.T, X) + b)
cost = -np.sum(Y*np.log(A) + (1-Y)*np.log(1-A))/m
dw = np.dot(X, (A-Y).T)/m
db = np.sum(A-Y)/m
为了保证在矩阵计算和broadcasting中不出错,进行如下的断言:
assert(dw.shape == w.shape)
assert(db.dtype == float)
cost = np.squeeze(cost) # 降低cost的维度使其成为一个数
assert(cost.shape == ())
Python
Python Broadcasting
我觉得这一块非常精彩,因为很多tutorial里面只是数语带过,Andrew讲得比较多。在矩阵运算中,如果不注意到broadcasting,出现了bug也不太好调。所以我在这里着重整理一下:
Broadcasting是指在对不同形状的矩阵进行四则运算时,numpy对小矩阵的传播处理(其实就是ctrl-C + ctrl-V,使得小矩阵“长大”成能和大矩阵和谐运算的方法)。具体的说明在这里:矩阵的传播运算。这个功能很便捷,比如在计算np.dot(w.T, X) + b的时候,因为有时候b只是个标量 (scalar),而第一项可能是个矩阵,broadcasting使得这一步计算变得很方便。
>>> a = np.array([1.0, 2.0, 3.0])
>>> b = 2.0
>>> a * b # 在乘法计算时,numpy的矩阵传播机制将b这个标量自动拓展为np.array([2.0, 2.0, 2.0]),使其能与a的每一个元素相乘。
array([ 2., 4., 6.])
比如矩阵的normalization by row,是矩阵除以每一行的norm:
上图的实现方法为:
>>> x_norm = np.linalg.norm(x, ord=2, axis=1, keepdims=True)
>>> x = x/x_norm
其中ord=2表示norm 2,axis=1表示horizontally即每一行 (by row) 的计算,axis=0表示vertically即每一列 (by column) 的计算。keepdims=True是为了防止numpy输出rank 1 array——shape为(n,),使用了keepdims=True后输出的shape是(n,1),这两者之间的不同会在下文中展示。
另一个体现broadcasting高效之处是softmax函数,通常用于标准化多类别分类问题的输出,使得各类别输出的总概率加起来为1。由下图softmax的函数表达可知,分母和原矩阵是不同形状的。分母比原矩阵少一维,即当原矩阵是1*n时,分母是这n个数的和,所以是一个标量;当原矩阵是m*n时,分母是每行n个数的和,所以是一个m*1的矩阵(数组)。broadcasting使得分子直接除以分母就可以得到原矩阵每个数标准化的结果。
softmax的代码为:
>>> x_exp = np.exp(x) # 用numpy的exp而不是math中的exp是因为math包的函数通常只接受实数的输入,而numpy可以接受张量输入,因此在深度学习中,我们很少用math,而多用numpy的方法,前面的log也是同理。
>>> x_sum = np.sum(x_exp, axis=1, keepdims=True)
>>> s = x_exp/x_sum
>>> return s
有了传播机制,当两个矩阵维度相同、或者其中有一个矩阵的一个维度为1的情况下,两个矩阵就可以进行逐个元素的加减乘除运算了。但与此同时,为了减少出bug的可能性,建议多使用assert + shape来检查矩阵的形状,或者用reshape方法。
numpy中的dot、element-wise和outer product(点积、元素积和外积)
1) dot product (点积)
np.dot(A, B)就是普通的线性代数中的矩阵乘法,是按照矩阵乘法的规则来运算的,要求两个矩阵的维度附和线性代数乘法的运算规律。
2) element-wise product (元素积)
np.multiply()和*都是元素积,是数组元素逐个计算。请注意,broadcasting适用于元素积(*)的情况而不是点积。如:
a = np.random.randn(4, 3) # a.shape = (4, 3)
b = np.random.randn(3, 2) # b.shape = (3, 2)
c = a*b会报错,因为b需要是4*1或者3*1的情况才能broadcasting。
c = np.dot(a,b)会得到一个4*2的矩阵。
3) outer product (外积)
numpy的outer product中out[i, j] = a[i] * b[j],即两个一维矩阵a = [a0, a1, ..., aM]和b = [b0, b1, ..., bN]的outer product是:
[[a0*b0 a0*b1 ... a0*bN ]
[a1*b0 .
[ ... .
[aM*b0 aM*bN ]]
>>> import numpy as np
>>> x1 = [9, 2, 5, 0, 0, 7, 5, 0, 0, 0, 9, 2, 5, 0, 0]
>>> x2 = [9, 2, 2, 9, 0, 9, 2, 5, 0, 0, 9, 2, 5, 0, 0]
>>> np.dot(x1,x2)
278
>>> np.outer(x1,x2)
[[81 18 18 81 0 81 18 45 0 0 81 18 45 0 0]
[18 4 4 18 0 18 4 10 0 0 18 4 10 0 0]
[45 10 10 45 0 45 10 25 0 0 45 10 25 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[63 14 14 63 0 63 14 35 0 0 63 14 35 0 0]
[45 10 10 45 0 45 10 25 0 0 45 10 25 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[81 18 18 81 0 81 18 45 0 0 81 18 45 0 0]
[18 4 4 18 0 18 4 10 0 0 18 4 10 0 0]
[45 10 10 45 0 45 10 25 0 0 45 10 25 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
[ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]]
>>> np.multiply(x1,x2) # 或者x1*x2
[81 4 10 0 0 63 10 0 0 0 81 4 25 0 0]
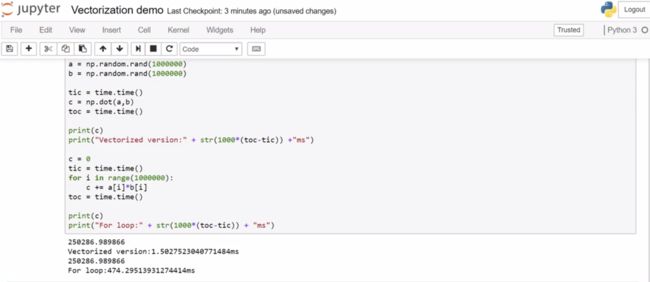
Vectorization
这一部分就是说尽量用矩阵运算而不是for loop。比如在反向传播 (back propagation) 时,计算每一个样本loss function并加成cost function时,以及对每一个参数进行更新时,都用矩阵运算。只不过iteration时得用for loop,这估计是无法避免的了。
* 其中numpy.random.randn(d0, d1, ... dn) 返回的是从标准平均分布中抽样的n维数组。
Numpy应用技巧
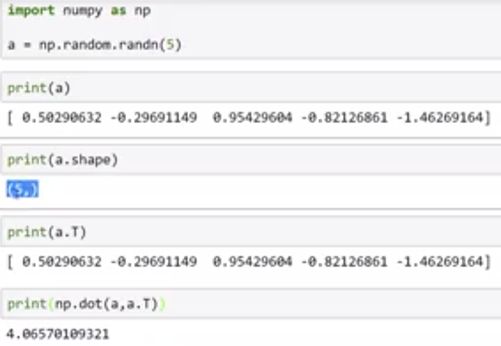
要避免用类似于(5,)这样的rank 1 array,这样的array乍看是一个5*1的matrix,但是在计算中会导致与5*1矩阵完全不同的结果。避免的方法是在定义时设定好维度或reshape方法,或者在计算时用多assert + shape的检查。
如果输入是np.random.randn(5, 1) 的时候,输出的结果就完全不同,尽管a.T上去是一样的。
因为篇幅限制今天就先写到这里,感兴趣的朋友们可以关注我的《吴恩达Coursera Deep Learning学习笔记 1 (下)》。在这里引用萌萌哒Andrew的话与君共勉:
In the CS world, all of us are used to needing to jump every ~5 years onto new technologies and paradigms of thinking (internet->cloud->mobile->AI/machine learning), because new technologies get invented at that pace that obsolete parts of what we were previously doing. So CS people are used to learning new things all the time.
在 CS 世界中,我们所有人都习惯于每 5 年就要跳到新技术和思维模式(互联网→云→移动→AI/机器学习),因为新技术以这样的速度发明。所以,CS 人也一直习惯于不断学习新的事物。