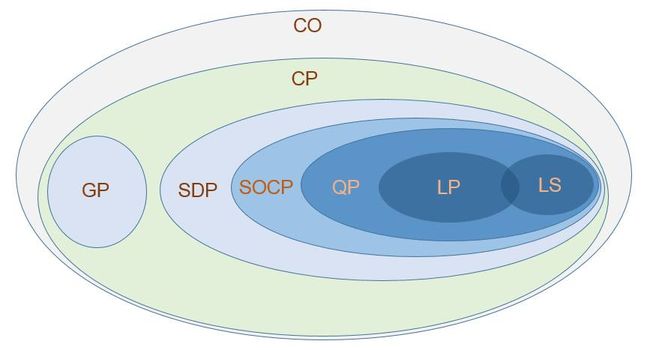
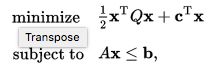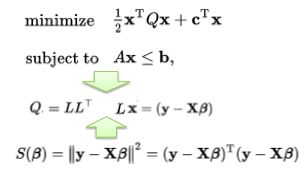一般来说凸优化(Convex Optimization, CO)中最一般的是锥规划 (Cone Programming, CP)问题, 前面我们介绍了点最小二乘(Least Square, LS)和线性规划(Linear Programming, LP)问题, 现在我们介绍一点二次规划(Quadratic Programming)。
引子
Joseph-Louis Lagrange 拉格朗日是变分法(calculus of variations)的建立者之一, 变分法是自微积分发明以后一个重大突破, 对应到离散算法领域,动态规划(dynamic programming)可以看成是一种变分法。 拉格朗日出生于意大利政府官员家庭, 但是他爸本该留下大笔财富,但是却经营不善, 家道衰落。 于是他爸想让他成为律师, 他从小最喜欢的课程是拉丁文, 对几何有点厌恶。 直到17岁, 他读了天文学家Edmond Halley 哈雷的一片论文, 发现里面有些地方看不完全明白, 就这样迷上了数学, 然后整整1年沉浸在数学之中, 1年后, 他由于数学才华, 而被本地公爵任命为助理教师, 来给部队讲解如何应用Leonhard Euler欧拉的学术来研究弹道理论(ballistics theories)。 从此一发不可收拾踏上微积分的不归路。拉格朗日后期的成就离不开与欧拉的广泛交流和提拔。
对此, 我想说的是,不喜欢文学,历史,天文学的数学家不是一个好数学家。 其次,1年在新方向的学习,足以改变一生的命运, 所以当你希望改变时候, 你就在一个新的感兴趣的领域坚持一年的沉浸。 再次,数学不要深入的太早,14岁之前还是练练记忆力吧。
随便说一下, 拉格朗日身体一直一般, 但是骗妹妹的水平还是不错的, 第一个老婆是他一个远房的侄女, 但是她身体也不好, 不久就去世了。 第二个老婆是他好友的女儿, 在一片反对声中, 她嫁给了他。 另外, 拉格朗日做人也是相当有一套, 中庸之道学的很好, 他见证了法国各种革命,每次都继续被重用, 但是没有人想过要伤害他。 他的信条之一就是,我是个小心的外来者, 我得恪守这里的规矩。 对比,他的好友, 大化学家拉瓦锡, 就不幸被处决了。
这次描述的二次规划, 简直就是见证拉格朗日奇迹的旅程。 不管是内值法(interior point),增强拉格朗日法, 还是对偶问题(duality)都离不开拉格朗日。
QP,二次规划概述
在1940年左右(1939年 Leonid Kantorovich总结发表了线性规划), 线性规划LP被提出来, 10年后, QP作为Non-Linear Programming, NLP被总结发表。
顾名思义, 二次规划就是把一次规划(线性规划, LP)的目标公式扩展到二次函数:
这里 Q 是对称矩阵(Symmetric Matrix)
那么这样修改目标之后, 会带来什么改变?
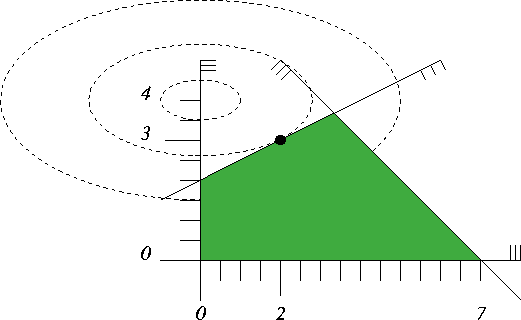
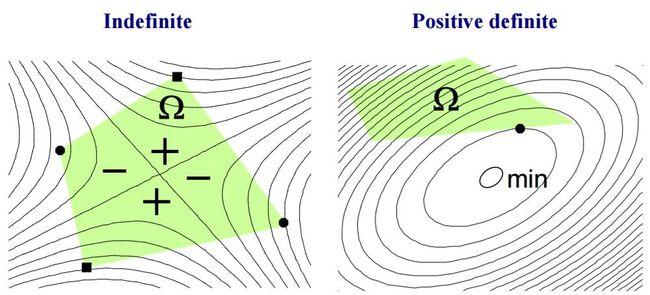
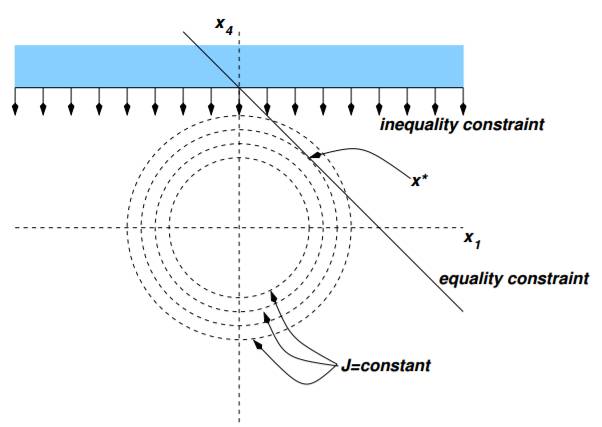
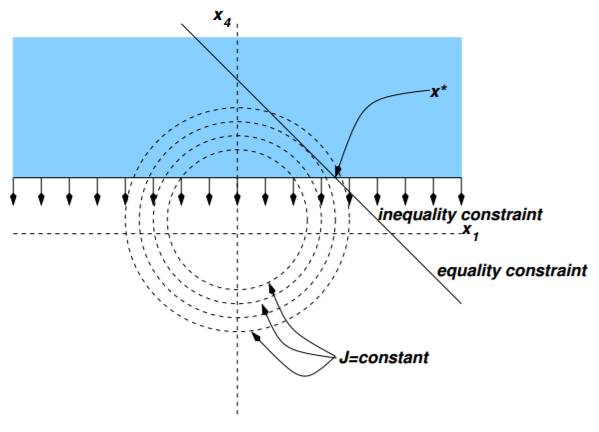
首先从图上来看, 最大的变化就是二次带来等高线(contour line )不再是直线, 这样使得最值点不再是限制多面体的角上,可能是边上,或者内部。
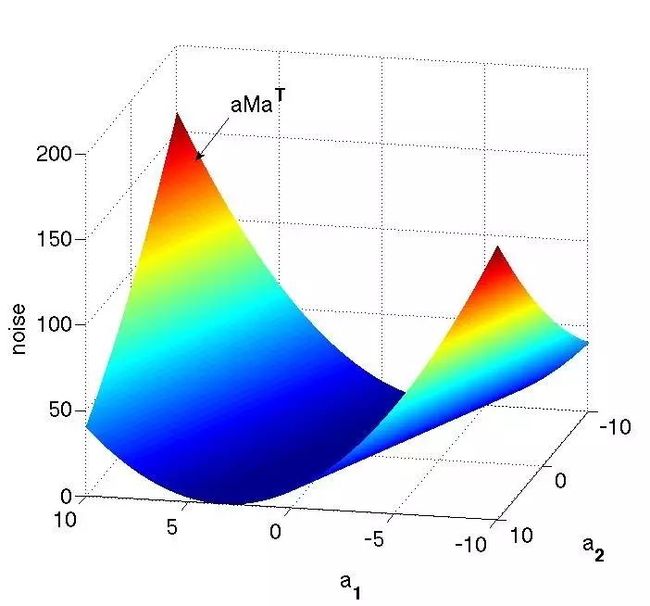
我们来看一下,三维立体的情况:
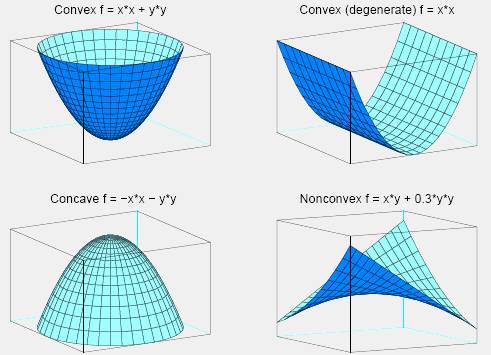
另外, 一般来说, 二次关系带来的还可能是凸和非凸情况产生:
但是对于非凸的情况下, 对应的对称阵是一个不定矩阵(indefinite), 但是对于凸的情况下, 对应的对称阵是一个正定矩阵(positive-definite)。
同时, 这样改变之后有什么好处?
QP第一次统一了LP和LS, 前面我们提到, 当利用不同的距离公式的时候,最优回归参数,可能是LS的情况, 也可能是LP情况。
欧式距离: 最小二乘法,LS
Hamitton 距离,或者Chebyshev距离: 线性回归,LP
这样,基于利用QP就可以统一描述不同距离公式下的回归的参数求解。
前面, 我们说了QP是LP和LP在不同角度的扩展:
1.QP是LP的扩展, LP是QP在二次项系数为0时候(Q=0)的特例。
2.QP是LS的扩展, LS是QP在一次项系数为0, 二次项系数为I(单位阵),并且没有限制的时候的特例:
所以, QP是把LS的二次项对称单位阵扩展到任意对称阵Q, 再加上LP的一次项。因为Q是对称矩阵(symmetric matrix),利用矩阵分解Q = LL^T, 那么QP的二次项可以看成特殊的最小二乘法:
这样我们描述了QP作为LP和LS一般性扩展(特例)的意义
再进一步,为什么要有QP?
依然从LS和LP的扩展说起:
1. Constrained LS 依赖于QP:
2. Randomized LP 依赖于QP:
这样我们描述了QP作为LP和LS必要性扩展的意义
QP 求解概述
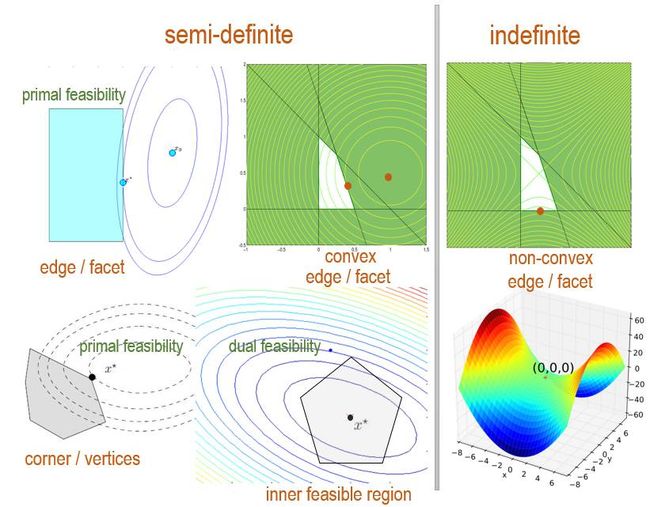
在求解之前, 我们先看一下, 求解大概会遇到哪些情况?如下图, 不管semi-definite,还是indefinite的情况下, 大部分情况(大致有如下4种情况), 最值点是分布在feasible region的边界上, 但是在definite情况下, 可能最是内部最值点。
QP怎么求解的?
一般来说, QP的求解主要有两大方面的限制(如下图所示):
首先是Q矩阵, Q矩阵是不是半正定(Semi-Definite)的, 如果不失意味着, 目标函数是非凸(non-convex)的情况。
其次是条件关系, 是不是全部是等式(eqality-constrained), 如果是的话, 就是一个可以直接求解的KKT系统(KKT System), 否则的话,就是一般情况下的Convex QP问题。
KKT 系统是什么?
什么是KKT呢?KKT是3个人的姓的首字母, 分别是Karush, Kuhn和Tucker, 更多细节参考 “一挑三, FJ vs KKT”。
前面我们说了KKT系统是利用KKT条件进行求解的,(in)-equality constraint情况下的Convex QP求解方式。
常见的解法包括:
Direct solution of the KKT system
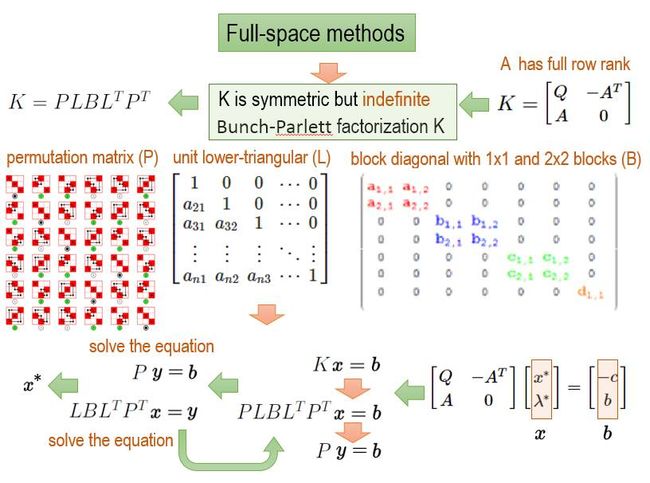
Full space method
Range space method
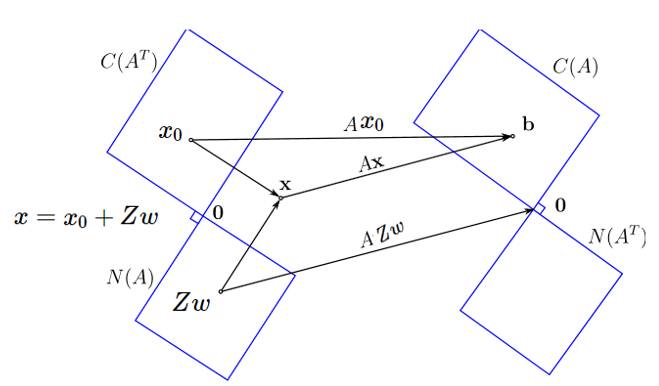
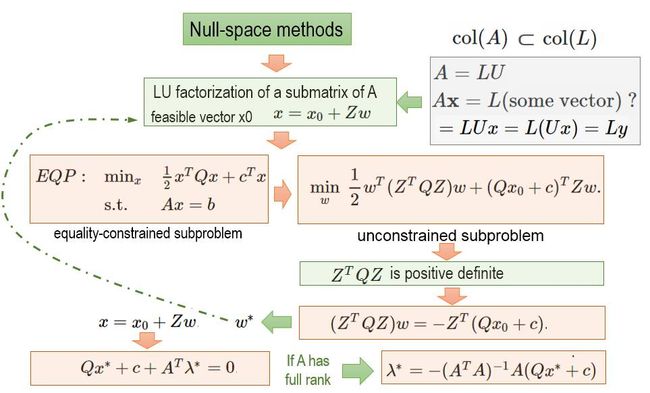
Null space method
Active set strategies
Interior-point methods
Central path method
Logarithmic barrier functions
Direct solution of the KKT system
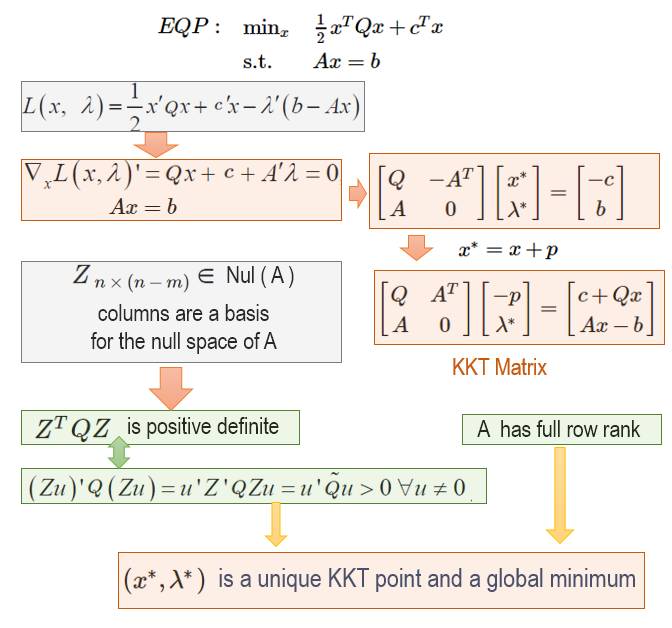
如果目标公式是一个equality-constrainted quadratic programming,EQP。 我们可以直接利用KKT System进行求解。
KKT System 是利用KKT条件进行建模求解, 然后构建一个KKT矩阵matrix的系统。
KKT Matrix 是巧妙的构建的一个对称矩阵(Symmetric)矩阵。
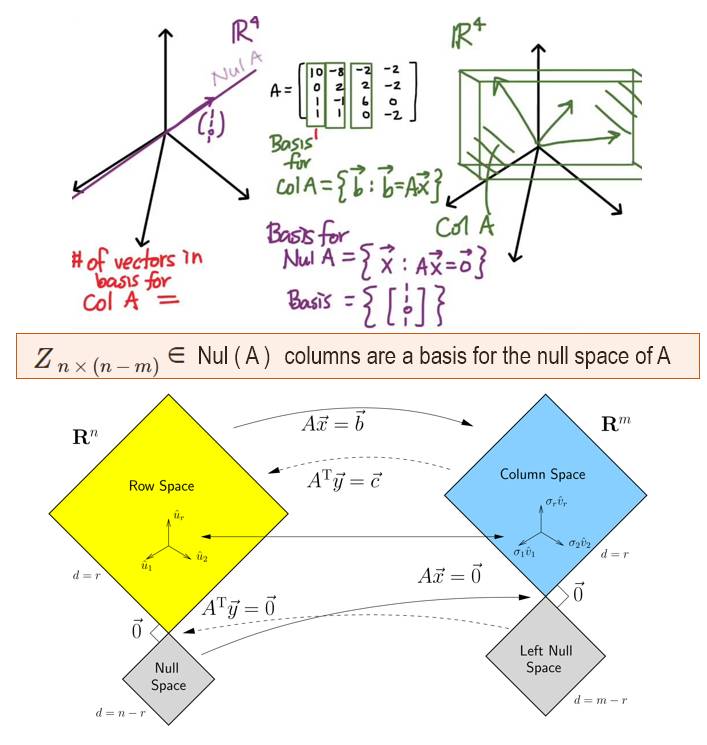
这里要注意的时候, 这里Z是A矩阵的零空间null space的基。 更多关于Null Space的细节,请参考“矩有四子”。
根据KKT条件, 我们知道,A是満秩 (full rank)矩阵, 并且Z'QZ是正定(positive definite), 那么是一个凸系统(更多细节参考 “一挑三 FJ vs KKT”), 那么可以知道存在唯一全局最优解(global optimum)。
如果Q是对称symmetric的!
如果Q是正定,而且很容易求逆!
如果A容易实现LU分解LU factorization!
我们把x分解到Col(A)和Nul(A), (更多关于Null Space的细节,请参考“矩有四子”)。这样我们得到:
由于我们知道b是固定的, 那么这种分解之后, x0就是固定的了。
这样, 我们就可以求解到最佳的w*。
这样我们解释了直接利用EQP问题的KKT System进行求解, 并且分析了Range-space method和Null-space method的适用情况。