Motivation:
步态可被当作一种可用于识别的生物特征在刑侦或者安全场景发挥重要作用。但是现有的方法要么是使用步态模板(能量图与能量熵图等)导致时序信息丢失,要么是要求步态序列连续,导致灵活性差。这篇文章是将步态当成包含独立帧的集合,不要求帧的排列顺序甚至可以把不同场景下的视频帧整合在一起。
Method:
问题定义:给定一个有N个人的数据集$y_{i}, i \in 1,2,...,N$, 我们假定某个人的步态遮罩属于分布$\mathcal{P}_{i}$,这是个只与行人身份有关的量。因此,某个人的一个或者多个序列的所有遮罩可以视为$n$个剪影的集合$\mathcal{X}_{i}=\left\{x_{i}^{j} | j=1,2,...,n\right\}$。这里的$x_{i}^{j} \sim \mathcal{P}_{i}$。
在前面这种假设下,我们通过三步解决步态识别任务,可以公式化为:
$f_{i}=H\left(G\left(F\left(\mathcal{X}_{i}\right)\right)\right)$
这里的$F$是一个用来提取帧级特征的卷积神经网络。公式$G$是一个置换不变函数来将frame-level特征变成set level特征,具体是通过下面提到的$Set Pooling$来实现的。$H$则是从set-level特征中提取有区分力的表达$\mathcal{P}_{i}$,是通过$HPM$(水平金字塔映射)实现的。输入$\mathcal{X}_{i}$则是一个四维张量,也就是set维,通道维,高度,宽度。
放一张网络框架图:
Set Pooling:
Set pooling的目的是将集合中的步态信息整合在一起,也就是$z=G(V)$,这里$z$表示set-level特征,$V=\left\{v^{j} | j=1,2, \ldots, n\right\}$表示frame-level特征。Set Pooling接收set作为输入,是一个排列不变函数,公式化为:
$G\left(\left\{v^{j} | j=1,2, \ldots, n\right\}\right)=G\left(\left\{v^{\pi(j)} | j=1,2, \ldots, n\right\}\right)$
这里的$\pi$是任何一种排列。因为现实场景下,人物步态遮罩数目是任意的,函数$G$应该能够处理任意任意基数的set。
1.统计函数:为了满足前面的要求也就是排列不变,数目容量可变,在set维使用统计函数是一个自然的选择。本文是使用了$max()$,$mean()$,$median()$三种。
2.联合函数:也就是前面三者的结合,可以分为两种:1)$G(\cdot)=\max (\cdot)+\operatorname{mean}(\cdot)+\operatorname{median}(\cdot)$,2)$G(\cdot)=1_{-} 1 \mathrm{C}(\operatorname{cat}(\max (\cdot), \operatorname{mean}(\cdot), \operatorname{median}(\cdot)))$。
这里cat表示的是通道维拼接,$1_{-} 1 C$表示1*1卷积。
作者也使用了注意力机制来提高SP的表现,motivation是利用全局信息来学习元素级注意力图来修正frame-level特征。全局特征先通过左侧的统计函数获取,之后将它输入进$1*1$卷积层同原始特征图计算注意力。最终的set-level级特征是通过在修正后的全局特征上应用MAX得到。采用了残差结构来加速与稳定收敛。
水平金字塔映射(HPM):
在行人重识别任务中经常把特征划分为水平块,这里也是借鉴了这个做法。$HPM$有4个不同尺寸能够帮助神经网络聚焦到不同的局部特征和全局特征。下图描述得比较清楚,假设共有$S$个尺寸,在s这个尺寸,特征在高度维上进行切分被分成了$2^{s-1}$块,所以总共是可以分成$\sum_{s=1}^{S} 2^{s-1}$块。接着利用全局池化($Global Pooling$)来将划分得到的$3D$块变成$1D$的$f^{\prime}$。最后对$f^{\prime}$使用不同的$FC$层做映射得到有区分力的$f$。
Multilayer Global Pipeline :
简单来说越深的层有着越大的感受野,浅层关注的是局部和精细化特征,而深层关注全局和粗粒度特征。同理不同深度上SP得到的特征也是有这个特性的。为了利用不同深度的特征就提出了Multilayer Global Pipeline(MGP),和主pipline的流程是差不多的,就是把不同层的set-level特征加到MGP中。最后MGP也是通过前面的HPM划分为$\sum_{s=1}^{S} 2^{s-1}$个块。MGP后面的HPM和主pipline的HPM是不共享参数的。
训练和测试:
训练损失:网络的输出是$2 \times \sum_{s=1}^{S} 2^{s-1}$的d维向量。在这里使用的是批三元损失。使用了$p \times k$的采样策略。$p$是人物数,$k$是一批中每个人的样本数,这里的每个样本其实包含了从序列中采集的多个遮罩图。
测试:给定查询$\mathcal{Q}$,步态识别的目标是从图库集合$\mathbb{C}$中查询获得该人物所有序列。测试时先将$\mathcal{Q}$输入到GaitSet产生多种尺寸的特征然后concatenate到一起获得最终表达$\mathcal{F}_{\mathcal{Q}}$。同理我们对图库中的样本$\mathcal{G}$也进行这个操作得到$\mathcal{F}_{\mathcal{G}}$。最后计算$\mathcal{F}_{\mathcal{Q}}$与每个$\mathcal{F}_{\mathcal{G}}$的欧式距离作比较计算Rank 1识别率。
实验:
从作者的消融实验来看,其提出的几个模块是有效果的。带来效果比较突出的是使用set作为输入,以及使用独立FC和不同深度特征融合这几大点。
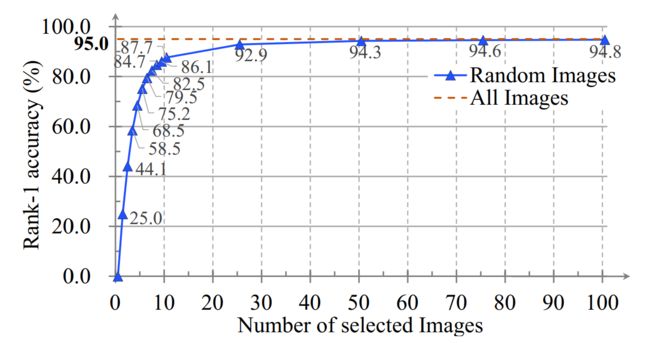
作者做了几个有意思的实验,一个是遮罩数目对识别准确率的影响,可以看到1)精度随着轮廓数量的增加而单调增加;2)当样本包含25个以上轮廓时,精度接近最佳性能。这个数字与一个步态周期包含的帧数一致。
下面的实验是将不同视角的遮罩放在一起组成查询(图库不变),比如第二行前几列是从两个相差一定角度间隔的序列中各采样5张,而最后一列Sigle view是从单个序列中选择10张。可以看到多视角的更好一点,这表明改模型能够利用多视角带来的平行以及垂直信息。
作者同时还做了不同行走条件的影响,结果如下所示,表明增加遮罩数是可以带来效果提升的,即使是背包或者穿大衣这种带有噪声的遮罩。