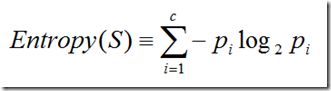By RaySaint 2011/07/08
决策树
决策树可以说是用的非常广泛的学习算法,对噪声数据有很好的健壮性,而且表达能力也很强(机器学习读书笔记(二)中的候选消除算法只能表示属性的合取,决策树可以表示属性的析取)。虽然决策树不是最好的学习算法,但是目前最牛哄哄的几个学习算法,如boosting和随机森林(Random Forest)在内部都使用了决策树,因此很有必要深入了解一下决策树。
简介及决策树表示法
在《机器学习》By Mitchell书中讲到决策树是一种逼近离散值目标函数的方法,也就是说决策树适用于分类(classification)问题,事实上,决策树也可以用来做回归(regression),例如有名的CART(Classfication and Regression Tree,分类与回归树)系统(由Friedman和Breiman两个大牛提出来的)。这里还是主要讲如何使用决策树学习来解决分类问题。
下面的图是一个通常的决策树表示:
由于以树的形式表达,决策树的一个优点就是让人一目了然,也很符合人的思维习惯(人在做某个决定时,总会将一系列需要考虑的”因素”按某种重要性准则先排个序,然后优先考虑该因素)。图上是一个根据天气情况分类“星期六上午是否适合打网球“的决策树,每一个非叶子节点都指定了对待分类实例的某个属性的测试(如Outlook表示测试天气预报的情况,即询问天气预报的情况是晴天Sunny,阴天Overcast,还是下雨Rain?),并且该节点的每一个后继分支对应于该属性的一个可能值;每一个叶子节点即为实例所属的分类。分类实例的方法就是从树的根节点开始,测试这个节点指定的属性,然后按照给定实例的该属性值对应的树枝向下移动。然后这个过程在新节点为根的子树上重复,直到到达叶子节点。
举一个例子,假设实例的表示形式为
这里要注意,上图中的树为一棵多叉树,节点的后继分支数由节点上测试属性取值的个数决定。然而在计算机中,多叉树比较难于表示,而二叉树易于表示,且二叉树有很多优良的属性,因此在编写程序时,一般以二叉树的形式来表示决策树,称为二叉决策树,也就是上面提到的CART系统。
本质上,决策树代表实例属性值约束的合取的析取式。从树根到树叶的每一条路径对应一组属性测试的合取,树本身对应这些合取的析取。例如上图表示的决策树对应于以下表达式:
(Outlook = Sunny ∧ Humidity = Normal) ∨ (Outlook = Overcast) ∨ (Outlook=Rain ∧ Wind = Weak)
决策树学习的适用问题
通常决策树学习最适合具有以下特征的问题:
1.实例是由“属性-值”对表示的:实例是用一系列固定的属性和它们的值来描述的(如上面的例子中的x)。最简单的决策树学习中,每一个属性只取少数的离散的值(例如,Temperature取Hot、Mild和Cold)。然而,很容易扩展到也允许处理值域为实数(连续值)的属性。
2.目标函数具有离散的输出值,也就是说要解决的问题是一个分类问题。实际上,如一开始讲述的,决策树也可以用来做回归问题。
3.可能需要析取的描述。
4.训练数据可以包含错误。决策树对于噪声有很好的健壮性。无论是目标值属性的错误(即分类错误)还是描述属性错误。
5.训练样例可以包含缺少属性值的实例:决策树学习甚至可以在有未知属性值的训练样例中使用。这个问题后面会进行讨论
理解决策树算法思路的关键是决策树的归纳偏置(归纳偏置的概念参见机器学习读书笔记(二),它是学习算法的一个重要特征),这个偏置被称为奥坎姆剃刀(occam’s razor)。
基本的决策学习算法
大多数已开发的决策树学习算法是一种核心算法的变体。该算法采用自顶向下的贪婪搜索遍历可能的决策树空间。这种方法是ID3算法(Quinlan 1986)和后继的C4.5算法(Quinlan 1993)的基础。下面给出经典的ID3算法的概要:
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
ID3(Examples, Target_attribute, Attributes)
输入:
Examples即训练样例集。Target_attribute是这棵树要预测的目标属性。Attributes是除目标属性外供学习到得决策树测试的属性列表。
输出:
返回一棵能正确分类给定Examples的决策树
伪代码表示:
{
创建树的Root节点
if(Examples 都为正) // 决策树增长终止条件
返回label = + 的单节点树Root
if(Examples 都为反) // 决策树增长终止条件
返回label = - 的单节点树Root
if(Attributes为空) // 决策树增长终止条件
那么返回单节点树Root, label=Examples中最普遍的Target_attributes值
A <- Attributes中分类Examples能力最好的属性
Root的决策属性 <- A
foreach (a in A) // a为属性A的每个可能取值a
{
在Root下加一个新的分支对应测试A = a
令Examples(a)为Examples中满足A属性值为a的子集
在这个新分支下加一个子树ID3(Examples(a), Target_attribute, Attributes - {A})
}
返回Root
}
////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
算法的过程并不复杂,就是不断选取某个属性对样例集划分直到决策树增长终止条件满足为止。终止条件为:
1. 节点是一个纯节点,即从某一分支到达该节点上所有的样例(这些样例满足分支上的属性测试的值)属于同一个分类。
2. 所有属性都已经被作为测试属性使用过了。
总之,上面的算法就是一种自顶向下增长树的贪婪算法,在每个节点选取最好地划分样例的属性。继续这个过程直到这棵树完美分类训练样例,或所有的属性都已被使用过。
现在有一个重要的问题是:如何选择在树的每个节点要测试的属性?这里顶一个统计属性,称为信息增益,它用来来衡量给定的属性区分训练样例的能力。
熵和信息增益
什么样的属性才是最好地分类样例的属性?直觉上讲,如果训练样例集被某个属性A划分,得到的所有子样例集(每个子样例集中的子样例满足A的某个取值a)如果都是“纯净”的,也就是说各个子样例集中的子样例(根据目标属性的取值)都属于同一个分类,那么这个属性A绝对是对能够最好的区分样例的属性(因为只要用这个属性对样例测试,那么就可以得到分类的结果)。也就是说,根据某个属性对样例集进行划分后,得到的子样例集越”纯净“,那么这个属性对样例集的区分能力越强。
注意,这里不是很严谨,上面一段话中前后两个“纯净”并不是相同的含义。第一个”纯净”是一个二值判断,如果样例集中的子样例都属于同一个分类,那么样例集就是纯净的,反之则是不纯净的。上面一段话中第二个“纯净”是一种程度的描述,把它称为样例集的纯度(也就是说第一个“纯净”是第二个“纯净”的特例,或者说极端情况)。这里把比较两个属性对样例集的区分能力转化为比较使用两个属性对样例集划分后得到的子样例的纯度。
如何刻画样例集的纯度呢?这里引入信息论中广泛使用的一个度量标准,称为熵(entropy)。给定样例集S,目标属性有c个不同的值,那么S相对于这c个分类的熵定义为:
在熵的计算中,我们定义0log0为0。
上式中,pi是S中属于类别i的比例。举一个例子:假设S是一个关于某布尔概念(目标属性的取值有2个,“+”和“-”表示正样本和负样本)的有14个样例的集合,它包括9个正例和5个反例(我们采用记号[9+,5-]来概括这样的数据样例)。那么S相对于这个布尔分类的熵为:
Entropy([9+, 5]) = –(9/14)log(9/14) – (5/14)log(5/14) = 0.94
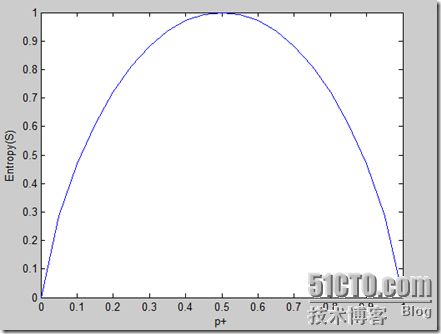
注意,如果S的所有成员属于同一类,那么S的熵为0。如果S中的正反样例的数量相等时,熵为1。下面的图刻画了布尔分类的熵函数随着p+(正样例占总样例的比例)从0到1变化的曲线
从上面的图可知道也就是说样例集越“纯”的时候(对应途中横轴两边的情况),熵越小。这个结论可以由只有两个分类的情况推广到有多个分类的情况。
(信息论中的熵可以解释为用二进制位0和1对某个信息(如字串)进行编码所需的二进制位的长度,样例集越纯的时候,其中包含的信息越少,因此要编码样例集的目标值的时候所需的二进制位越少,熵就越小。对于熵的更详细解释会在后面讲到贝叶斯学习时给出)
有了这个结论之后,我们就可以衡量属性对于样例的区分能力了。用某个属性划分样例集后,每个样例子集越“纯净”,那么该属性对于样例的区分能力就越高,这样每个子集的熵就越小,这些子集组成的整个样例集的期望熵也就越小,也就是期望熵相对于原样例集(在未用该属性划分样例前)的熵降低地越多。这个熵降低的大小就称为信息增益。
因此,要求出信息增益,首先求出样例集S在划分前的熵Entropy(S);然后,样例集S被某个属性A划分为多个子集,求出每个子集S(a)的熵Entropy(S(a)),并求出样例集S被属性A划分后熵的期望∑|S(a)|/|S|*Entropy(S(a));最后用Entropy(S) - ∑|S(a)|/|S|*Entropy(S(a))得到由于使用这个属性划分样例导致的期望熵降低,这个就是一个属性A相对于集合S的信息增益Gain(S,A)。下面给出精确定义:
注意,等式右边第二项描述的期望熵就是每个子集的熵的加权和,权值为属于S(a)的样例占原始样例S的比例。
再次强调,信息增益Gain(S,A)是由于知道属性A而导致的期望熵的减少。换句话讲,就是给定属性A,得到的关于目标函数(如何分类样例)的信息量,或者说是知道属性A的值后对S的任意一个成员的目标值进行编码时,可以节省的二进制位数。
决策树学习中的假设空间搜索
机器学习读书笔记(一)中提到过,任何一个归纳学习算法可以被描述为从一个假设空间(称为知识的表示)中搜索(称为搜索策略)一个拟合训练样例的假设。上面提到的ID3算法搜索的假设空间就是可能的决策树的集合。ID3算法一种从简单到复杂的爬山算法遍历这个假设空间,引导这种爬山搜索的评估函数是信息增益度量。
通过观察ID3算法的搜索空间和搜索策略,可以深入认识这个算法的优势和不足。
ID3算法中的假设空间包含所有的决策树,它是关于现有属性的有限离散值函数的一个完整空间。因为每个有限离散值函数可被表示为某个决策树,所以ID3算法避免了搜索不完整假设空间的一个主要风险:假设空间不包含目标函数。
当遍历决策树空间时,ID3仅维护单一的当前假设。因为仅考虑单一的假设,ID3算法失去了表示所有一致假设所带来的优势(这个与机器学习读书笔记(二)中变型空间的候选消除算法不同,候选消除算法维护了与当前的训练样例一致的所有假设的集合)它不能判断有多少个其他决策树也是与现有的训练数据一致的。
基本的ID3算法在搜索中不进行回溯。每当在树的某一层次选择了一个属性进行测试,它不会再回溯重新考虑这个选择。所以,它易受无回溯的爬山搜索中的常见风险影响:收敛到局部最优的答案,而不是全局最优的。后面会讨论一个扩展,增加一种形式的回溯(后修剪决策树)
ID3算法在搜索的每一步都使用当前的所有训练样例,以统计为基础决定怎样精化当前的假设。使用所有样例的统计属性(例如信息增益)大大降低了对个别训练样例错误的敏感性。因此,通过修改ID3算法的终止准则以接受不完全拟合训练数据的假设,他可以被很容易地扩展到处理含有噪声的训练数据。
决策树学习的归纳偏置
回忆机器学习读书笔记(二)中提到的,归纳偏置是一系列前提,这些前提与训练数据一起演绎论证未来实例的分类。
要描述ID3算法的归纳偏置,应找到它从所有一致的假设中选择一个的根据。ID3选择在使用简单到复杂的爬山算法遍历可能的树空间时遇到的第一个可接受的树。从上面的描述可知道,ID3的搜索策略为:
(a)优先选择较短的树而不是较长的。(由简单到复杂的自顶向下的贪心算法决定)
(b)选择那些信息增益高的属性里根节点较近的树。(由信息增益的属性选择度量决定)
上面的两点决定了ID3算法的归纳偏置,注意,它们并没有先后顺序,而是存在一种微妙的相互作用的关系,也就是说,虽然较短的树优先与较长的树,但ID3算法并不是总是选择最短的树,而又倾向于那些信息增益高的属性更靠近根节点的树,因此准确刻画ID3归纳偏置是很难的。下面给出一个近似的刻画。
ID3归纳偏置的近似:较短的树比较长的树优先。那些信息增益高的属性更靠近根节点的树优先。
ID3算法的和第二章中讨论的候选消除算法显示出的归纳偏置之间有一个有趣的差别。
1.ID3算法的假设空间是一个完整的假设空间,从ID3的归纳偏置可知,它不彻底搜索这个空间,而是从简单的假设到复杂的假设,直到遇到终止条件。因此ID3的归纳偏置完全是搜索策略排序假设的结果。
2.变型空间的候选消除算法的搜索范围是不完整的假设空间(只搜索由属性的合取表示的假设),但它彻底搜索这个空间,查找所有与训练样例一致的假设。它的归纳偏置完全是假设表示的表达能力的结果。
总结一下,ID3算法的归纳偏置来自它的搜索策略,该策略假定某种假设胜过其他假设(较短的假设比较长的更优),因此称这种归纳偏置为优选偏置(preference bias)或搜索偏置(search bias)。相反,候选消除算法的偏置是对待考虑假设的一种限定。这种形式的偏置通常称为限定偏置(restriction bias)或语言偏置(language)。
通常,优先偏置比限定偏置更符合需要,因为它保证了位置的目标函数被包含在学习器工作的假设空间中(要不然很可能白忙活一场)。但在实际中,综合使用两者的学习系统是很常见的(例如使用最小均方差(优选偏置)的以线性函数(限定偏置)来表示评估函数的问题)。
奥坎姆剃刀
上面有一个很重要的问题没有讨论,也是你最可能产生疑惑的地方:ID3算法中优选较短决策树的归纳偏置,是不是从训练数据中泛化的一个可靠基础?
有趣的是,这是一个争论很久的哲学问题,威廉·奥坎姆对于此问题提出了一个论点(据说是刮胡子时想到的,牛人就是牛,刮胡子也在想哲学问题),这个论点称为奥坎姆剃刀:
优先选择拟合数据的最简单的假设
上面的一个表述是该理论用在机器学习的场合中的解释。实际上原意是当你有两个处于竞争地位的理论能得出同样的结论,那么简单的那个更好。为什么这个奥坎姆剃刀是正确的呢,《机器学习》By Mitchell这本书在第三章给出一个不是让人很信服的解释,而且通过举了一个模拟进化的群体的例子给出一个相当玄奥的论点:
进化产生的内部表示使得学习算法的归纳偏置称为自我实现的预言,只因为它改变内部表示比改变学习算法更容易。
反正我是没搞清楚这句话到底是啥意思,文章《贝叶斯、概率分布与机器学习》和文章《数学之美番外篇:平凡而又神奇的贝叶斯方法》中对奥坎姆剃刀解释的比较通俗易懂,而且很清楚。大致的意思是奥坎姆剃刀其实是一种模型(假设)选择,它砍掉了复杂的模型,选择了简单的模型,理由是那些简单的模型是先验概率比较高或者似然概率比较高的模型,关于这一点会在以后的贝叶斯学习中详细地介绍。
在ID3算法中,我觉得奥坎姆剃刀是这样发挥作用的:一棵节点比较多(较长的)的复杂的树通常会对训练数据过拟合(Overfit,这个后面还会解释),因此在这棵复杂的树成立的前提下,出现给出的训练数据的可能性会很小;而如果一棵较短的简单的树拟合现有的数据,在这棵简单的树成立的前提下,出现给出的训练数据的可能性比较大。因此简单的树成立的条件下出现给出的训练数据的似然概率大,因此优先选择简单的树。
决策树的过度拟合和后修剪
ID3算法增长树的每一个分支的深度,直到恰好能对训练样例完美地分类。这种做法在训练数据含有噪声时就出现了一个问题,学习器把噪声也当作正确数据学习了,这样得到的假设最后很可能对未来的数据进行错误的分类,而导致实际分类的错误率上升。
对于一个假设,当存在其他的假设对训练样例的拟合比它差,但事实上在实例的整个分布上表现却更好时,我们说这个假设过度拟合(Overfit)训练样例。
下面的图给出了决策树的规模和决策树的预测精度的关系曲线来解释过度拟合。
从图中可以看出,随着树的增长,在训练样例上的精度是单调上升的。然而,在独立的测试样例上测出的样例先上升后下降。也就是,当树的节点逐渐增多是,虽然更加完美的解释了训练数据,但同时也解释了训练数据中的噪声,而这个导致了在测试数据上精度的下降。
因此,为了避免决策树学习中的过度拟合问题,应该减少树的节点个数,降低树的深度。通常通过两种方法:
(1)及早停止树增长。
(2)通过后剪枝减少决策树的节点的个数。
尽管上面第一种方法可能看起来更直接,但是对过度拟合的树进行后修剪被证明在实践中更成功。这是因为在第一种方法中精确的估计何时停止树增长很困难。
后剪枝的方法很多,这里讨论一种发现高精度假设的非常成功的方法,称为“规则后修剪”(rule post-pruning)
它的步骤包括:
(1)从训练集合推导出决策树,增长决策树直到尽可能好地拟合训练数据,允许过度拟合发生。
(2)将决策树转化为等价的规则集合,方法是为从跟节点到叶子节点的每一条路径创建一条规则。
(3)通过删除任何能导致估计精度提高的前件(preconditions)来修剪(泛化)么一条规则。
(4)按照修剪过的规则的估计精度对它们进行排序,并按这样的顺序应用这些规则来分类后来的实例。
例如,一开始图中给出的决策树中最左的一条路径被转化为规则:
IF (Outlook = Sunny) ∧ (Humidity = Normal)
THEN PlayTennis = No
接下来,通过删除不会降低估计精度的先行词来修剪每一个规则。对上面的规则,规则后修剪算法会考虑先行词(Outlook = Sunny) 和 (Humidity = Normal) 。它会这些修剪步骤中使估计精度有最大提升的步骤,然后考虑修剪第二个前件作为进一步的修剪步骤。如果某个修剪步骤降低了估计的精度,那么这个步骤将不会被执行。
注意,估计规则精度使用的验证数据集合是与训练数据集合不相交的。
参考资料
《机器学习》By Mitchell
《贝叶斯、概率分布与机器学习》
《数学之美番外篇:平凡而又神奇的贝叶斯方法》