动态规划之矩阵路径问题

找到大问题和小问题之间共有的特性，列出一定的状态转移规律，然后设计满足条件的小问题解决方案，最后凭借记忆中的中间值快速求出最终解

动态规划的矩阵路径问题是常见的动态规划问题之一，这类题和一般的动态规划问题的解题思路是一样的，存储中间状态并利用这些中间状态去解决最终的问题。但这类问题的边界条件是需要注意的，因为不同类型的矩阵题目会有具体的边界限制，需要细心的寻找。

矩阵的最小路径和

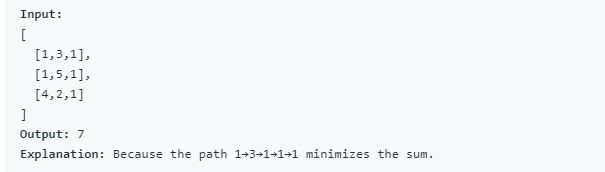
Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.

Note: You can only move either down or right at any point in time.

Example:

 

看到题目，首先是路径和，这样我们就可以定义个dp[][]来存储中间步骤的最小路径和，比如dp[i][j]如果它不是边界的点，那么他的最小路径为min(dp[i-1][j]+grid[i][j],dp[i][j-1]+grid[i][j])，如果他是边界的点但不是初始点，那么他的最短路径就是前一个点的最短路径加上本地的值，初始点呢就是自己的值，这样我们就可以得到代码如下：

    private int[][] dp;
    private int minPathSum(int[][] grid){
        if(grid == null) return 0;
        dp = new int[grid.length+1][grid[0].length+1];
        for (int[] g : dp){
            Arrays.fill(g, -1);
        }
        for(int i = 1 ; i <= grid.length ; i++){
            dp[i][0] = 0;
        }
        Arrays.fill(dp[0], 0);
        return helper(grid, grid.length, grid[0].length);
    }
    private int helper(int[][] grid, int i, int j){
        if(dp[i][j] != -1) return dp[i][j];
        /**
         * 边界判定
         */
        if(i > 1 && j > 1)
            dp[i][j] = Math.min(helper(grid, i-1, j) + grid[i-1][j-1], helper(grid, i, j-1) + grid[i-1][j-1]);
        else if(i > 1)
            dp[i][j] = helper(grid, i-1, j) + grid[i-1][j-1];
        else if(j > 1)
            dp[i][j] = helper(grid, i, j-1) + grid[i-1][j-1];
        else dp[i][j] = grid[i-1][j-1];
        return dp[i][j];
    }

矩阵的总路径数

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

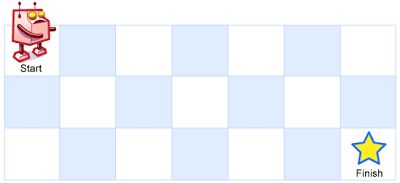
Above is a 7 x 3 grid. How many possible unique paths are there?

Note: m and n will be at most 100.

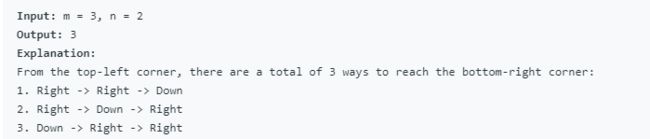
Example 1:

 

初看这道题感觉很简单，它不就是上面的点加左边的点的路径吗，但是小心，这是算一条路的，不能加上自己的，比如边界的整条边都算是一条路，所以只有不在边界的点的转向才可以算作是两条路径，这样的话可以写出代码如下

    private int[][] dp;
    private int uniquePaths(int m , int n){
        if(m == 0 || n == 0) return 0;
        if(m == 1 || n == 1) return 1;
        dp = new int[m+1][n+1];
        for (int i = 0 ; i <= m ; i++){
            Arrays.fill(dp[i], -1);
        }
        Arrays.fill(dp[0], 0);
        for(int i = 0 ; i <= m ; i++){
            dp[i][0] = 0;
        }
        for(int i = 1 ; i <= m ; i++){
            dp[i][1] = 1;
        }
        Arrays.fill(dp[1], 1);
        return helper(m, n);
    }
    private int helper(int m, int n){
        if(dp[m][n] != -1) return dp[m][n];
        /**
         * 边界检测
         */
        if(m > 1 && n > 1) dp[m][n] = helper(m-1, n) + helper(m, n-1);
        return dp[m][n];
    }

我是通过定义dp数组初始值的方式来排除边界点的，当然也可以通过其他的方式，反正只计算中间的店即可