1.本周学习总结
1.思维导图
2.谈谈你对图结构的认识及学习体会。
1.图在代码上相对于树来讲更好理解一点,因为图的操作没有像树那样子再频繁的接触递归了,但是图的问题需要考虑到很多算法,整体上算法难度也比较大。
2.掌握图,首先要掌握其存储方式,领接矩阵和邻接表的创建和使用的熟练很重要,我觉得在做题时,可以没有必要像课本那样子定义结构体来建领接矩阵,直接通过二维数组即可,但在未来很多大工程中则不适用,还是要规矩定义严格的结构体,可以为使用它而节省更多的时间等。
3.对于求最小生成树的算法,克鲁斯卡尔算法相对于prim算法来说更容易理解且时间复杂度更低,但在代码量上prim更为简洁;而对于最短路径问题来说,Dijkstra算法则有点类似prim算法,且较Floyd算法较为好理解些,实现上Floyd算法代码极简,但时间复杂度很高为O(n的三次方)。掌握这些算法对于学习图知识非常有必要。
4.再则拓扑排序,可以通过很多种方式实现,但要按要求做题,且要控制好入度的值;对于AOE网与关键路径则要了解其原理和实现,代码上不做需求。
5.学习本章内容对于链表操作也有了很大提升,以及在使用邻接矩阵过程中对多重结构体嵌套使用也有了一定理解和提升。2.PTA实验作业
2.1.题目1:7-1 图着色问题 (25 分)
2.1.1设计思路(伪代码)
- 整体思路:创建临边矩阵,将边信息存入后判断着色情况;先判断颜色数量是否满足要求,若不满足则直接输出no并退出函数;若满足,则再判断相邻两个顶点的颜色是否相同,若相同则直接输出no并退出循环。
这里主要介绍JudgeColor(MGraph g, int n, int colors)//判断着色是否正确
定义color整型数组用于存放顶点
将color数组中的数都初始化为-1
定义flag用于判断颜色是否计数重复
定义count用于计数颜色数量
for int i=1 to n do
输入color[i]
for int j=1 to i do j++
if color[i]=color[j] do //当颜色相同则不再进行计数
flag=0 break
end if
end for
if flag=1 do
count加一
end if
flag=1 //判断完一个颜色后,将flag重新赋值为1
end for
if count不等于colors do
输出no
return
end if
for i=1 to n do i++
for j=i+1 to n do j++
if 边存在且边所在两个点的颜色相同 do
输出no
return
end if
end for
end for
输出yes - 函数介绍
这里介绍一下memset函数
头文件:cstring
功能:给数组中的数赋初值
memset()函数原型是extern void *memset(void *buffer, int c, int count) buffer:为指针或是数组,c:是赋给buffer的值,count:是buffer的长度.2.1.2代码截图
2.1.3本题PTA提交列表说明。
- Q1:刚开始提交错误是最小k中颜色答案错误和最大图段错误;
- A1:先解决最小k种颜色问题,理解有误,以为count数大于colors才是错误的,所以写成下面的代码
 。条件修改成不等于要求的颜色数即可。
。条件修改成不等于要求的颜色数即可。 - A2:段错误的原因归结为数组超出范围,将数组最大值改大超过要求数组范围即可。
2.2.题目2:7-6 修建道路 (30 分)
2.2.1设计思路(伪代码)
- 整体思路:运用Kruskal算法找最小生成树的问题,对改算法改进即可,因为修建道路之前已经有几条路是已经建好的,在建树之前应将这些顶点的Vset值进行修改后再开始找最小生成树即可。
这里主要介绍主要功能函数Kruskal()
定义sum计算修建公路总长度
定义数组vset数组并将个数组值赋值其下标的值
定义Edge结构体类型的数组E
for i=0 to g.n do i++
for j=0 to i do j++
if g.edges[i][j]不等于零且不等于无穷 do
将起止顶点信息及该边长度依次赋值给E[k]
k++
end if
end for
end for
采用冒泡排序对E数组按权值升序排序
k=1 //k表示当前构造的生成树的第几条边,初值为1
输入n
while n-- do
输入已经连通的两个顶点的值
if 两个顶点为下标的vset数组值相等 do
再将集合中为sn2值的顶点集合编号都修改为sn1
k++
end if
end while
j=0
while k2.2.2代码截图
2.2.3本题PTA提交列表说明。
- Q1:答案错误显示段错误;
- A1:找数组超范围的情况,即数组不够大,以为村庄最多100个,所以最大值只要大于一百就好了;
- Q2:再次提交还有段错误;
- A2:发现结构体E中值是矩阵式一个一个存入的,则至少是n²的情况,所以调大最大情况为10000以上次才可以。
2.3.题目3:7-7 旅游规划 (25 分)
2.3.1设计思路(伪代码)
- 整体思路:运用Floyd算法求最短路径,在求最短路径的判断条件上加上路径相同且花费较少的判断条件即可;
介绍主功能函数Floyd()
for k=0 to n do k++
for i=0 to n do i++
for j=0 to n do j++
if 发现新的最短路径 or 发现一条路径与原路径长度相同且花费较少 do
//修改最短路径长度
//修改最低花费或最短路径花费
end if
end for
end for
end for
/*Floyd算法时间复杂度高,为O(n的三次方)*/2.3.2代码截图
2.3.3本题PTA提交列表说明。
- Q1: 刚开始按照课本上的思路写Floyd算法,并进行相应改进,但是运行出来的数据并实际正确数据大很多;
- A1:进行调试,发现在三重循环中的if判断句中,每次都会执行成功,所以怀疑那里有问题,由于if判断句很长导致检查起来非常费劲,所以看了好久都没有看出来有什么问题,后面终于发现是if后藏了一个;号,导致if语句一直执行的假象,修改后即可。
3、上机考试错题及处理办法
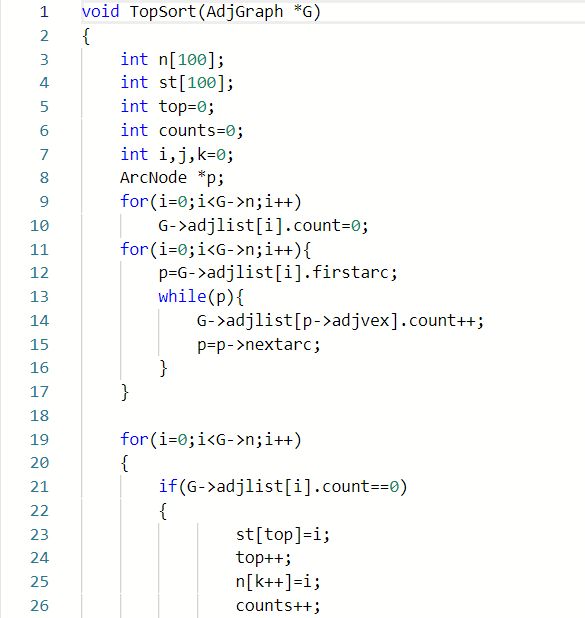
3.1.1 错题题目:6-3 jmu-ds-拓扑排序 (20 分)
3.1.2 错题代码:
3.1.3 修改后的代码:
3.1.4 错的原因及处理方法:
错误原因:因为本题为函数题,而头文件是确定的,所以无法使用stl库函数中的stack,导致得自己得通过数组设计栈,但在设计时没有控制好top的值,导致栈顶元素控制上可能有问题;
但在考试时又很难发现,且测试数据都可以通过,就是放上答案无法通过,导致在这题上花了大把时间,后面的题目都来不及写了,所以以后这种考试也好,平常做题也好,也不要太死
磕一题,真的得不偿失!
//分界线
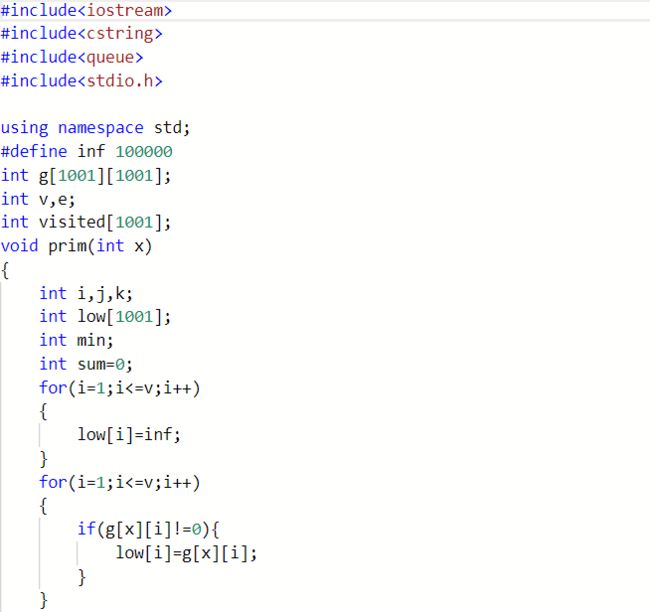
处理方法:修改top初值为-1,然后在入栈时改为++top,这样子使栈顶位置明确,便于取栈顶等操作。3.2.1 错题题目:7-2 公路村村通 (30 分)
3.2.2 错题代码:
3.2.3 修改后的代码:
3.2.4 错的原因及处理方法:
错误原因:对prim算法运用的不熟练,对其内的一些操作不是很理解,导致写代码时磕磕碰碰,难免遇到很多问题,但如果没有从本质上去理解算法的话,即使
是去调试,也无从判断错误在哪里。
//分界线
处理方法:重新复习课本上prim算法,再在自己试着去写代码和调试,从而完成对原先代码的修改。当遇到还有不懂的问题时,再翻书解决。3.3.1 错题题目:6-1 jmu-ds-最短路径 (20 分)
3.3.2 错题代码:此题没写,无错误代码。
3.3.3 修改后的代码:
3.3.4 错的原因及处理方法:
错误原因:因为之前写最短路径时用到的算法是Floyd算法,所以对Dijkstra算法没有太多的了解,在考试时看到这道题时就直接略过了。
//分割线
处理方法:看了书上的代码后,发现Dijkstra算法其实和Prim算法相似,在理解prim基础上再去理解Dikstra算法较为简单些。