字符串查找与匹配之KMP算法

一、字符串查找：
1、在Word、 IntelliJ IDEA、Codeblocks等编辑器中都有字符串查找功能。
2、字符串查找算法是一种搜索算法，目的是在一个长的字符串中找出是否包含某个子字符串。

二、字符串匹配：
1、一个字符串是一个定义在有限字母表上的字符序列。
例如，ATCTAGAGA是字母表 E ={A,C,G,T}上的一个字符串。
2、字符串匹配算法就是在一个大的字符串T中搜索某个字符串P的所有出现位置。
其中，T称为文本，P称为模式，T和P都定义在同一个字母表E上。
3、字符串匹配的应用包括信息检索、拼写检查、语言翻译、数据压缩、网络入侵检测。

三、字符串查找与匹配算法：
1、朴素查找算法(Naive string search algorithm)
2、KMP算法(Knuth-Morris- -Pratt algorithm)
3、BM算法(Boyer-Moore string search algorithm)

问题：
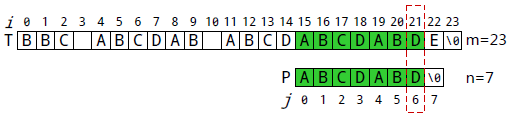
给定一个文本T字符串和一个模式P字符串， 查找P在T中的位置。
记号：
m、n：分别表示T和P的长度。
E：T和P的字符都定义在同一个字母集E上。
Ti、Pj： T的第i个字符和P的第j个字符(以0起始)。其中0≤i

(二)KMP算法：

1、算法原理：

KMP算法是一种高效的前缀匹配算法，在暴力匹配BF算法的基础上改进而来。
它利用之前已经部分匹配的有效信息，保持i不回溯，通过修改j的位置，
让模式串P尽量地移动到有效的位置，每次移动的距离可以不是1而是更大。

KMP算法的核心是计算模式串P每一个位置之前的字符串的前缀和后缀公共部分的最大长度
(不包括字符串本身，否则最大长度始终是字符串本身)。
获得P每一个位置的最大公共长度之后，就可以利用该最大公共长度快速和文本串T比较。
当每次比较到两个字符串的字符不同时，我们就可以根据最大公共长度将模式串P向前移动
(已匹配长度减去最大公共长度)位，接着继续比较下一个位置。模式串P的前移只是概念上的前移，
只要在比较的时候从最大公共长度之后比较P和T即可达到字符串P前移的目的。

2、next数组计算：

理解了KMP算法的基本原理，下一步就是要获得模式串P每一个位置的最大公共长度，
记为next数组。假设我们现在已经求得next[1]、next[2]、 ...next[i]，分别表示长度为1到i的
字符串的前缀和后缀最大公共长度，现在要求next[i+1]。

 

如果位置i和位置next[i]处的两个字符相同，则next[i+1]等于next[i]加1。如果两个位置的字符不相同，
就可以将长度为next[i]的字符串继续分割，获得其最大公共长度next[next[i]]，
然后再和位置i的字符比较。因为长度为next[i]前缀和后缀都可以分割成上部的构造，
如果位置next[next[i]和位置i的字符相同，则next[i+1]就等于next[next[i]]加1。
如果不相等，就可以继续分割长度为next[next[i]]的字符串，直到字符串长度为0为止。

3、求解方法：

假定当前匹配中，文本T匹配到i位置，模式P匹配到j位置，则：
①如果j!=-1，且当前字符匹配失败(即T[i]!=P[j]) ，令i不变，j=next[j]，
这意味着失配时，模式串P相对于文本串T向右移动了j-next[j]位;
②如果j=-1，或者当前字符匹配成功(即T[i]==P[j]) ，令i++，j++，继续匹配下一个字符。
③若j≥n，则包含P一次，匹配位置=i-j。

当匹配失败时，模式串P向右移动的位数为：失配字符所在位置减去失配字符对应的next值，
即移动的实际位数为： j - nextj]，且此值大于等于1。
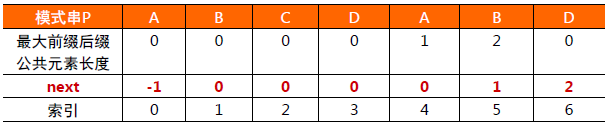
其中，next 数组各值的含义代表当前字符之前的字符串中，有多大长度的相同前缀后缀。

例如若next[j]=k， 代表j之前的字符串中有最大长度为k的相同前缀后缀。
这表示在某个字符失配时，该字符对应的next值会确定下一步匹配中，
模式串应该跳到哪个位置(跳到next[j]的位置)。如果next [j] 等于0或-1,则跳到模式串P的起始字符，
若next[j]= k且k> 0，代表下次匹配跳到j之前的某个字符,而不是跳到起始，且具体跳过了k个字符。

最长前缀后缀：
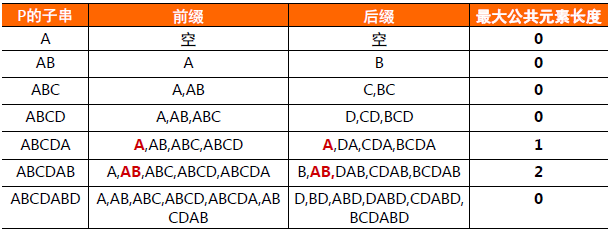
给定模式串P="ABCDABD"， 从左至右遍历整个P，其各个子串的前缀后缀分别如下表所示：

 

最大长度表：
模式串P子串对应的各个前缀后缀的公共元素最大长度表如下：

 

失配时，模式串P向右移动的位数为：(相减)
已匹配字符数 - 失配字符上一位字符所对应的最大长度值

当匹配到一个字符失配时，其实没必要考虑当前失配的字符，只看失配字符的
上一位字符对应的最大长度值。如此，便得出next数组。

 

next数组：寻找最大对称长度的前缀后缀，然后整体右移位，初值赋为-1。 

当失配时，模式串P向右移动的位数为：(相减)
失配字符所在位置 - 失配字符对应的next值

4、求解分析：

 

(1)开始时，i=0, j=0
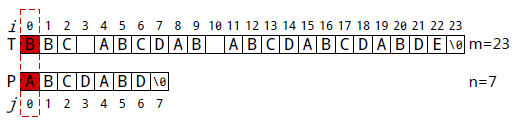
P[0]=A与T[0]=B失配。执行①：如果j!=-1， 且当前字符匹配失败(即T[i]!=P[j])，
令i不变，j=next[j]。 得到j=-1。转而执行②：如果j=-1，或者当前字符匹配成功
(即T[i]==P[j]) ，令i++, j++,得到i=1, j=0，即P[0]继续跟T[1]匹配。

 

(2)接下来，i=1, j=0
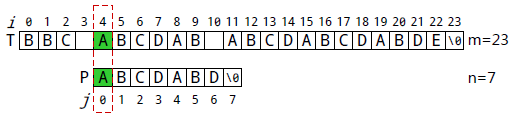
P[0]与T[1]失配。执行①： j=next[j]， j=-1。 执行②： i++, j++,得到i=2，j=0, 即P[0]继续跟T[2]匹配。

 

(3)接下来，i=4, j=0
P[0]与T[4]匹配。执行②： i++，j++，得到i=5，j=1。

 

(4)接下来，i=10, j=6
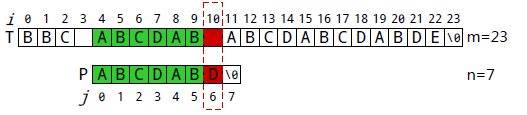
P[6]与T[10]失配。执行①：i不变， j=next[j]， 得到j=2。 所以下一步用P[2]
继续跟T[10]匹配，相当于P向右移动：j-next[j]=6-2=4位。

 

(5)接下来，i=10， j=2
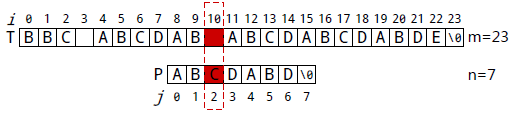
P[2]与T[10]失配。执行①：i不变，j=next[j]， 得到j=0。所以下一步用P[0]
继续跟T[10]匹配，相当于P向右移动: j-next[j]=2-0=2 位。

 

(6)接下来，i=10, j=0
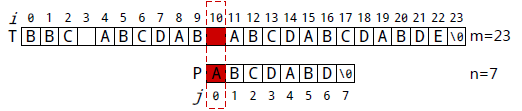
P[0]与T[10]失配。执行①: j=nextj]， j=-1。执行②: i++，j++,
得到i=11， j=0，即P[0]继续跟T[11]匹配。

 

(7)接下来，i=17，j=6
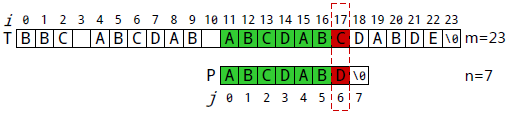
P[6]与T[17]失配。执行①: i 不变，j=next[j]， 得到j=2。 所以下一步用P[2]
继续跟T[10]匹配，相当于P向右移动: j-next[j]=6-2= 4位。

 

(8)接下来，i=17, j=2
P[2]与T[17]匹配。执行②： i++, j++，得到i=18, j=3。

 

(9)接下来，i=21，j=6
P[6]与T[21]匹配。执行②： i++, j++，得到i=21, j=7。
此时j≥n，执行③：T包含P一次，匹配位置=i-j=15。

算法性能：BF算法的时间复杂度是O(m*n)， KMP算法的时间复杂度是O(m+n)。

 1 #include
 2 #include<string.h>
 3 void preNext(char P[],int next[]){
 4     int m,k=-1,j=0;
 5     m=strlen(P);
 6     next[0]=-1;
 7     while(j1){
 8         //P[k]表示前缀，P[j]表示后缀
 9         if(k==-1||P[j]==P[k]){
10             ++j,++k;
11             if(P[j]!=P[k]) next[j]=k;
12             else next[j]=next[k];
13             //避免p[j]=p[next[j]]， 需要递归
14         }
15         else k=next[k];
16     }
17 }
18 
19 int KMP(char T[],char P[]){
20     int i=0,j=0,m,n;
21     int next[1000];
22     m=strlen(P);
23     n=strlen(T);
24     preNext(P,next);
25     while(im){
26         if(j==-1||T[i]==P[j]) i++,j++;
27         //如果j!=-1, 且当前字符匹配失败(即T[i]!=P[j]),
28         //令i不变，j=next[j]
29         else j=next[j];
30     }
31     if(j>=m) return i-j;
32     //匹配成功，返回P在T中第1次出现的位置
33     else return -1; //否则返回-1 
34 }
35 
36 int main(){
37     char T[]="ABC ABCDAB ABCDABCDABDE";
38     char P[]="ABCDABD";
39     printf("%s在%s",P,T);
40     if(KMP(T,P)>=0) printf("找到！");
41     return 0; 
42 }