剑指Offer对答如流系列 - 重建二叉树

面试题6：重建二叉树

题目描述：

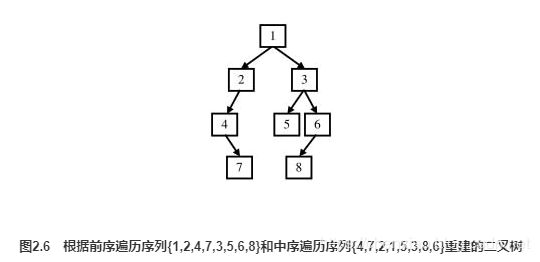
输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建出图2.6所示的二叉树并输出它的头结点。二叉树结点的定义如下：

class Node{
    int e;
    Node left;
    Node right;
    Node(int x) { e = x; }
}

这道题主要测试你对二叉树性质的了解，非常有代表性，不过在这之前，我们先把二叉树的基本性质捋一遍。

二叉树的基本性质

（1）关于树

树是一种数据结构，它是由n（n>=1）个有限结点组成一个具有层次关系的集合。

树的基本术语有：

• 每个结点有零个或多个子结点
• 没有父节点的结点称为根节点
• 每一个非根结点有且只有一个父节点
• 除了根结点外，每个子结点可以分为多个不相交的子树。
• 若一个结点有子树，那么该结点称为子树根的“双亲”，子树的根称为该结点的“孩子”。有相同双亲的结点互为“兄弟”。
• 一个结点的所有子树上的任何结点都是该结点的后裔。从根结点到某个结点的路径上的所有结点都是该结点的祖先。
• 结点的度：结点拥有的子树的数目
• 叶子结点：度为0的结点
• 分支结点：度不为0的结点
• 树的度：树中结点的最大的度
• 层次：根结点的层次为1，其余结点的层次等于该结点的双亲结点的层次加1
• 树的高度：树中结点的最大层次
• 森林：0个或多个不相交的树组成。对森林加上一个根，森林即成为树；删去根，树即成为森林。

“树”是计算机科学中非常重要的一部分内容，它的变形和应用非常之多。比如说，在做通讯录的时候，Android 工程师往往喜欢用字典树来存取数据，对于Java后端，有的时候我们处理的数据的时候也需要进行区间的查询，比如说去年你的博客在什么时间段关注你的人增长最快啊，一天中自己的博文阅读量最高的时间段啊，可以采用线段树来实现。在JDK1.8的HashMap的结构中，当元素超过8个的时候，会转为红黑树等等。

不过对于Java开发而言，二叉树是基础也是接触较多的一种结构。

（2）关于二叉树

二叉树是每个结点最多有两个子树的树结构。它有五种基本形态：

1)空树;

2)只有根的树,即单结点;

3)有根且有一个左子树;

4)有根且有一个右子树;

5)有根且有一个左子树,有一个右子树。

二叉树的性质有：

• 二叉树第i层上的结点数目最多为2i-1(i>=1)
• 深度为k的二叉树至多有2k-1个结点（k>=1）
• 包含n个结点的二叉树的高度至少为(log2n)+1

• 在任意一棵二叉树中，若叶子结点的个数为n0，度为2的结点数为n2，则n0=n2+1

  第四条的证明： 因为二叉树中所有结点的度数均不大于2，设n0表示度为0的结点个数，n1表示度为1的结点个数，n2表示度为2的结点个数。
  三类结点加起来为总结点个数，于是便可得到：n=n0+n1+n2 (公式1)
  由度之间的关系可得第二个等式：n=n0*0+n1*1+n2*2+1 即n=n1+2n2+1 (公式2)
  将（公式1）（公式2）组合在一起可得到n0=n2+1

了解这第四条性质就差不多了。如果想进一步学习二叉树的性质，不妨去找本《离散数学》？

对二叉树遍历的理解

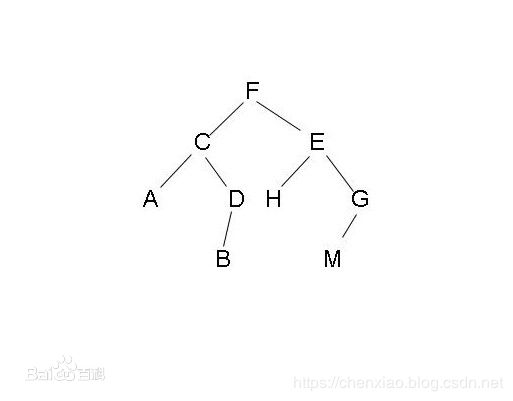
以这棵树为例：

前序遍历：根结点 —> 左子树 —> 右子树（先遍历根节点，然后左右）

    //前序遍历以node为根
    public void preOrder(Node node) {
        //终止条件
        if(node == null) {
            return;
        }
        System.out.println(node.e);
        preOrder(node.left);
        preOrder(node.right);
    }

这棵树的前序遍历为：FCADBEHGM

中序遍历：左子树—> 根结点 —> 右子树（在中间遍历根节点）

    //中序以node为根的
    public void inOrder(Node node) {
        //终止条件
        if(node == null) {
            return;
        }
        inOrder(node.left);
        System.out.println(node.e);
        inOrder(node.right);
    }

这棵树的中序遍历为：ACBDFHEMG

后序遍历：左子树 —> 右子树 —> 根结点（最后遍历根节点）

        //中序以node为根
        public void postOrder(Node node) {
            //终止条件
            if(node == null) {
                return;
            }
    
            postOrder(node.left);
            postOrder(node.right);
            System.out.println(node.e);
        }

这棵树的后序遍历为：ABDCHMGEF

层序遍历：

    //层序遍历
    public void levelOrder() {
        Queue q = new LinkedList<>();
        q.add(root);
        while( !q.isEmpty() ) {
            Node cur = q.remove();
            System.out.println(cur.e);
            
            if(cur.left != null)
                q.add(cur.left);
            if(cur.right != null)
                q.add(cur.right);  //后出
        }
    }

这棵树层序遍历为：FCEADHGBM

所谓的前序、中序、后序，就是对根节点而言的，左右的遍历顺序不变，前序就是根节点最先遍历，然后左右；中序就是把根节点放在中间遍历；后序则是把根节点放在最后遍历。

中序遍历能够帮助我们很好地确定根节点的位置，这个就有点可怕了，实际面试的时候，不单单会有给出前序遍历和中序遍历的结果让你重建二叉树，还有给出后序遍历和中序遍历结果或者 层序遍历和中序遍历的结果重建二叉树、

其他的遍历组合均不能还原出二叉树的形状，因为无法确认其左右孩子。例如，前序为AB，后序为AB，则无法确认出，B节点是A节点的左孩子还是右孩子，因此无法还原。

题解

思路：通过前序遍历获得根节点的位置，利用根节点将中序序列分为左子树和右子树，然后不断的递归划分即可。

代码中有解释。

  private Node buildTree(int[] pre, int preBegin, int preEnd, int[] mid, int midBegin, int midEnd) {
        // 前序遍历确第一个元素为根节点
        Node root = new Node(pre[preBegin]);
        // 用于标记中序遍历结果中根节点的位置
        int midRootLocation= 0;
        for (int i = midBegin; i <= midEnd; i++) {
            if (mid[i] == pre[preBegin]) {  
                midRootLocation= i;
                break;
            }
        }

        if ( midRootLocation - midBegin >= 1 ) {
            // 递归得到左子树
            
            // 中序遍历：左子树—> 根结点 —> 右子树（在中间遍历根节点）
            // midRootLocation标记了中序遍历结果中根节点的位置，这个位置两端对应根节点左子树和右子树
            // midRootLocation- midBegin 表示该根节点左边的节点的数量
            
            // 前序遍历：根结点 —> 左子树 —> 右子树（先遍历根节点，然后左右）
            // preBegin 标记了前序遍历结果中根节点的位置
            // preBegin + 1 表示该根节点左子树起始位置
            // preBegin + (midRootLocation- midBegin) 表示给根节点左子树结束的位置
            Node left = buildTree(pre, preBegin + 1, preBegin + (midRootLocation- midBegin),
                    mid, midBegin, midRootLocation - 1);
            root.left = left;
        }


        if ( midEnd - midRootLocation >= 1 ) {
            // 递归得到右子树
            // 原理和上面相同
            Node right = buildTree(pre, preEnd - (midEnd - midRootLocation) + 1, preEnd,
                    mid, midRootLocation+ 1, midEnd);
            root.right = right;
        }

        return root;
    }

举一反三

（1）给出后序遍历和中序遍历的结果重建二叉树

思路：通过后序获取根节点的位置，然后在中序中划分左子树和右子树，然后递归划分即可。

形式与上面 给出 前序遍历和中序遍历的结果重建二叉树相同

    private Node buildTree(int[] mid, int midBegin, int midEnd, int[] end, int endBegin, int endEnd) {
        
        Node root = new Node(end[endEnd]);
        int midRootLocation = 0;
        for (int i = midEnd; i >= midBegin; i--) {
            if (mid[i] == end[endEnd]) {
                midRootLocation = i;
                break;
            }
        }
        
        //还原左子树
        if (midRootLocation - midBegin >= 1 ) {
            Node left = buildTree(mid, midBegin, midRootLocation - 1, end, endBegin, endBegin + (midRootLocation - midBegin) - 1);
            root.left = left;
        }

        //还原右子树
        if (midEnd - midRootLocation >=  1 ) {
            Node right = buildTree(mid, midRootLocation + 1, midEnd, end, endEnd - (midEnd - midRootLocation), endEnd - 1);
            root.right = right;
        }
        
        return root;
    }

（2）给出层序遍历和中序遍历结果重建二叉树

思路：

（1）根据层序遍历获取根节点的位置

（2）根据（1）将中序划分为左子树和右子树

（3）根据（2）划分出的左子树和右子树分别在层序遍历中获取其对应的层序顺序

（4）然后递归调用划分。

  private Node buildTree(int[] mid, int[] level, int midBegin, int midEnd) {

        // 层序遍历的第一个结果是 根节点
        Node root = new Node(level[0]);
        // 用于标记中序遍历的根节点
        int midLocation = -1;
        for (int i = midBegin; i <= midEnd; i++) {
            if (mid[i] == level[0]) {
                midLocation = i;
                break;
            }
        }

        if (level.length >= 2) {
            if (isLeft(mid, level[0], level[1])) {
                Node left = buildTree(mid, getLevelArray(mid, midBegin, midLocation - 1, level), midBegin, midLocation - 1);
                root.left = left;
                if (level.length >= 3 && !isLeft(mid, level[0], level[2])) {
                    Node right = buildTree(mid, getLevelArray(mid, midLocation + 1, midEnd, level), midLocation + 1, midEnd);
                    root.right = right;
                }
            } else {
                Node right = buildTree(mid, getLevelArray(mid, midLocation + 1, midEnd, level), midLocation + 1, midEnd);
                root.right = right;
            }
        }
        return root;
    }


    // 功能 ： 判断元素是根节点的左子树节点还是右子树节点
    // 参数 ： target为根节点 isLeft在中序遍历结果中判断children是根节点的左子树还是右子树
    // 返回值 : 如果为左子树节点则为true 否则为false
    private boolean isLeft(int[] array, int target, int children) {
        boolean findC = false;

        for (int temp : array) {
            if (temp == children) {
                findC = true;
            } else if (temp == target) {
                return findC;
            }
        }
        return false;
    }


    // 功能： 将中序序列中midBegin与midEnd的元素依次从level中提取出来，保持level中的元素顺序不变
    private int[] getLevelArray(int[] mid, int midBegin, int midEnd, int[] level) {
        int[] result = new int[midEnd - midBegin + 1];
        int curLocation = 0;
        for (int i = 0; i < level.length; i++) {
            if (contains(mid, level[i], midBegin, midEnd)) {
                result[curLocation++] = level[i];
            }
        }
        return result;
    }

    // 如果array的begin和end位置之间（包括begin和end）含有target,则返回true。
    private boolean contains(int[] array, int target, int begin, int end) {
        for (int i = begin; i <= end; i++) {
            if (array[i] == target) {
                return true;
            }
        }
        return false;
    }