年底不忙, 还没放假,闲来无事刷数据库题玩玩.看到一个题,做完了觉得很有收获.也加深了对笛卡尔积的理解. 现记录在此
题目是力扣的, 叫做"分数排名"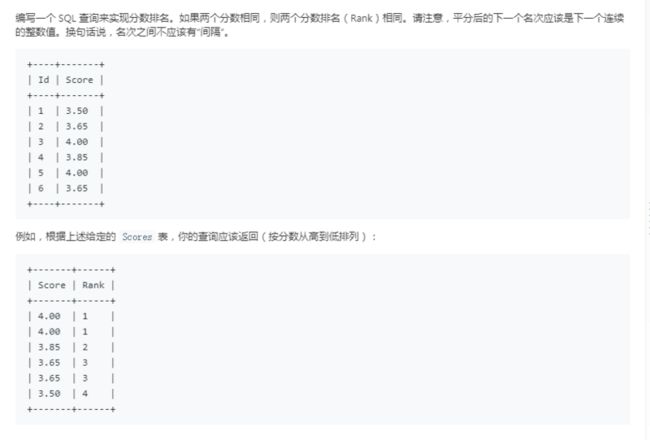
网上一个大牛的写法:
select s1.Score,count(distinct(s2.Score)) as Rank from
Scores s1,Scores s2
where
s1.Score <= s2.Score
group by s1.Id
order by Rank
数据库表连接数据行匹配时就会产生笛卡尔积,关于笛卡尔积的定义,引自百度百科:
笛卡尔乘积是指在数学中,两个集合_X_和_Y_的笛卡尔积(Cartesian product),又称直积,表示为_X_×_Y_,第一个对象是_X_的成员而第二个对象是_Y_的所有可能有序对的其中一个成员[3] 
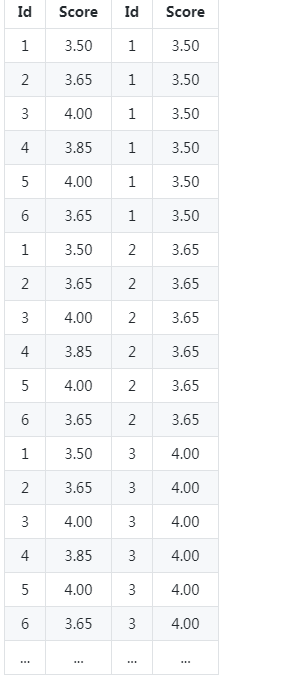
如果在数据库中进行表连接就会产生一个笛卡尔积临时表,在这个例子中如下:
查询第一条记录时: Id: 1 ,Score 3.50 当限定where s1.Score <= s2.Score时,结果集为:
{(3.50,3.50),(3.50,3.65),(3.50,4.00),(3.50,3.85),(3.50,4.00),(3.50,3.65)}
GROUP BY Id为1,即分出一条记录存在Id为1的数据集, 如果不加GROUP BY Id, 则会取所有结果集中最小的一条记录,而不是分组展示.
最后用distinct去重s2分数 剩下4个,取count,即 Rank为4
{(3.50,3.50),(3.50,3.65),(3.50,4.00),(3.50,3.85)}
第二条纪录: Id:2, Score: 3.65 当where s1.Score <= s2.Score时
{(3.65,3.65),(3.65,4.00),(3.65,3.85),(3.65,4.00),(3.65,3.65)}
{(3.65,3.65),(3.65,4.00),(3.65,3.85),(3.65,3.85),(3.65,3.65)}
GROUP BY Id为2, 分出一条记录存在Id为2的数据集
然后去重s2分数 剩下3个, 即Rank为3
{(3.65,3.65),(3.65,4.00)}
{(3.65,3.85)}
以此类推..
最后 order by Rank 按排名正序排列数据
如果把order by Rank去掉,得到下面结果集:
[[3.50, 4], [3.65, 3], [4.00, 1], [3.85, 2], [4.00, 1], [3.65, 3]]
每条数据内的分值默认是按照表的Id排列, 由此证明 上面分析的查询顺序没错