一、结点类与红黑树类:
(一)结点类基本数据成员:
1.左右子结点指针域
2.父结点指针域,方便回访父结点
3.有序 前驱 / 后继 指针域,迭代访问元素,提供一种顺序存储的假象
4.结点颜色,利用红黑规则,保持树的平衡。
(二)结点类的基本成员函数:
两个重载的构造函数,构造红色的新结点
(三)红黑树类基本数据成员:
1.头结点:保存一个据点,用来维系根节点与公用空结点
2.根结点:是红黑树的起始位置
3.空结点:作为所有空指针域的指向,一棵树只有一个
4.全局前驱、后继结点:用来使红黑树线索化,变得可迭代
(四)红黑树类基本成员函数(面向内部):
1.中序递归构造线索
2.结点左旋、右旋操作
3.插入后修正红黑树
4.移除后修正红黑树
5.移植(替换)结点
6.子树最大、最小结点
(五)红黑树类基本成员函数(面向用户):
1.构造函数,构造空树
2.空树判断
3.插入元素
4.移除元素
5.搜索元素
6.获取起始、终止迭代器、元素最大值、元素最小值
7.递归遍历
8.迭代器遍历
1 class RBTree; 2 enum Color{RED=0,BLACK=1}; 3 template4 class RBnode{ 5 friend class RBTree ; 6 public: 7 typedef RBnode * rb_iterator; 8 private: 9 typedef RBnode * Nodeptr; 10 public: 11 Nodeptr left,right,parent; 12 Nodeptr prior,next; 13 Color color; 14 public: 15 T val; 16 public://新结点都是红结点 17 RBnode(T value){left=right=parent=this;val=value;color=RED;} 18 RBnode(T value, Nodeptr l, Nodeptr r):val(value),left(l),right(r){parent=this,color=RED;} 19 }; 20 template 21 class RBTree{ 22 friend class RBnode ; 23 private: 24 typedef RBnode * Nodeptr; 25 public: 26 typedef RBnode * rb_iterator; 27 private: 28 Nodeptr header; 29 Nodeptr root; 30 Nodeptr nlnode; 31 Nodeptr _prior; 32 Nodeptr _next; 33 public: 34 RBTree(){ 35 header=new RBnode (0); 36 nlnode=new RBnode (-1); 37 nlnode->color = header->color = BLACK; 38 root=nlnode; 39 root->parent=header; 40 root->left=root->right=nlnode; 41 header->left=nlnode; 42 header->right=root; 43 nlnode->parent=nlnode; 44 header->next = nlnode; 45 header->prior = nlnode; 46 } 47 public: 48 bool isEmpyty(); 49 void Insert(T x); 50 void Insert(Nodeptr); 51 bool remove(T x); 52 bool remove(Nodeptr x); 53 Nodeptr search(T x); 54 T getMax(); 55 T getMin(); 56 rb_iterator begin(){return header->next;} 57 rb_iterator end(){return header;} 58 void inorderWalk(Nodeptr p) const ; 59 void LORvisit(); 60 void Iterator_visit(rb_iterator start, rb_iterator over) { 61 rb_iterator temp = start; 62 while(temp != over){ 63 cout << temp->val << ' '; 64 temp = temp->next; 65 } 66 } 67 private: 68 void LOR(); 69 void LOR(Nodeptr c); 70 void LeftRotate(Nodeptr x); 71 void RightRotate(Nodeptr x); 72 void Fix_up_insert(Nodeptr x); 73 void Fix_up_remove(Nodeptr x); 74 void Transplante(Nodeptr old, Nodeptr neo); 75 Nodeptr BranchMax(Nodeptr x); 76 Nodeptr BranchMin(Nodeptr x); 77 void LORvisit(Nodeptr c); 78 };
二、功能函数实现
(一)空树判断:
1 template2 bool RBTree ::isEmpyty(){ 3 return root == nlnode; 4 }
(二)插入结点:先把传入的元素进行封装,变成结点,再插入
templatevoid RBTree ::Insert(T x){ Nodeptr n=new RBnode (x, nlnode, nlnode); Insert(n); } template void RBTree ::Insert(Nodeptr x){ Nodeptr first,second; first = second = root; if(root == nlnode){ root = x; header->right = x; x->parent = header; x->color = BLACK; return; } while(first!=nlnode){ second = first; if(first->val > x->val){ first = first->left; }else if(first->val < x->val){ first = first->right; }else{ return ; } } x->parent = second; if(second->val > x->val){ second->left = x; }else{ second->right = x; } Fix_up_insert(x); LOR(); }
(三)左旋与右旋
1 template2 void RBTree ::LeftRotate(Nodeptr x){ 3 if(x->right == nlnode)//无右子树不可左旋,避免错误操作将树旋空 4 return; 5 Nodeptr x_r=x->right; 6 x->right = x_r->left; 7 if(x_r->left!=nlnode)//避免破坏空节点的特性:父结点指向自身 8 x_r->left->parent = x; 9 x_r->parent = x->parent; 10 if(x_r->parent == header){//根节点 11 root = x_r; 12 }else if(x->parent->left == x){//更新父结点 13 x->parent->left = x_r; 14 }else if(x->parent->right == x){ 15 x->parent->right = x_r; 16 } 17 x_r->left = x; 18 x->parent = x_r; 19 } 20 template 21 void RBTree ::RightRotate(Nodeptr x){ 22 if(x->left == nlnode)//无右子树不可左旋,避免错误操作将树旋空 23 return; 24 Nodeptr x_l=x->left; 25 x->left = x_l->right; 26 if(x_l->right!=nlnode)//避免破坏空节点的特性:父结点指向自身 27 x_l->right->parent = x; 28 x_l->parent = x->parent; 29 if(x_l->parent == header){//根节点 30 root = x_l; 31 }else if(x->parent->right == x){//更新父结点 32 x->parent->right = x_l; 33 }else if(x->parent->left == x){ 34 x->parent->left = x_l; 35 } 36 x_l->right = x; 37 x->parent = x_l; 38 }
(四)插入后修正
1 template2 void RBTree ::Fix_up_insert(Nodeptr x){ 3 while(x->parent->color==RED){//首先满足没有连续的红色结点 4 if(x->parent == x->parent->parent->left){ 5 if(x->parent->parent->right->color == RED){//case 1: son --red,dad&dad's brother --red 6 x->parent->parent->right->color = x->parent->color = BLACK; 7 x->parent->parent->color = RED; 8 x = x->parent->parent; 9 } 10 else{ 11 if(x == x->parent->right){//case 2:inner side,son --red,dad --red 12 x = x->parent; 13 LeftRotate(x); 14 } 15 x->parent->parent->color = RED;//case 3:outer side,son --red,dad --red 16 x->parent->color = BLACK; 17 x = x->parent; 18 RightRotate(x->parent->parent); 19 } 20 } 21 else{ 22 if(x->parent->parent->left->color == RED){//case 1: son --red,dad&dad's brother --red 23 x->parent->parent->left->color = x->parent->color = BLACK; 24 x->parent->parent->color = RED; 25 x = x->parent->parent; 26 } 27 else{ 28 if(x == x->parent->left){//case 2:inner side,son --red,dad --red 29 x = x->parent; 30 LeftRotate(x); 31 } 32 x->parent->parent->color = RED;//case 3:outer side,son --red,dad --red 33 x->parent->color = BLACK; 34 x = x->parent; 35 RightRotate(x->parent->parent); 36 } 37 } 38 } 39 root->color=BLACK; 40 }
(五)寻找元素:
1 template2 RBnode * RBTree ::search(T x){ 3 Nodeptr temp = root; 4 while(temp!=nlnode){ 5 if(temp->val > x){ 6 temp = temp->left; 7 }else if(temp->val < x){ 8 temp = temp->right; 9 }else{ 10 return temp; 11 } 12 } 13 return nlnode; 14 }
(六)移植(替换)结点:
1 template2 void RBTree ::Transplante(Nodeptr old, Nodeptr neo){ 3 if(old->parent == header){ 4 header->right = neo; 5 root = neo; 6 }else if(old->parent->left == old){ 7 old->parent->left = neo; 8 }else if(old->parent->right == old){ 9 old->parent->right = neo; 10 } 11 neo->parent = old->parent; 12 }
(七)子树最大最小结点:
1 template2 RBnode * RBTree ::BranchMax(Nodeptr x){ 3 if(x == nlnode) 4 return x; 5 Nodeptr temp=x; 6 while(temp->right!=nlnode){ 7 temp=temp->right; 8 } 9 return temp; 10 } 11 template 12 RBnode * RBTree ::BranchMin(Nodeptr x){ 13 if(x == nlnode) 14 return x; 15 Nodeptr temp=x; 16 while(temp->left!=nlnode){ 17 temp=temp->left; 18 } 19 return temp; 20 }
(八)移除结点:
1 template2 bool RBTree ::remove(T x){ 3 Nodeptr target = search(x); 4 if(target == nlnode){ 5 LOR(); 6 return false;} 7 return remove(target); 8 } 9 template 10 bool RBTree ::remove(Nodeptr x){ 11 Nodeptr a = x; 12 Nodeptr b = nlnode; 13 Color a_OriCo = a->color; 14 if(x->left==nlnode){//case 1:with one kid or no one 15 b = x->right; 16 Transplante(x, x->right); 17 }else if(x->right==nlnode){ 18 b = x->left; 19 Transplante(x, x->left); 20 }else{ 21 Nodeptr a=BranchMin(x->right); 22 a_OriCo = a->color; 23 b = a->right; 24 if(a->parent == x){//case 2:replace node is son of x 25 b->parent = a;//case nlnode 26 }else{ 27 Transplante(a, a->right);//a break away from there 28 a->right = x->right; 29 a->right->parent = a; 30 } 31 Transplante(x, a);//用新结点分支替换旧结点分支 32 a->left = x->left; 33 a->left->parent = a; 34 a->color = x->color; 35 } 36 delete x; 37 if(a_OriCo == BLACK){//case 3:违背红黑规则,路径黑结点数不同 38 Fix_up_remove(b); 39 } 40 LOR();//构建迭代联系,懒得写就直接从头构建了,这里应该仿造双链表删除结点来写 41 }
(九)删除后修正
1 template2 void RBTree ::Fix_up_remove(Nodeptr x){ 3 Nodeptr z = nlnode; 4 while(x!=root&&x->color==BLACK){ 5 if(x == x->parent->left){ 6 z=x->parent->right; 7 if(z->color == RED){//case 1:x's brather --red 8 z->color=BLACK; 9 x->parent->color = RED; 10 LeftRotate(x->parent);//利用红色来保持黑一致 11 z = x->parent->right;//update x's brother 12 }//case 2:x&x's brother sons color same 13 if(z->left->color==BLACK && z->right->color==BLACK){ 14 z->color = RED;//保持与x颜色一致,因为是兄弟结点 15 x = x->parent;//向上调整 16 } 17 else { 18 if(z->right->color==BLACK) {//z:x's brother 19 z->color = RED;//case 3:z left--red,right--black 20 z->left->color = BLACK; 21 RightRotate(z); 22 z = x->parent->right; 23 } 24 //case 4:adjust x and z 25 //将树平衡高度,保持了原父结点位置的颜色 26 z->color = x->parent->color; 27 x->parent->color = BLACK; 28 z->right->color = BLACK; 29 LeftRotate(x->parent); 30 break; 31 } 32 } 33 else { 34 z=x->parent->left; 35 if(z->color == RED){//case 1:x's brather --red 36 z->color=BLACK; 37 x->parent->color = RED; 38 this->RightRotate(x->parent);//利用红色来保持黑一致 39 z = x->parent->left;//update x's brother 40 }//case 2:x&x's brother sons color same 41 if(z->right->color==BLACK && z->left->color==BLACK){ 42 z->color = RED;//保持与x颜色一致,因为是兄弟结点 43 x = x->parent;//向上调整 44 } 45 else { 46 if(z->left->color==BLACK) {//z:x's brother 47 z->color = RED;//case 3:z left--red,right--black 48 z->right->color = BLACK; 49 LeftRotate(z); 50 z = x->parent->left; 51 } 52 //case 4:adjust x and z 53 //将树平衡高度,保持了原父结点位置的颜色 54 z->color = x->parent->color; 55 x->parent->color = BLACK; 56 z->left->color = BLACK; 57 RightRotate(x->parent); 58 break; 59 } 60 } 61 } 62 root->color = BLACK;//保持根为黑 63 }
(十)获取最大最小元素:
1 template2 T RBTree ::getMax(){ 3 return header->prior->val; 4 } 5 template 6 T RBTree ::getMin(){ 7 return header->next->val; 8 }
(十一)迭代构造线索
1 template2 void RBTree ::LOR(){ 3 _prior = _next = header; 4 LOR(root); 5 _next->next=header; 6 header->prior=_next; 7 } 8 template 9 void RBTree ::LOR(Nodeptr c){ 10 if(c->left != nlnode){ 11 LOR(c->left); 12 } 13 _prior = _next; 14 _next = c; 15 _prior->next=_next; 16 _next->prior=_prior; 17 if(c->right != nlnode){ 18 LOR(c->right); 19 } 20 }
(十二)递归遍历与迭代遍历:
1 template2 void RBTree ::LORvisit(){ 3 LORvisit(root); 4 cout << endl; 5 } 6 template 7 void RBTree ::LORvisit(Nodeptr c){ 8 if(c->left != nlnode){ 9 LORvisit(c->left); 10 } 11 cout << c->val << ' '; 12 if(c->right != nlnode){ 13 LORvisit(c->right); 14 } 15 } 16 void Iterator_visit(rb_iterator start, rb_iterator over) { 17 rb_iterator temp = start; 18 while(temp != over){ 19 cout << temp->val << ' '; 20 temp = temp->next; 21 } 22 }
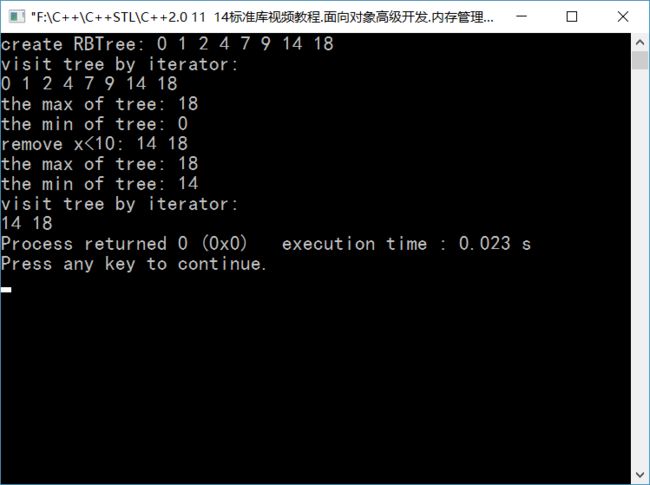
三、红黑树测试:
1 #include2 #include 3 #include "templateRBTree.h" 4 using namespace std; 5 6 int main() 7 { 8 RBTree<int> rb; 9 for(int i=0;i < 10;++i) 10 rb.Insert(rand()%20); 11 cout << "create RBTree: "; 12 rb.LORvisit(); 13 RBTree<int>::rb_iterator itr=rb.begin(); 14 cout << "visit tree by iterator: " << endl; 15 rb.Iterator_visit(itr, rb.end()); 16 cout << endl; 17 cout << "the max of tree: " << rb.getMax() << endl; 18 cout << "the min of tree: " << rb.getMin() << endl; 19 for(int i=0;i<10;++i) 20 rb.remove(i); 21 cout << "remove x<10: "; 22 rb.LORvisit(); 23 cout << "the max of tree: " << rb.getMax() << endl; 24 cout << "the min of tree: " << rb.getMin() << endl; 25 itr=rb.begin(); 26 cout << "visit tree by iterator: " << endl; 27 rb.Iterator_visit(itr, rb.end()); 28 return 0; 29 }