1、相关性比较??根据数据类型!!
数值数据与数值数据----相关系数
数值数据与分类数据----相关比
分类数据与分类数据----克莱姆相关系数---独立性检验(卡方检验)--根据教材画表格求卡方值,然后根据独立性检验,作出检验假设证明是否具有相关性。2、数据有两大类:连续变量(正态或非正态)、分类变量(二分类或多分类) 。 连续变量 中,正态与非正态数据表示方法是不一样的。 正态数据一般用均数土标准差(x±s) 方式表示,其数据95.45%处于x±s 范闱内;非正态数据用中位数和四分位间距表示;分类变量表示方法更直接 , 通常为频率与百分数。
3、比较单个结局和单个变量:临床中最常见的情况就是比较两种处理或手术的结果有何差异 。 如比较两组独立的结果,正态分布应选用t检验;连续非正态分布选用Mann-Whitney或Wilcoxon秩和检验;分类变量选用卡方检验,当数据量很小时,应用Fisher检验。
4、p为0.05的意义是 : 若不断重复检验,差异由偶然导致的概率为5%。
5、趋势检验:比较单个结局和多个变量:很多情况下 , 结局受多个变量影响,回归分析适用于这种情况。
其中包括线性(liner)回归,可应用 于连续正态分布的结局,如血钾 。二分类结局可应用逻辑(logistic)回归,其分析结果用比值比表示,即事件发生的比值与不发生比值的比值。 比值比常被误解为相对风险。同样需要对不同的结局类型采用相应的回归分析。一个常犯的错误是将连续变量转为二分类,本应使用线性回归,最后使用了logistic回归 。
以上均是一种结局(单个或多个自变)情况,没有考虑时间或丢失数据的因素,不能用于生存分析。 对于生存分析,应用Cox比例风险回归 。 计算得出风险比,表示死亡的相对风险 。
等级资料 用spearman相关性分析 (见下表)
参数分析结果的解读与此类似 , 只不过多了个 " F test to compare varian ces" , 即方差是否齐 。一 般认为, p值 > 0.10才可以认为两组数据方差 相同(注意 : 是大于 , 不是小于 ! 是0. 10 , 不是0.05 ! ) 。
如何判断数据是否成正态分布?
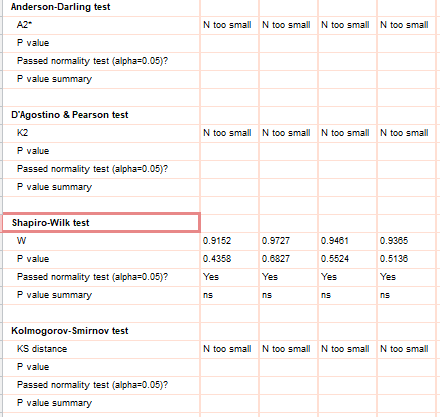
GraphPad Prism提供了3种检验数据是否呈正态分布的方法:D'Agootino-Pearson法, Kolmogorov-Smirnov法和Shapiro-Wilk法 。 针对同 一种数据, 3种方法的计算结果大同小异 。 虽然GraphPad Prism不推荐用 KolmogorovSmirnov 法,但根据笔者经验,在国际上发表论文时,多采用 KolmogorovSmirnov法的结果,可能是因为当样本 最 太小时, Shapiro-Wilk法和 D'AgootinoPearson法无法给出检验结果 。 当然 , 也可以 3种方法都选择,综合判断数据是否呈正态分布。具体在Column statistics下拉菜单中normality and lognormality tests(正态或对数正态分布)。选择好统计方法之后点击 "OK", 就可以得到正态检验的结果,如图 10所示。 需要特别说明的是 : 在正态检验中,一般认为p>0.10才表示数据呈正态分布(是大于,不是小于!是0.10, 不是0.05!)。
绘制生存曲线:
进入上述界面后点击选中左侧 "Survival" 模式,之后点击 "Create" , 之后进入了GraphPad Prism的主界面。GraphPad Prism 主界面的第一个纵列(标志了 X 的纵列)是用来输入随访时间的,其余纵列则输入患者的结局.每一个纵列代表了 一个组。输入数据如下图:
图像自动生成。
t检验
t检验有 三 种类型 : 独立样本 t检验、配对样本 t检验和单样本 t检验。若实验组和对照组未进行配对,在符合独立样本t检验使用条件的情况下 , 可采用独立样本t检验比较两组数据的差异是否具有统计学意义 ; 若实验组和对照组进行配对 , 在符合配对样本t检验使用条件的情况下,则应该使用配对t检验。
独立样本 t检验对数据的基本要求是:1.数据呈正态分布 2.总体方差相等。 配对样本的t检验则要求两组数据的差值呈正态分布 。
数据是否符合正态分布? 可以采用Kolmogorov-Smirnov检验或ShapiroWilk检验.在R中可以使用ks.test()函数。
(1)若数据呈正态分布,若方差整齐,则建议作者采用独立样本t检验的结果;但方差不整齐,则可以采用近似t检验对数据进行分析。 SPSS软件在进行t检验时,会自动计算方差齐性检验的结果,并同时告知t检验和近似t检验的统计学结果。(2)大多数医学数据都不呈正态分布 ,如血脂、血糖、肝酶、肿瘤标志物等.因此不宜使用 t检验进行两组数据的比较 , 而应该采用非参数统计方法,如Mann-Whitney检验 。
若实验设计有多个组,即同一实验因素下有多个分组 , 则不宜反复采用t检验进行组间比较。而应该采用单因素方差分析或K.ruskal-Wallis H检验,先从总体上明确几组之间的差异是否有统计学意义,然后根据研究需要决定是否进行两组间的比较,采用何种方法进行比较。
卡方检验
主要用于对分类资料进行比较分析。
处理四格表数据是卡方检验最为常见的用途之一。其目的在于分析”构成比”或者”率”之间的差异是否具有统计学意义。
1、对于四格表数据,使用卡方检验的条件:样本量>40 、且最小理论频数应>5。
2、对于某些小样本的、或者指标阳性率较低的研究,总样本量可能<40, 最小理论频数也可能<5, 此时应该采用Fisher确切概率法进行分析.
3、对于等级资料,秩转换之后进行Mann-Whitney U检验。
4、对于画表问题,不变的在左侧,变化的在上边,具体见下边表格的例子。
总结:分类资料用卡方,等级资料用秩和.
实际上,从理论上讲 , 若要分析四格表数据中的构成比或者率之间的差异是否有统计学意义, Fisher确切概率法的结果是最可靠的。 若是使用软件对数据进行分析,不论样本量和最小理论频数,均可采用Fisher确切概率法。
卡方检验回答的问题仅仅是"构成比”或者"率”之间的差异是否具有统计学意义 , 而不能回答效应指标的强度高低问题。
对于等级资料,不是率和构成比的问题,而是分期等问题,所以处理此类数据的一般方法是将分期进行秩转换 , 然后以秩和检验(MannWhitney 检验)进行统计分析 。
多组资料比较:在制作表格时,应遵循的原则是:分组因素(自变量)作为横标目,效应员(应变拭)作为纵标 目 。 分类资料用卡方,等级资料用秩和。
这是一个率的比较问题 , 研究目的主要是分析各种血型的人群HBV感染的发病率是否相同?处理此类数据,一般是直接采用卡方检验从整体上分析各组人群率(构成比)的差异是否具有统计学意义;若具有统计学意义 , 则根据研究目的决定是否进行组间的比较。 以本研究为例,研究者可能还需要逐一比较各组HBV感染的发病率之间的差异是否具有统计学意义。 处理此类数据时,最容易犯的一类错误就是将表格进行拆分成六个四格表反复采用卡方检验进行统计分析。 实际上.这种错误类似于“反复使用t检验比较多组资料”,会增大 l类误差的概率。 正确的做法:应该是采用卡方分割法,通过校正检验水准的方式来进行两两比较。
2行或2列以上计数资料的处理原则:
在本研究中,性别是在出生时就已决定的,而胰腺癌的TNM分期是在后天发生的 。 所以研究目的只能是阐述性别是否影响首诊胰腺癌患者TNM分析,而不是首诊TNM分期是否会影响性别(这个问题听起来也太滑稽了)。 所以,性别因素是分组因素(自变量), 是表格的"横标目", TNM分期是效应显(应变量) , 是表格的"纵标目"。
对于本组数据 , 有两种统计学方法可供选择,卡方检验和秩和检验(经过秩转换以后采用Mann-Whitney U检验比较),但两种方法的统计学结论和专业结论各不相同,甚至大相径庭。 若将TNM分期视为分类资料,即各个TNM分期之间无“高低强弱”之分,则可以采用卡方检验。 当p<0.05时,对应的统计学结论是男性和女性患者胰腺癌TNM分期的分布频数(或者说结构组成)不同。 若将TNM分期视为 等级资料 , 即 IV期患者较 I期严重,则采用秩和检验,即将所有数据进行秩转换后采用Mann-Whitney U检验进行统计分析。 假定男性的总秩次高于女性,当p<0.05时,对应的统计学结论是 : 男性患者的首诊TNM分期较女性患者高,即男性患者的肿瘤分期较女性严重;而对应的专业结论是:性别是影响TNM分期早晚的因素,或者说性别与TNM分期早晚有关。
某研究者发现基因A在胰腺癌组织 中 的表达异常 , 因此想研究胰腺癌的TNM分期是否是影响基因 A表达的因素 。 基因A的表达可以用“阳性 ” 和“阴性 ” 来表示 。 研究者调查了 226例胰腺癌患者 , 其中 108例患者A基因表达阳性 , 118例患者A基因表达阴性。该表格在排列方式上与表 1不同,分组因素是TNM分期 , 效应量是A基因的表达情况。 之所以这样排版 , 主要是因为本研究重点是要明确TNM分期是否会影响基因A的表达 , 而非A基因的表达是否会影响TNM分期。
直接采用卡方检验进行分析,若p<0.05, 得出的统计学结论是 : 不同TNM分期患者A基因表达状况的频数分布(distribution)之间的差异有统计学意义; 对应的专业结论是 : TNM分期可能影响胰腺癌患者中氏基因的表达特征(阳性还是阴性)。至于怎么影响 ? 升高还是降低?卡方检验无法回答
若将表格进行调整,得出表3, 再进行卡方检验,若p<0.05 , 对应的统计学结论是不同TNM分期患者A基因表达的阳性率(positive rate)之间的差异有统计学意义。对应的专业结论:胰腺癌的TNM分期可能会影响A基因表达的阳性率,然后根据阳性率大致排一个顺序:A基因在TNM分期胰腺癌患者中表达由高到低分别是:IV期>I期>II期>III期。若作者感兴趣,还可用卡方分割法对各组数据之间进行比较,观察组间是否具有统计学意义。
回到表3, 若要明确表达强度高低的问题 , 需要对数据进行秩转化,然后再采用Kruskal-Wallis H检验比较各个TNM分期患者基因表达强度的差异。 这里TNM分期可视为“分类变量" 。从专业上来讲,将A基因的表达情况进行秩转换之后再比较不同TNM分期患者之间A基因的表达情况 , 显然信息量更为丰富 , 更符合研究目的 。 但是考虑到当人们用“阳/阴性”去衡量A基因表达时,已经极大地降低了统计效率,损失了很多统计信息 , 这样统计出来的结果很有可能不可靠,所以一般通过阳性率从侧面反映基因的表达强度 。 笔者认为:卡方检验和秩和检验均可用于此类数据的分析,只是在下专业结论时需要注意区分"率”和“水平”的问题。
若将基因A的表达强度视为分类资料,直接采用卡方检验,若p<0.05, 对应的统计学结论为不同TNM分期患者A基因表达状况的频数分布(distribution)之间的差异有统计学意义 ; 对应的专业结论为TNM分期可能影响基因A的表达频数分布状况。 至于怎么影响,升高还是降低,卡方检验无法回答。若将基因的表达情况(高中低)视为有序变撮 , 则需要对其进行秩转换,之后再采用Kruskal-Wallis H检验进行比较,若p<0.05, 对应的统计学结论是不同TNM分期患者A基因表达强度之间的差异有统计学意义;对应的专业结论是TNM分期可能影响基因A的表达强度 。进一步根据各组的总秩次,可以明确各个TNM分期中基因A的表达强度,并根据需要判断是否有必要进行两两比较。
但是秩和检验还不是最佳选择 ! 在本研究中,我们注意到 : TNM分期和基因的表达强度都是“有序变侃" , 或者说都是”等级资料",如果能明确二者是否呈线性相关关系,显然更符合研究的目的 。 因此本研究最恰当的统计学方法应该是线性趋势检验或者Spearman秩相关法。
ROC曲线
ROC 曲线的纵坐标表示诊断敏感性; 横坐标通常为1 -特异性。在图1中,横坐标之所以为特异性是因为横坐标的刻度是从右向左读取的。实际上,如果横坐标的刻度是从左向右读取的话, 就应该标志为1 -特异性。1 -特异性其实就是表示误诊率,因此曲线走形越靠近左侧,表示待评价试验的误诊率越低,即诊断特异性越高。
1、曲线下面积越大,总体诊断效率越高。
2、总体样本量和疾病分布状况影响曲线的光滑程度。
3、曲线下面积(AUC)为1 时,表示检查手段有近乎完美的诊断价值; AUC 为0.5时,表示曲线没有任何诊断价值。
4、目前国际上一部分学者认为AUC介于0 .5 和0 .7之间表示检查手段的诊断效率较低;若AUC介于0.7和0 .9之间, 则表明检查手段具有中等诊断效率; 若AUC 大于0.9则表明检查手段具有较高的诊断效率。