本文内容主要参考《集体智慧编程》和遗传编程。遗传编程非常详细,极力推荐。
遗传编程是收到生物进化理论的启发而形成的一种机器学习技术。其通常的工作方式是:以一大堆程序(称为种群)开始——这些程序可以是随机产生的,也可以是人为设计的,并且它们被认为是在某种程度上的一组最优解。随后,这些程序将会在一个由用户定义的任务中展开竞争。此处所谓的任务或许是一种竞赛,各个程序在竞赛中彼此直接展开竞争,或者也有可能是一种个体测试,其目的是要测出那个程序的执行效果更好。待竞争结束后,我们会得到一个针对所有程序的评价列表,该列表按程序的表现成绩从最好到最差顺次排序。
接下来——也正是进化得以体现的地方——算法可以采取两种不同的方式对表现最好的程序实施复制和修改。比较简单的一种方式称为变异(mutation),算法会对程序的某些部分以随机的方式稍作修改,希望借此能够产生一个更好地解来。另一种修改程序的方式称为交叉,也称为配对(基因重组),其做法是:先将某个最优程序的一部分去掉,然后再选择其他最优程序的一部分来代替之。这样的复制和修改过程会产生许多新的程序来,这些程序基于原来的最优程序,但又不同于他们。
在每一个复制和修改的阶段,算法都会借助于一个适当的函数对程序的质量作出评估。因为种群的大小始终是保持不变的,所以许多表现极差的程序都会从种群中被剔除出去,从而为新的程序腾出空间。新的种群被称“下一代”,而整个过程则会一直不断地重复下去,因为最优秀的程序一直被保留了下来,而且算法又是在此基础上进行复制和修改的,所以我们有理由相信,每一代的表现都会比前一代更加出色;这在很大程度上有点类似与人类世界中,年轻一代比他们的父辈更聪明。
创建新一代的过程直到终止条件满足才会结束,具体问题不同,可能的终止条件也不同。
- 找到了最优解
- 找到了表现足够好的解
- 题解在历经数代之后都没有得到任何改善
- 繁衍的代数达到了规定的限制
基于树的遗传编程
为了构造出能够用以测试、变异和配对的程序,我们需要一种能够在Python代码中描述和运行这些程序的方法。基于树的遗传编程是遗传编程最早的形态,也是遗传编程的主流方法。
大多数编程语言,在变异或解释时,首先都会被转换成一颗解析树,这棵树非常类似于我们将要用到的树。
树上的节点可能是枝节点也可能是叶节点:
- 枝节点代表了应用于其子节点上的某一种操作;
- 叶节点表示一个输入的参数或者变量。
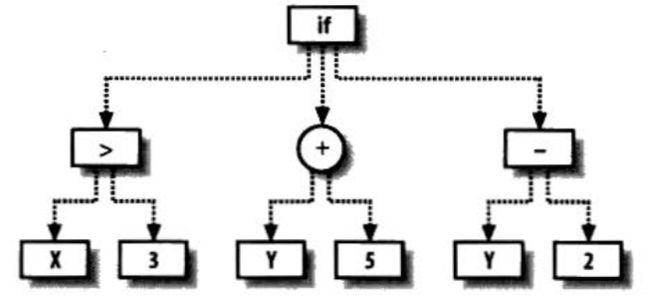
如上所示的树可用下面的代码进行表示:
def func(x, y):
if x>3:
return y+5
else:
return y-2
在Python中表现树
在本节我们介绍下如何在Python中构造树状程序。这棵树是由若干节点组成的:
- 函数节点:根据与之关联的函数的不同,这些节点又可以拥有一定数量的子节点;
- 参数节点:这些节点将会返回传递给程序的参数;
- 常数节点:这些节点则会返回常量;
那些最值得关注的节点则会返回应用于其子节点之上的操作。
from random import random, randint, choice
from copy import deepcopy
from math import log
class Fwrapper(object):
'''封装类,对应于"函数型"节点上的函数。其成员变量包括了函数名称、函数本身、
以及该函数接受的参数个数
'''
def __init__(self, function, childcount, name):
self.function = function
self.childcount = childcount
self.name = name
class Node(object):
'''对应于函数型节点(即带子节点的节点)。我们以一个Fwrapper类对其进行初始化。
当evaluate被调用时,我们会对各个子节点进行求值运算,然后再将函数本身应用于求得的结果。
'''
def __init__(self, fw, children):
self.function = fw.function
self.name = fw.name
self.children = children
def evaluate(self, inp):
'''
'''
results = [n.evaluate(inp) for n in self.children]
return self.function(results)
def display(self, indent=0):
'''
'''
print((' '*indent)+self.name)
for c in self.children:
c.display(indent+1)
class ParamNode(object):
'''这个类对应的节点只返回传递给程序的某个参数。
其evaluate方法返回的是由idx指定的参数
'''
def __init__(self, idx):
self.idx = idx
def evaluate(self, inp):
return inp[self.idx]
def display(self, indent=0):
'''打印该节点返回参数的对应索引
'''
print(('%sp%d'%(' '*indent, self.idx)))
class ConstNode(object):
'''返回常量值的节点。其evaluate方法返回该类被初始化时所传入的值
'''
def __init__(self, v):
self.v = v
def evaluate(self, inp):
'''
'''
return self.v
def display(self, indent=0):
'''
'''
print('%s%d'%(' '*indent, self.v))
# 一些针对节点操作的函数
addw = Fwrapper(lambda l: l[0]+l[1], 2, 'add')
subw = Fwrapper(lambda l: l[0]-l[1], 2, 'subtract')
mulw = Fwrapper(lambda l: l[0]*l[1], 2, 'multiply')
def if_func(l):
'''条件运算函数
'''
if l[0]>0:
return l[1]
else:
return l[2]
ifw = Fwrapper(if_func, 3, 'if')
def is_greater(l):
if l[0]>l[1]:
return 1
return 0
gtw = Fwrapper(is_greater, 2, 'is_greater')
flist = [addw, subw, mulw, ifw, gtw, subw]
下面来测试一下我们的树:
def example_tree():
'''
'''
return Node(ifw, [Node(gtw, [ParamNode(0), ConstNode(3)]),
Node(addw, [ParamNode(1), ConstNode(5)]),
Node(subw, [ParamNode(1), ConstNode(2)])])
example_tree().evaluate([5,3])
# 输出
8
example_tree().display()
# 输出
example_tree().display()
1
example_tree().display()
if
is_greater
p0
3
add
p1
5
subtract
p1
2
构造初始种群
通常初始种群是由一组随机程序构成的,这样做可以在初始种群中引入更加丰富的多样性,具有更广泛的适应性。虽然我们可以针对某个问题去专门设计相应的程序来获得可能正确的答案,但是这些答案很可能与我们最终的结果截然不同。
创建一个随机程序的步骤包括:创建根节点并为其随机指定一个关联函数,然后在随机创建尽可能多的子节点;相应地,这些子节点也可能会有他们自己的随机关联子节点。和大多数对树进行操作的函数一样,这一过程很容易以递归的形式进行定义。
def make_random_tree(pc, max_deepth=4, fpr=0.5, ppr=0.6):
'''随机生成程序树
Args:
pc: 程序树所需输入参数的个数
max_deepth: 限制树的深度,防止栈溢出
fpr: 新建节点属于函数型节点的概率
ppr: 新建节点不是函数节点而是参数节点(paramnode)的概率
'''
if random() < fpr and max_deepth > 0:
f = choice(flist)
children = [make_random_tree(pc, max_deepth-1, fpr, ppr)
for i in range(f.childcount)]
return Node(f, children)
elif random() < ppr:
return ParamNode(randint(0, pc-1))
else:
return ConstNode(randint(0, 10))
对程序进行变异(突变)
当表现最好的程序被选定之后,他们就会被复制并修改以进入到下一代。如本文一开始所说,变异能够使得我们这些最好的程序得以进化。而变异的做法就是对某个程序进行少许的修改。一个树状程序的修改(变异)方式有多种:
- 可以改变节点上的函数;
- 可以改变节点的分支;
- 也可以增加或删除分支;
- 此外,还可以用一棵全新的树来替换某一子树。
最后,变异的次数不宜过多。
def mutate(t, pc, prob_change=0.1):
'''替换子树
'''
if random() < prob_change:
return make_random_tree(pc)
else:
result = deepcopy(t)
if isinstance(t, Node):
# 递归的测试所有level层的树节点是否需要变异
result.children = [mutate(c, pc, prob_change) for c in t.children]
return result
random2 = make_random_tree(2)
random2.display()
# 输出
add
subtract
p1
p1
p0
muttree = mutate(random2, 2)
muttree.display()
# 输出
add
subtract
p1
p1
5
交叉变异
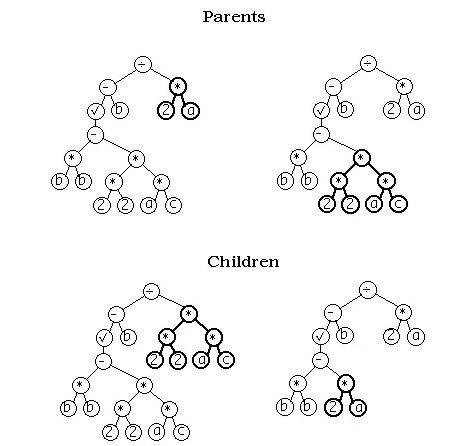
除了突变外,另一种修改程序的方法称为交叉或配对,其做法是:从众多程序中选出两个表现优异者,并将其组合在一起构造出一个新的程序,通常的组合方式是用一棵树的分支取代另一棵树的分支。
def crossover(t1, t2, prob_swap=0.7, top=1):
'''交叉变异以两棵树作为输入,并同时开始向下遍历。当达到某个选定的阈值时,函数
便会返回前一棵树的一份拷贝,树上的某个分支会被后一棵树上的一个分支所取代。通过
对两棵树的即时遍历,函数会在每棵树上大致位于相同层次的节点处实施交叉操作。
'''
if random()衡量程序优劣
有了生成程序的方法还不够,我们还需要一个方法来衡量各种程序的优劣以挑选优秀个体使得种群得以进化。
def score_function(tree, s):
'''衡量题解优劣的函数,相当于损失函数
'''
dif = 0
for data in s:
v = tree.evaluate([data[0], data[1]])
dif+=abs(v-data[2])
return dif
构筑环境
有了衡量程序优劣的办法和修改程序的办法,现在可以开始构筑供程序进化用的竞争环境了。
def evolve(pc, popsize, rank_function, max_gen=500,mutation_rate=0.1,
breeding_rate=0.4, pexp=0.7, pnew=0.05):
'''种群迭代进化以找到
Args:
pc: 程序树所需输入参数的个数
popsize: 初始种群的大小
rank_function: 将一组程序按从优到劣的顺序进行排序的函数
max_gen: 最大繁殖(迭代)次数
mutation_rate: 代表了发生变异的概率,该参数会被传递给mutate
breeding_rate: 代表了发生交叉的概率,该参数会被传递给crossover
pexp: 表示在构造新的种群时,"选择评价比较低的程序"这一概率的递减比率。
该值越大,相应的筛选过程就越严格,即:只选择评价最高者作为复制对象
的概率就越大
pnew: 表示在构造新种群时,"引入一个全新的随机程序的概率"
'''
# 返回一个随机数,通常是一个较小的数
# pexp的取值越小,我们得到的随机数就越小
def select_index():
return int(log(random())/log(pexp))
# 创建一个随机的初始种群
population = [make_random_tree(pc) for i in range(popsize)]
for i in range(max_gen):
scores = rank_function(population)
print(scores[0][0])
if scores[0][0]==0:
break
# 总能得到两个最优的程序
new_pop = [scores[0][1], scores[1][1]]
# 构造下一代
while len(new_pop)pnew:
new_pop.append(mutate(
crossover(scores[select_index()][1],
scores[select_index()][1],
prob_swap=breeding_rate),
pc, prob_change=mutation_rate))
else:
# 加入一个随机节点,以增加种群的多样性
new_pop.append(make_random_tree(pc))
population = new_pop
scores[0][1].display()
return scores[0][1]
def get_rank_function(dataset):
'''排序函数
'''
def rank_function(population):
scores = sorted([(score_function(t, dataset), t) for t in population], key=lambda x:x[0])
return scores
return rank_function
解决问题:用遗传编程自动生成一个能够拟合特定数据集的函数
现在,我们可以使用上面的程序来解决一个实际中的问题了——自动生成一个能够拟合特定数据集的函数。
让我们先生存一个数据集:
def hidden_function(x, y):
'''用来构造数据集的公式,即要求的正解之一
'''
return x**2+2*y+3*x+5
def build_hiddenset():
rows = []
for i in range(200):
x = randint(0, 40)
y = randint(0, 40)
rows.append([x,y,hidden_function(x,y)])
return rows
现在数据集和程序都有了,让我们用遗传编程来生成这个程序:
rf = get_rank_function(build_hiddenset())
evolve(2, 500, rf, mutation_rate=0.2, breeding_rate=0.1, pexp=0.7, pnew=0.1)
# 输出
21930
5042
4917
1975
1975
1200
1200
807
585
427
191
108
0
add
add
add
p1
0
add
multiply
p0
p0
subtract
p1
subtract
1
multiply
subtract
p0
if
p1
is_greater
p0
subtract
p0
if
p1
0
subtract
5
p0
p1
3
6
从上面可以看到,我们的程序很好的生成了一个拟合数据集的函数。
多样性的重要性
对于遗传编程,我们还需要再谈一个关键问题,即多样性问题。
我们看到evolve函数中,会将最优的个体直接进入下一代,除此之外,对排名之后的个体也会按照比例和概率选择性地进行复制和修改以形成新的种群,这种做法有什么意义呢?
最大的问题在于,仅仅选择表现最优异的少数个体,很快就会使种群变得极端同质化(homogeneous),或称为近亲交配。尽管种群中所包含的题解,表现都非常不错,但是它们彼此间不会有太大的差异,因为在这些题解间进行的交叉操作最终会导致群内的题解变得越来越相似。我们称这一现象为达到局部最大化(local maxima)。
对于种群而言,局部最大化是一种不错的状态(即收敛了),但还称不上最佳的状态。因为处于这种状态的种群里,任何细小的变化都不会对最终的结果产生太大的变化。这就是一个哲学上的矛盾与对立,收敛稳定与发散变化是彼此对立又统一的,完全偏向任何一方都是不对的。
事实表明,将表现极为优异的题解和大量成绩尚可的题解组合在一起,往往能够得到更好的结果。基于这个原因,evolve提供了两个额外的参数,允许我们对筛选进程中的多样性进行调整。
通过降低probexp的值,我们允许表现较差的题解进入最终的种群之中,从而将”适者生存(survival of fittest)“的筛选过程调整为”最适应者及其最幸运者生存(survival of the fittest and luckiest)“
通过增加probnew的值,我们还允许全新的程序被随机地加入到种群中
这两个参数都会有效地增加进化过程中的多样性,同时又不会对进程有过多的扰乱,因为,表现最差的程序最终总是会被剔除掉的(遗传编程的马尔科夫收敛性)。
小结
可以看到,遗传编程和遗传算法思想是非常接近的,两者的不同在于其基因型的表示不同:遗传算法中基因型表示的是参数,而遗传编程中基因型表示的是一个程序,这也是为什么遗传编程能自动生成算法了。
此外,和梯度驱动的SGD优化算法相比,遗传编程每次的迭代优化并不明确朝某个方向前进,而是被动由环境来进行淘汰和筛选,所以是一种环境选择压驱动的优化算法。