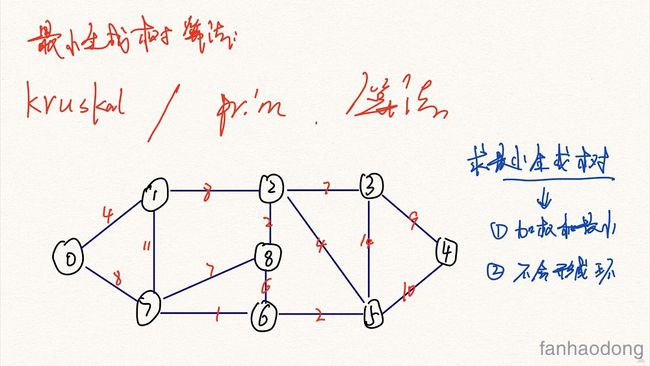
什么是最小生成树
一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边。最小生成树可以用kruskal(克鲁斯卡尔)算法或prim(普里姆)算法求出。
最小权重生成树又是什么
在一给定的无向图G = (V, E) 中,(u, v) 代表连接顶点 u 与顶点 v 的边(即),而 w(u, v) 代表此边的权重,若存在 T 为 E 的子集(即)且为无循环图,使得
的 w(T) 最小,则此 T 为 G 的最小生成树。
最小生成树其实是最小权重生成树的简称。
实际应用场景
例如:要在n个城市之间铺设光缆,主要目标是要使这 n 个城市的任意两个之间都可以通信,但铺设光缆的费用很高,且各个城市之间铺设光缆的费用不同,因此另一个目标是要使铺设光缆的总费用最低。这就需要找到带权的最小生成树。
算法实现
我们首先看我们的无向图 , 需要找到一个最小权重生成树
kruskal 算法
其基本思想就是把每条边都拿出来, 然后按照权重排序, 将这些边组合起来, 要求的是组合过程中不可以形成环, 形成环则放弃这条边
基本实现就是这个了, 打错的是不符合要求的. 到最后就会形成最小权重生成树
Prim 算法
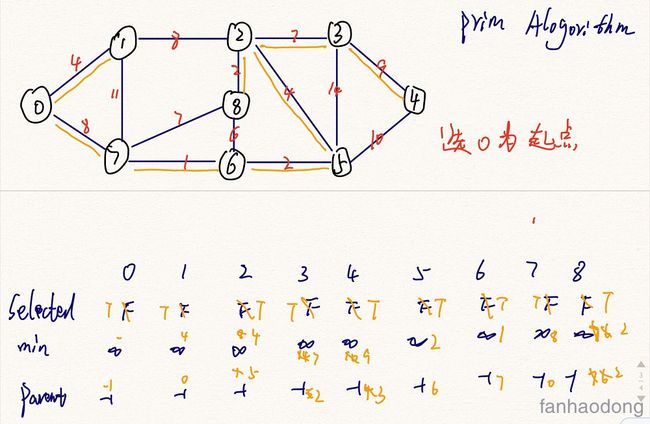
其基本思想就比较麻烦, 我们先看一张图
这里有四行数据,
第一行各个节点.
第二行是节点是否被选中
第三行是节点与父亲节点之间的距离(权重) , 比如 a-b ,如果a被选了,那么 b的父亲就是a,就是这个意思,ab之间的权重就是这个值, 而且b不一定只有一个父亲
第四行就是父亲节点是谁了
所以开始吧
我们首先以0位起始位置 , 0标记为true, 开始往前推进, 0和1,7连着. 0-7=8,0-1=4 , 所以这一次选0-1 , 此时 标记1为true ,
01节点连着的有 0-7=8,1-7=11,1-2=8 ,此时0-7与1-2相同, 此时选择父节点小的为选择对象 , 此时将7标记为true.
071 节点连着 1-2=8 , 7-6=1 , 7-8=7 , 所以选择 7-6 ,标记6为true , 就一直标记到全部为true为止.
这个思路就是我上述讲的.
如果你还是不理解可以看看这个视频 , 链接 : https://www.bilibili.com/video/av47042691?from=search&seid=15424121794388295524