2020/2/3

今日学习

1. linux脚本编程 3h

2. 补ML代码 3h

3. 项目 3h

---

linux

文件系统管理

1,2,3,4只能给主分区，逻辑分区从5开始

格式化：为了写入文件系统

---

shell编程

#！bin/bash 标识， 说明这是一个shell脚本， 不能省略

cat -A 查看文件完整格式，window中的换行符和linux不一样， 导致windows中写的脚本不能在linux中运行

格式转换 dos2unix

别名alias vi='vim'【临时】 删除unalias

echo $PATH 查看path变量

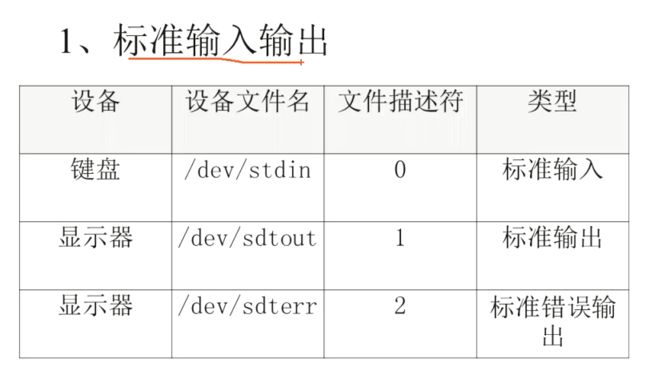
重定向， 输入由屏幕转到文件，文件输入替代键盘

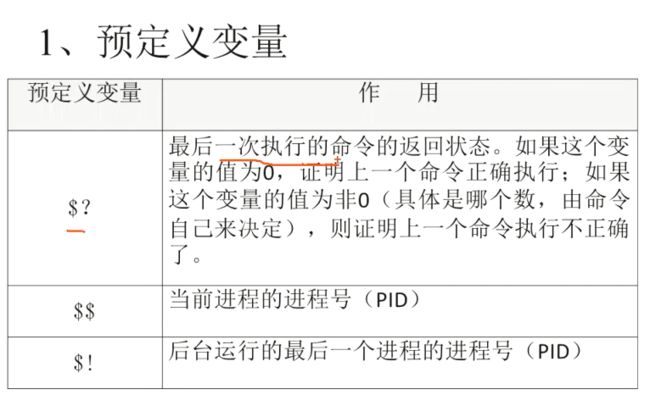
set 查看变量； unset 删除变量

环境变量：全局； bash， dash等shell嵌套--查看pstree

路径添加 PATH="$PATH":/home/hichens/sh

自定义操作目录

read -s -t 10 -p "input age: " age

ML学习

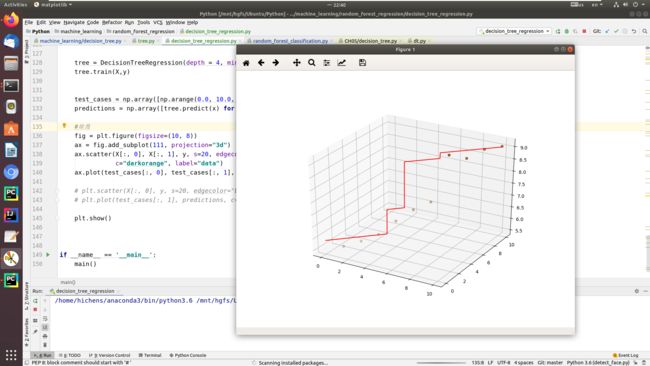
这个代码之所以写了这么久， 我觉得自己主要是对树形结构不了解，递归抓住三点：1.递归的入口；2.递归的方式；3.递归的出口

'''
Implement the decision_tree to adjust more than 1 dimension
'''

import  numpy as np
import  matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

class DecisionTreeRegression():
    def __init__(self, depth = 5, min_leaf_size = 5):
        self.depth = depth
        self.min_leaf_size = min_leaf_size
        self.left = None
        self.right = None
        self.prediction = None

        self.j = None
        self.s = None


    def mean_squared_error(self, labels, prediction):

        if labels.ndim != 1:
            print("Error: Input labels must be one dimensional")

        return np.mean((labels - prediction) ** 2)

    def train(self, X, y):
        if X.ndim == 1:
            X = X.reshape(-1, 1)

        if y.ndim != 1:
            print("Error: Data set labels must be one dimensional")
            return

        #控制最小叶子
        if len(X) < 2 * self.min_leaf_size:
            self.prediction = np.mean(y)
            return

        #深度为一
        if self.depth == 1:
            self.prediction = np.mean(y)
            return

        j, s, best_split, _ = self.split(X, y)

        if s != None:
            left_X = X[:best_split]
            left_y = y[:best_split]
            right_X = X[best_split:]
            right_y = y[best_split:]

            self.s = s
            self.j = j
            self.left = DecisionTreeRegression(depth = self.depth - 1, min_leaf_size = self.min_leaf_size)
            self.right = DecisionTreeRegression(depth = self.depth - 1, min_leaf_size = self.min_leaf_size)

            #左右递归
            self.left.train(left_X, left_y)
            self.right.train(right_X, right_y)

        else:
            self.prediction = np.mean(y)

        # 出口
        return

    def squaErr(self, X, y, j, s):
        mask_left = X[:, j] < s
        mask_right = X[:, j] >= s
        X_left = X[mask_left, j]
        X_right = X[mask_right, j]

        c_left = np.mean(y[mask_left])
        c_right = np.mean((y[mask_right]))

        error_left = np.sum((X_left - c_left) ** 2)
        error_right = np.sum((X_right - c_right) ** 2)
        return error_left + error_right


    def split(self, X, y):
        min_j = 0
        min_error = np.inf

        for j in range(len(X[0])):
            X_sorted = np.sort(X[:, min_j])  # 不改变X
            slice_value = (X_sorted[1:] + X_sorted[:-1]) / 2
            min_s = X[0, min_j] + X[-1, min_j]
            min_s_index = slice_value[0]
            for s_index in range(len(slice_value)):
                error = self.squaErr(X, y, j, slice_value[s_index])
                if error < min_error:
                    min_error = error
                    min_j = j
                    min_s = slice_value[s_index]
                    min_s_index = s_index

            return  min_j, min_s, s_index, min_error

    def predict(self, x):
        # to avoid a number
        if x.ndim == 0:
            x = np.array([x])

        if self.prediction is not None:

            return self.prediction

        elif self.left or self.right is not None:

            if x[self.j] >= self.s:
                return self.right.predict(x)
            else:
                return self.left.predict(x)
        else:
            print("Error: Decision tree not yet trained")
            return None

def main():

    X = np.array([[1, 1], [2, 2], [3, 3], [4, 4], [5, 5], [6, 6], [7, 7], [8, 8], [9, 9], [10, 10]])
    y = np.array([5.56, 5.70, 5.91, 6.40, 6.80, 7.05, 8.90, 8.70, 9.00, 9.05])



    tree = DecisionTreeRegression(depth = 4, min_leaf_size = 2)
    tree.train(X,y)


    test_cases = np.array([np.arange(0.0, 10.0, 0.01), np.arange(0.0, 10.0, 0.01)]).T
    predictions = np.array([tree.predict(x) for x in test_cases])

    #绘图
    fig = plt.figure(figsize=(10, 8))
    ax = fig.add_subplot(111, projection="3d")
    ax.scatter(X[:, 0], X[:, 1], y, s=20, edgecolor="black",
               c="darkorange", label="data")
    ax.plot(test_cases[:, 0], test_cases[:, 1], predictions, c='r')

    # plt.scatter(X[:, 0], y, s=20, edgecolor="black", c="darkorange", label="data")
    # plt.plot(test_cases[:, 1], predictions, c="r")

    plt.show()



if __name__ == '__main__':
    main()

代码终于跑出来了。。。这是最小二乘树回归算法， 没想到从一维到多维这么麻烦。