1335. Minimum Difficulty of a Job Schedule

You want to schedule a list of jobs in d days. Jobs are dependent (i.e To work on the i-th job, you have to finish all the jobs j where 0 <= j < i).

You have to finish at least one task every day. The difficulty of a job schedule is the sum of difficulties of each day of the d days. The difficulty of a day is the maximum difficulty of a job done in that day.

Given an array of integers jobDifficulty and an integer d. The difficulty of the i-th job is jobDifficulty[i].

Return the minimum difficulty of a job schedule. If you cannot find a schedule for the jobs return -1.

 

Example 1:

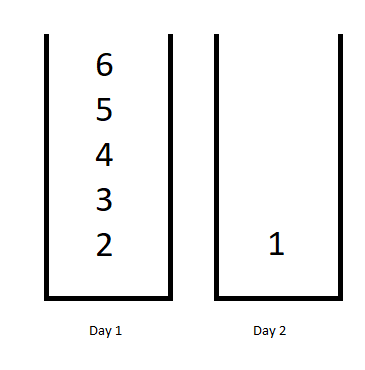
Input: jobDifficulty = [6,5,4,3,2,1], d = 2
Output: 7
Explanation: First day you can finish the first 5 jobs, total difficulty = 6.
Second day you can finish the last job, total difficulty = 1.
The difficulty of the schedule = 6 + 1 = 7 

Example 2:

Input: jobDifficulty = [9,9,9], d = 4
Output: -1
Explanation: If you finish a job per day you will still have a free day. you cannot find a schedule for the given jobs.

Example 3:

Input: jobDifficulty = [1,1,1], d = 3
Output: 3
Explanation: The schedule is one job per day. total difficulty will be 3.

Example 4:

Input: jobDifficulty = [7,1,7,1,7,1], d = 3
Output: 15

Example 5:

Input: jobDifficulty = [11,111,22,222,33,333,44,444], d = 6
Output: 843

 

Constraints:

• 1 <= jobDifficulty.length <= 300
• 0 <= jobDifficulty[i] <= 1000
• 1 <= d <= 10

题目的意思是给了一个数组，要求分成d组，并且满足每组最大值的和sum最小。

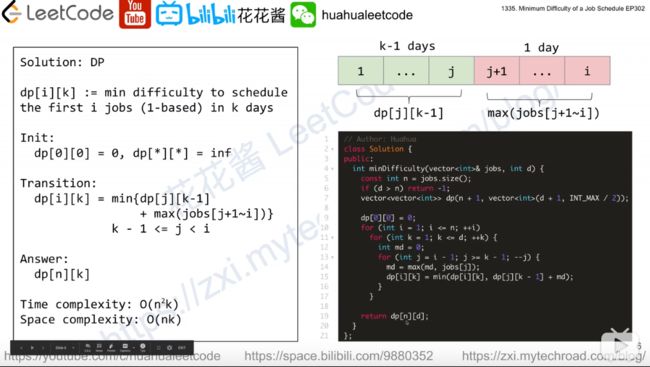
class Solution {
    public int minDifficulty(int[] jobDifficulty, int d) {
        int n = jobDifficulty.length;
        int[][] dp = new int[n + 1][d + 1];
        if(d > n) return -1;
        for(int i = 0; i <= n; i++) Arrays.fill(dp[i], Integer.MAX_VALUE / 2);
        dp[0][0] = 0;
        
        for(int i = 1; i <= n; i++){
            for(int k = 1; k <= d; k++){
                int md = 0;
                for(int j = i - 1; j >= k - 1; j--){
                    md = Math.max(md, jobDifficulty[j]);
                    dp[i][k] = Math.min(dp[i][k], dp[j][k - 1] + md);
                }
            }
        }
        return dp[n][d];
    }
}

 要求最小值，那就要给dp数组初始化大一些，这里选择Integer.MAX_VALUE/2就可以。然后dp[0][0] = 0, 因为后面的值都是由此计算得来。

外面两层循环意思是k天schedule了i件job的最小sum。

然后每次计算dp【i】【k】之前都要重新计算后面的maxdifficult，作为最后一天的值。

里层循环从后往前算，这算一个小技巧，因为从前往后算更新dp的时候每次都要重复计算max值，从后往前算就不用，记录一次就可以了。

首先j >= k-1保证有活能分配，然后j又一定是小于i的，所以得到了界限

 

  

 https://www.bilibili.com/video/av85347641