DT系统的特点:
- 较CT系统来说,DT系统较为简单;(毕竟代数比微积分简单)
- DT和CT的分析方法类似;
- DT系统与电子电路和电脑有密切的关系;
DT系统的表示方法:
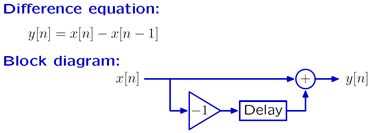
- 差分方程
- 框图
右移操作符R
将一个信号整体右移本质上就是对延迟了这个信号。信号与系统中引入了操作符R来表示将整个离散信号右移一个时间单位。简单的来说就是使用RX表示x[n-1],而使用R^2表示x[n-2]。这样能将差分方程编程多项式代数。
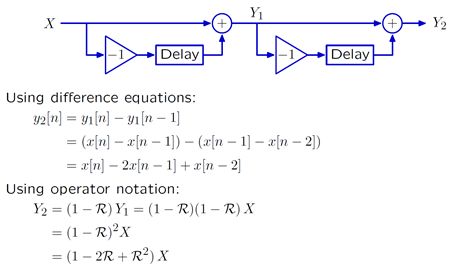
下面列举一个串联系统的例子
使用差分方程的方式表示,通过层层带入得到的结果和使用R操作符的效果一致。需要注意的是,在R操作符表示时,使用乘法的方式来表示两个串联的系统。而且在使用R操作符时,我们可以使用代数中的分配、结合和交换律。
下面举个简单的例子,R操作符表示方法中为什么能使用分配律。
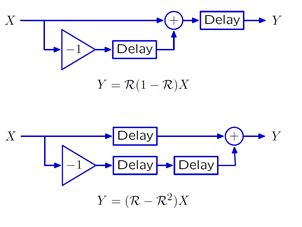
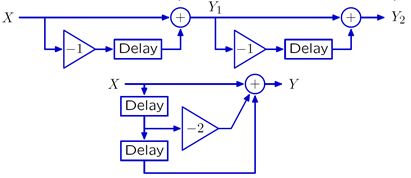
正因为可以使用分配、结合和交换的方法进行等价变形,这暗示着系统可能存在多种等价形式。可使用上述方法验证下面两个系统是等价的,即给定任意相同的输入这两个系统必定给出完全相同的输出。
需要注意的是以为有Delay的存在,因此系统中存在多个状态。只有在这些状态都为0时才能保证两个等价的系统有相同的效果。
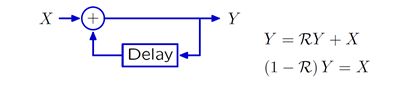
反馈系统
上述例子中信号箭头方向都是从输入指向输出的,这种系统对应的框图都是非循环图,不存在环。下面举个存在环的系统例子。
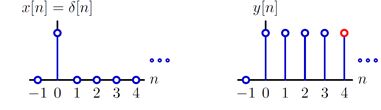
这种情况下,系统的差分方程中存在y[n-1],在R操作符表示法中,存在RY。上述系统对采样信号的相应为离散阶跃信号,具体如下。
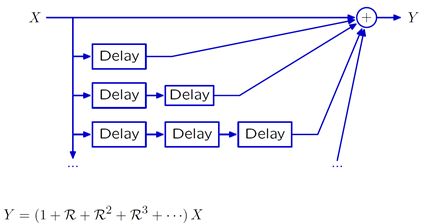
根据等比级数的相关结论,上述这个都有反馈的系统可等效为下列系统。
在上述例子中,该系统的输入信号即使为有限长的序列,其输出信号仍然是无限长的序列。若系统的输出序列无法收敛到0这被称为发散。
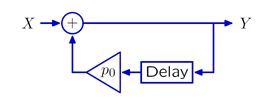
观测上面这个系统可知,若p0大于等于1则该系统不收敛;若p0严格小于1则该系统收敛。该系统的的输出信号为几何序列。
有什么系统的方法来判断一个系统是否发散?