二分是在历年考试中容易出D1T1和D2T1的简单题,是尽量需要满分拿到的知识点,也是难题的优化基础——王主任
二分
二分法指的是在有序的一段区间内,先取一个中间值,判定一下正确答案在中间值的左边还是右边,然后接着再二分,直到找到答案为止
二分的优越性
二分相对于暴力枚举来讲,判定次数会显著变少。具体来说,如果暴力枚举期望是O(N)次,那么二分只需要O(logN)次就可以得出答案
二分查找和线性查找23的位置:
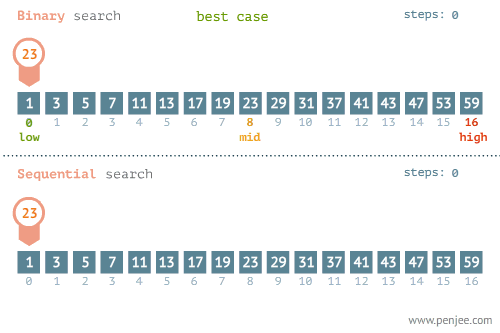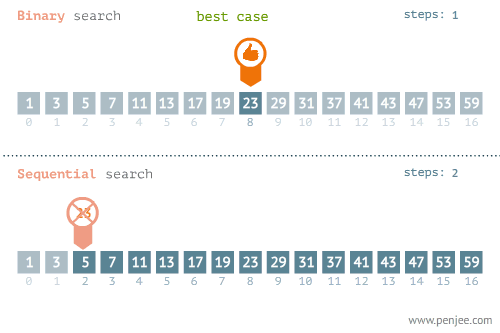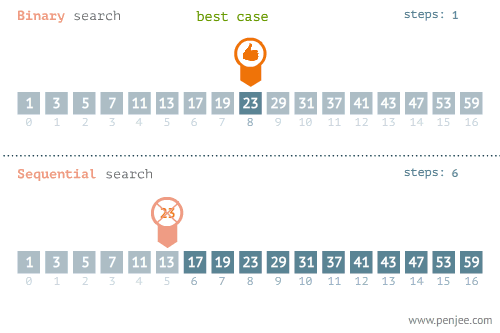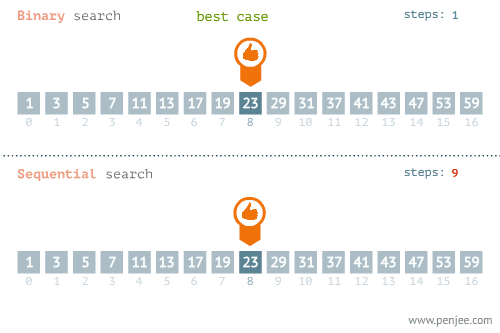
二分查找和线性查找1的位置:
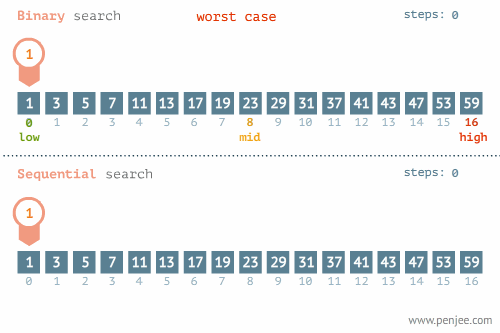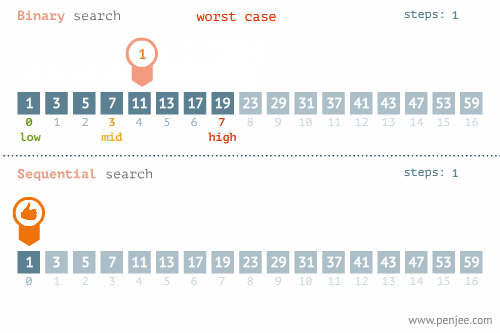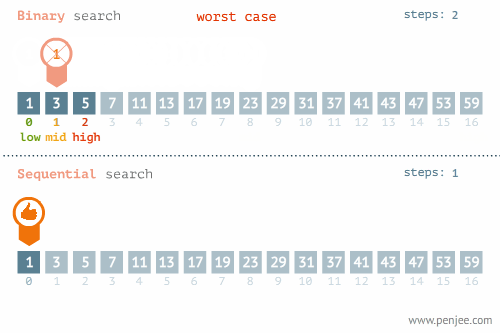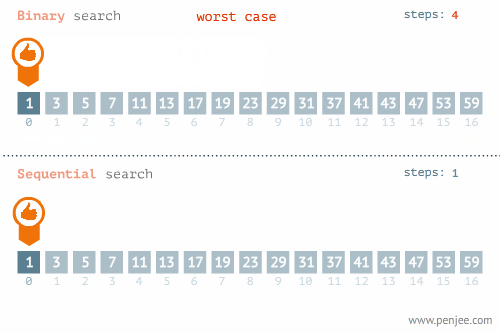
一般来讲我们会在以下情况用到二分:
- 求单调函数的零点
- 求一堆东西的最小值最大是多少
- 很难直接算出答案,但是很好判定答案合不合法
说到二分就离不开二分的常见题型二分答案
顾名思义二分答案就是在可能的答案区间里通过二分法来查找答案
代码框架:
while(l二分答案的具体运用
我们来看一些例题
进击的奶牛 luogu1824 :
题目描述
Farmer John建造了一个有N(2<=N<=100,000)个隔间的牛棚,这些隔间分布在一条直线上,坐标是x1,...,xN (0<=xi<=1,000,000,000)。
他的C(2<=C<=N)头牛不满于隔间的位置分布,它们为牛棚里其他的牛的存在而愤怒。为了防止牛之间的互相打斗,Farmer John想把这些牛安置在指定的隔间,所有牛中相邻两头的最近距离越大越好。那么,这个最大的最近距离是多少呢?
输入格式
第1行:两个用空格隔开的数字N和C。
第2~N+1行:每行一个整数,表示每个隔间的坐标。
输出格式
输出只有一行,即相邻两头牛最大的最近距离。
输入输出样例
输入
5 3
1
2
8
4
9
输出
3
要求相邻两头牛最大的最近距离,很显然要用二分答案。根据二分答案的思想,我们要确定的距离区间左端点就是最小值0,右端点就是最大值,也就是编号最大的牛棚减去编号最小的牛棚。之后对这个区间进行二分答案。
#include
using namespace std;
const int N=1e6+9;
int a[N],n,c;
bool check(int m){
int cnt=1;//第一个牛棚已经算在内
int x=1;
for(int i=1;i<=n;i++)
if(a[i]-a[x]>=m) {//如果有满足当前答案距离的牛棚
cnt++;
x=i;
}
if(cnt>n>>c;
for(int i=1;i<=n;i++){
cin>>a[i];
}
sort(a+1,a+n+1);
int l=1,r=a[n]-a[1];
while(l+1!=r){
int m=(l+r)/2;
if(check(m)) r=m;
else l=m;
}
cout< 一元三次方程求解 luogu1024 :
题目描述
有形如:$ax^3+bx^2+cx^1+dx^0=0$ 这样的一个一元三次方程。给出该方程中各项的系数(a,b,c,d均为实数),并约定该方程存在三个不同实根(根的范围在-100−100至100100之间),且根与根之差的绝对值≥1。要求由小到大依次在同一行输出这三个实根(根与根之间留有空格),并精确到小数点后22位。
提示:记方程f(x)=0,若存在两个数$x_1$和$x_2$,且$x_1$<$x_2$,f($x_1$)×f($x_2$)<0,则在($x_1$,$x_2$)之间一定有一个根。
输入格式
一行,4个实数A,B,C,D
输出格式
一行,3个实根,并精确到小数点后2位。
输入输出样例
输入
1 -5 -4 20
输出
-2.00 2.00 5.00
题目中已经给定了答案区间[-100,100],我们对其进行二分答案,在区间内每次枚举两个点,根据零点存在性定理,若存在零点则进行二分,二分出三个答案后退出程序
#include
#include
#include
#include
#include
#define db double
using namespace std;
db a,b,c,d,f1,f2;
int cnt=0;
db check(db x){
return a*x*x*x+b*x*x+c*x+d;
}
int main()
{
cin>>a>>b>>c>>d;
db l,r,mid;
for(db i=-100;i<=100;++i){
f1=check(i);
f2=check(i+1);
if(!f1){//如果f1对应的函数值为零
printf("%.2lf ",i);
cnt++;
}
if(f1*f2<0){//如果f1,f2之间存在零点
l=i,r=i+1;
while(r-l>=0.001){//若要精确到0.01,ε应多一位
mid=(l+r)/2;
if(check(mid)*check(r)>0) r=mid;
else l=mid;
}
printf("%.2lf ",r);
cnt++;
}
if(cnt==3) break;
}
return system("pause");
} 对于 NOIP 中的分治,难点一般会集中在二分上,所以平时要加大对二分的训练。
我的博客:https://www.cnblogs.com/Wuhen-GSL/