逻辑回归
场景简介:使用逻辑回归实现对鸢尾花的分类预测。
基于python基本库的实现
模型说明
逻辑回归是一个分类模型,根据特征值来预测该样本归属哪一类。
逻辑回归的预测方程式(模型函数)为:
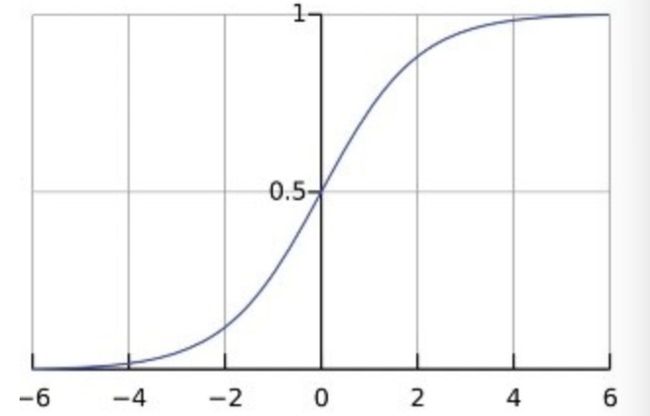
它的函数图如下:
0<=h(θ) <=1
该函数就是逻辑回归的,也叫做
X 为特征向量,θ的就是我们要学习的参数,shape为(n_x,1)
它的预测逻辑一般为:h(θ) >0.5 为正类,h(θ) <0.5 为负类。
当然0.5 这个值也是可以调整的
逻辑回归一般一次只区分两类,所以若要区分多个类(比如k个),则需要建立k或k-1个分类器。
代价函数与梯度下降
逻辑回归用于二分类,y的取值为:(0:负类 1:正类)
我们的模型函数得出的其实就是一个概率值,概率大于0.5归于正类,概率小于0.5 ,get_ipython于负类。
所以y的联合概率分布为:
我们当然是希望L(θ)越大越好。这就是我们的目标。
因为在梯度下降中,我们需要目标函数是凸函数,具有一个极小值。
所以我们要取负,因为L(θ)是一个连乘,我们将其取对数log,将连乘转为求和,方便计算。即:
我们的目标就变成最小化 J(θ)
有了上述,我们就可以来实现逻辑回归了
变量说明
对所用到的变量做一个统一说明,方便检查。
θ·X = W·X+b
设:
m: 样本个数
nx:特征维度
θ:(
则:
X的shape 为:(m,nx) ,我们会在X的前面加一列全为1的,所以实际X为:(m,nx)
y的shape为:(m,1)
θ 的shape = (nx+1)
实现
Package
import numpy as np
from utils import calc_accuracy_class
from utils import fl_score
from sklearn import datasets
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
import pandas as pd
加载数据
X,y = datasets.load_iris(return_X_y=True)
y = y.reshape(-1,1)
#将数据分为训练集和测试集
train_X,test_X,train_y,test_y = train_test_split(X,y,test_size = 0.20,random_state = 1)
print(f"train_X的大小为:{train_X.shape}")
print(f"tain_y的大小为:{train_y.shape}")
print(f"test_X的大小为:{test_X.shape}")
print(f"test_y的大小为:{test_y.shape}")
train_X的大小为:(120, 4)
tain_y的大小为:(120, 1)
test_X的大小为:(30, 4)
test_y的大小为:(30, 1)
#标准化
def nomalize(X,axis):
mean = np.mean(X,axis)
std = np.std(X,axis)
return (X-mean)/std, mean,std
#将数据标准化
train_X,mean,std = nomalize(train_X,axis=0)
test_X = (test_X-mean)/std
#插入一列全为1的表示x0
train_X = np.insert(train_X,0,1,axis=1)
test_X = np.insert(test_X,0,1,axis=1)
print(train_X.shape)
print(test_X.shape)
(120, 5)
(30, 5)
初始化参数
def init_parameters(n):
theta = np.random.randn(n,1)
return theta
Sigmoid函数
def sigmoid(z):
return 1/(1+np.exp(-z))
代价函数
costs =
def compute_cost(y_hat,y):
'''
y_hat --当前阶段的预测值
y -- 真实值
'''
m = y.shape[0]
cost = -np.sum(y*np.log(y_hat)+(1-y)*(np.log(1-y_hat)))/m
return cost
梯度下降
costs =
设z=θ·x
可解得:
dz = (y'-y)
所以:
dθ = x.T·(y'-y)
def gradient_descent(X,y_hat,y,theta,lr):
'''
y_hat --当前阶段的预测值
y -- 真实值
lr -- 学习速率
'''
d_theta = np.dot(X.T,y_hat-y)
theta = theta - lr*d_theta
return theta
基本逻辑单元
基本逻辑单元,处理二分类。多分类不过由多个基本逻辑单元构成
class BasicLogicUnit:
def __init__(self,X,y,category):
'''
X -- 训练样本,shape:(m,nx)
y -- 0 or 1 shape:(m,1)
category -- 真正的类别,即y为1时,所代表的类别
'''
self.X = X
self.y = y
self.category = category
self.theta = init_parameters(self.X.shape[1])
def fit(self,lr,steps):
'''
训练
'''
m,n_x = self.X.shape
costs = []
for step in range(steps):
z = np.dot(self.X,self.theta)
y_ = sigmoid(z)
loss = compute_cost(y_,self.y)
costs.append(loss)
self.theta = gradient_descent(self.X,y_,self.y,self.theta,lr)
if step % 50 == 0:
print(f"\nAfter {step} step(s),cost is :{loss}")
return costs
def predict(self,X):
'''
预测
'''
z = np.dot(X,self.theta)
return sigmoid(z)
逻辑回归模型
根据训练数据,整合多个逻辑单元进行预测
class LogicRegressionModel:
def __init__(self):
self.logic_unit_list = []
def fit(self,tain_X,train_y,learning_rate =0.05,steps = 500):
classes = set(np.squeeze(train_y))
n_classes = len(classes)
m,n_x = train_X.shape
#根据分类的类别,一个个使用逻辑单元进行分类训练
for c in classes:
unit_train_y = np.where(train_y == c,1,0)
logic_unit = BasicLogicUnit(train_X,unit_train_y,c)
self.logic_unit_list.append(logic_unit)
costs = logic_unit.fit(learning_rate,steps)
#绘制损失曲线
plt.xlim(0,steps)
plt.plot(costs)
plt.xlabel("steps")
plt.ylabel("costs")
#plt.title(f"c = {self.category}")
y_pred = logic_unit.predict(train_X)
y_pred = np.where(y_pred > 0.5,1,0)
acc = calc_accuracy_class(y_pred,unit_train_y)
print(f"{c}类的准确率为:{acc}")
def predict(self,X):
m = X.shape[0]
#为了可视化,我们将其以DataFrame的形式输出
zeros= np.zeros((m,1),dtype=int)
results_pd = pd.DataFrame(zeros,columns=["result"])
for logic_unit in self.logic_unit_list:
prob_y = logic_unit.predict(X)
results_pd[logic_unit.category] = prob_y
max_indexs = np.argmax(np.array(results_pd),axis=1)
y_ = np.array(results_pd.columns)[max_indexs]
y_ = y_.T
results_pd["result"] = y_
print(results_pd.head())
return y_
model = LogicRegressionModel()
model.fit(train_X,train_y,learning_rate=0.05,steps=40)
After 0 step(s),cost is :1.3471522333761674
0类的准确率为:1.0
After 0 step(s),cost is :1.0414187137571345
1类的准确率为:0.7166666666666667
After 0 step(s),cost is :2.771585424064274
2类的准确率为:0.975
logits = model.predict(train_X)
fl_score(np.squeeze(logits),np.squeeze(train_y))
acc = calc_accuracy_class(logits,train_y)
print("准确率为:%g"%(acc))
result 0 1 2
0 1 4.773352e-03 0.336848 0.114623
1 2 1.197002e-07 0.775613 0.997784
2 1 4.206618e-03 0.727077 0.010902
3 2 2.973954e-06 0.580281 0.991170
4 2 4.080572e-06 0.269009 0.997358
0 类的fl_score 为:1.0
1 类的fl_score 为:0.918918918918919
2 类的fl_score 为:0.9318181818181818
准确率为:0.95
from utils import calc_accuracy_class
logits = model.predict(test_X)
fl_score(np.squeeze(logits),np.squeeze(test_y))
acc = calc_accuracy_class(logits,test_y)
print("准确率为:%g"%(acc))
result 0 1 2
0 0 0.999999 0.003394 1.241299e-08
1 1 0.038971 0.490671 2.159986e-03
2 1 0.001926 0.494310 6.139991e-02
3 0 0.999997 0.002576 7.951771e-08
4 2 0.000129 0.144131 9.728652e-01
0 类的fl_score 为:1.0
1 类的fl_score 为:0.8181818181818181
2 类的fl_score 为:0.7499999999999999
准确率为:0.866667
结果还ok,稍微有点过拟合。
完整代码地址:https://github.com/huanhuang/logicRegression.git