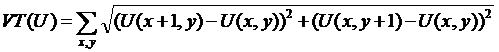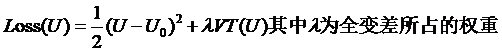前言:最近在看python计算机视觉,看到了ROF降噪模型,但教程中没有详细解释ROF的原理,所以打算将自己的心得写下来,分享一下,也请大家指出问题,一起学习,因为水平有限,可能会有错误,欢迎指正
1.ROF简介
ROF模型在92年由Rudin,Osher,Fatemi提出,他们提出“ 最小化 ‘全变差’ ” 可以有更好的去除图像中噪声的效果。
2.ROF降噪原理
1.规定一些符号
2.什么是全变差
这里介绍了什么是全变差
在原论文中,全变差是图像差分的L1范数,即
3.将问题转化为数学问题
原论文中还有如下约束,
将问题描述为,在上式的约束下,使TV(U)最小。
作者在论文中用到了欧拉-拉格朗日方程,由于我目前还没有学过泛函数分析,所以采用了梯度下降法(Gradient Descent)
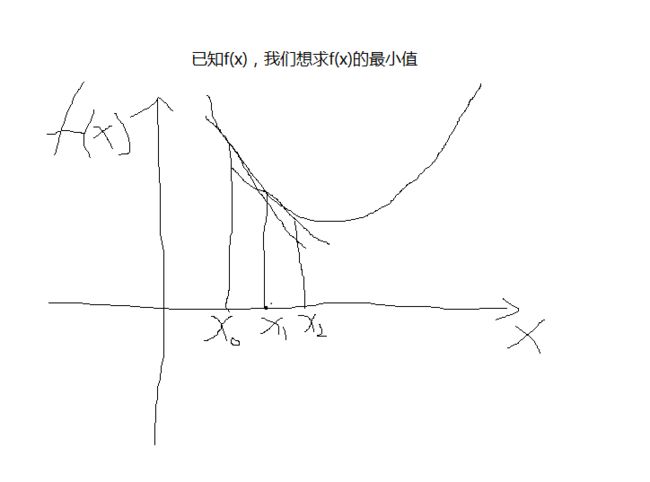
下面先解释一下什么是梯度下降法:
迭代公式为:
如果我们想求最大值,只需将迭代公式中的减号变为加号
对梯度下降法比较直观的解释是:想象你站在一座山的山腰处,你想要最快的下山,一种方法就是沿着坡度最大的方向走(如果实在太陡了,走不了,那你就飞吧。。。),通过这个例子,我们能发现一个问题,那就是梯度下降法可能陷入局部最优(陷入某一个山谷中),但作者在论文中提到,这种局部最优更接近于图像的处理过程(可以理解为这种局部最优是距离噪声图像最近的一个最优解,如果全局最优的话,可能会丧失掉太多的图像信息)
4.如何求(迭代)出清晰图像
首先,我们要先定义一个函数,这个函数能将优化问题和约束条件结合起来,我们称这个函数为损失函数
通过上边的讲解,我们知道只要求出Loss(U)对于U的导数(更准确地说,应是差分,因为图像不是连续的函数),就能通过梯度下降法,迭 代出清晰图像!
3.代码实现
# -*- coding: utf-8 -*-
"""
Created on Tue Oct 17 21:33:43 2017
@author: ningminghao
"""
from numpy import *
from pylab import *
from PIL import Image
def denoise(im,U_init,tau=0.5,tv_weight=30,max_iteration=10):
#im,U_init为含噪音的图像,tau与步长有关,tv_weight为全变差所占的权重λ,max_iteration为最大的迭代次数
m,n = im.shape
U = U_init
Px = im
Py = im
count = 0
while(count Uold = U GradUx = roll(U,-1,axis=1)-U #这里就是差分ux,如果对axis的选取有疑惑,本文后边提供了一个链接 GradUy = roll(U,1,axis = 0)-U #这里就是差分uy #roll()函数,其实就相当于将矩阵移动,类似于无界模式的贪吃蛇,在最边缘位置的数会移动到对面 NormNew = maximum(1,sqrt(GradUx**2+GradUy**2))#为了防止出现分母为0 Px = GradUx/NormNew Py = GradUy/NormNew RxPx = roll(Px,-1,axis=1) RyPy = roll(Py,-1,axis=0) DivP = (RxPx-Px)+(RyPy-Py) step = tau*(exp(-count*2/(max_iteration))+0.1)#有点模拟退火的意思 U = Uold - step*((Uold-im)+tv_weight*DivP) #梯度下降 error = linalg.norm(U-Uold)/sqrt(n*m) if (count%10==0): print('step:',step) print('error:',error) count+=1 return U,U-U_init from numpy import random from scipy.ndimage import filters im = zeros((500,500)) #建立一个图形,外黑,中灰,内白 im[100:400,100:400] = 128 im[200:300,200:300] = 255 noise = 30 *random.standard_normal((500,500)) #噪声 im = im + noise U,T = denoise(im,im,max_iteration=10,tau=0.5) gray() subplot(121) imshow(im) subplot(122) imshow(U) print(corrcoef(T.flatten(),noise.flatten()))#相关度检验 以上代码完全按照上面的公式推导来的,如果哪里不懂就再看看公式推导 建议手动敲一下上面的代码,相信你会更好的理解 对python的axis有疑惑的点这里 简单的介绍了ROF的数学原理,及迭代公式的推导,介绍了梯度下降,在步长的处理上进行了类似于模拟退火的处理方式(使得前期步长较大,后期步长较小),其实还有一种加入“动量因子”的技术,可以使得梯度下降收敛的更快且更容易接近最优点,有兴趣的可以自己搜索一下 由于这是本人第一篇手打的文章,对于一些排版还不是很熟悉,所以上边的代码不能直接复制(手动卖萌) 最后的最后,由于接触计算机视觉时间并不长,希望大家以批判的眼光看待这篇文章,欢迎指正与讨论4.总结一下