计数问题其实只是组合数学中的一小部分,以上也仅仅介绍了比较经典的结论。组合问题复杂多变,它们之间也少有联系,所以把组合数学称作一门学科并不准确。组合难题也会出现在各种益智趣题或竞赛难题中,随随便便就会出现一些未解的难题,所以我们也将止步于此。在结束本课之前,我决定再窥探一下组合问题中的一大类:组合设计。这些问题的关注点在如何布局元素,以满足一些特定要求,它们已然构成了组合学的众多分支。
1. 0-1矩阵
1.1 关联矩阵的秩
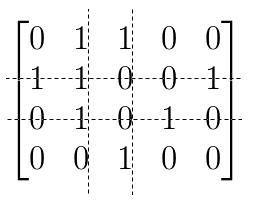
有的问题需要在两个集合\(A,B\)间建立联系,如果把\(A,B\)的元素分别纵横排列,对应位置上以\(0,1\)表示元素是否有关联。这就得到了一个0-1矩阵,当然这里我们并不关注它的代数性质,而仅仅是借用其便捷的形式,来研究满足一定条件的组合问题。0-1矩阵也被称为关联矩阵,它可以是两个集合间的联系(比如集合\(A\)的子集与元素的包含关系),也可以是同一集合中元素的关系(比如图论中的图)。
在讨论关联矩阵时,矩阵的行列的顺序对问题并无影响,为了讨论方便,可以随意交换行或列。好的,现在面对着一个满是\(0,1\)的矩阵\(R\),我们需要讨论些什么问题呢?除了看每个0,1项之外,当然还看到了每一行和每一列,我们把它们都称为矩阵中的线。只要选择足够多的线,总可以包含所有的\(1\),这些线称为关联矩阵的覆盖。你自然会想到一个有意义的问题:线数最小的覆盖是多少?我们把它定义为矩阵的线秩,记作\(\lambda(R)\)。
换个角度,称矩阵中的一个\(1\)为项,与之相关的有行、列两条线,把不在同一条线上项称为无关项。无关项足够多时,它们的线也可以覆盖关联矩阵,这就有了另外一个有意义的问题:最多可以有多少个无关项?我们把它定义为矩阵的项秩,记作\(\rho(R)\)。因为所有项包含在任意一个线覆盖中,而每条线上最多只能有一个无关项,故首先有\(\rho(R)\leqslant \lambda(R)\)。
反之对于线数为\(\lambda(R)\)的覆盖,设有\(p\)行\(q\)列,下面证明可以在每行、列上取得一个无关的代表项。考察\(p\)行中与\(q\)列不相交的部分,如果不能在其中选出\(p\)个无关的项,则必然可以用小于\(p\)条列线取代这\(p\)条行线。另一部分同样论证,这就证明了总可以选出\(p+q=\lambda(R)\)个无关项,从而有\(\rho(R)\geqslant \lambda(R)\)。这就得到了等式(1),以后可以统称线秩、项秩为秩,线秩和项秩的问题可以互相转化,这从下面的例子和定理中都能看出。
\[\rho(R)=\lambda(R)\tag{1}\]
秩等于行列中较小值的矩阵便称为是满秩的,存在一种满秩的\(n\)阶方阵,它仅有\(n\)个\(1\),每行每列有且仅有一个\(1\)。换个说法,这种矩阵的每行每列之和都是\(1\),若干这种矩阵\(P_k\)的凸线性组合(式(2))也必然满足这一条件。每条线上和都为\(1\)的非负实矩阵被称为双随机矩阵,这是一种很有用的矩阵。
\[P=c_1P_1+c_2P_2+\cdots+c_mP_m,\;\;(c_k>0,\;\sum_{k=1}^mc_k=1)\tag{2}\]
现在反过来问,是不是所有双随机矩阵都有式(2)的凸线性分解呢?这个其实不难,首先双随机矩阵不能被少于\(n\)条线覆盖,故必然是满秩的。选择\(n\)个无关项并取最小值\(c_1\),作关联矩阵\(P_1\)使其仅在这\(n\)个项为\(1\)。作出满足\(P=c_1P_1+(1-c_2)P'_2\)的\(P'_2\),它也是双随机矩阵,但非零项比\(P\)少一个。对\(P'_2\)继续这个过程,有限步后便可得到式(2),结论得证,它被称为Birkhoff定理。
1.2 Hall定理
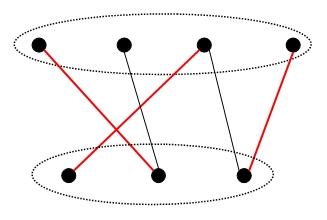
关联矩阵的项秩有一个非常重要的等价描述,把关联矩阵看出是点集\(A,B\)之间的连接,这在图论中被称为二部图。\(A,B\)各选出一个关联的元素\((a,b)\)称为一个匹配,然后继续在剩下的元素中选取匹配,项秩正表示二部图中的最大匹配数。这个模型有很广泛的应用,典型的就是任务分配问题:每个人能胜任某些任务,给一个分配方案,使尽量多的人能做自己胜任的任务。
当然这个问题的第一步先要求矩阵的秩,或者更弱一点,至少我们要找到满秩的判定条件。为了表述方便,下面换一个等价模型,设\(A\)是集合,把\(b\in B\)看成是\(A\)的一个子集,\(a,b\)关联当且仅当\(a\in b\)。\(B\)是集合的集合,一般也称为集系。对于满秩的关联,为每个\(b\)都能找到一个互异的\(a\in b\),它们被称为\(B\)的相异代表系。
对于集系矩阵满秩有一个很显然的必要条件,就是任意\(r\)个子集的并不小于\(r\)。令人惊喜的是,它居然还是个充分条件,该结论被称为霍尔(Hall)定理(式(3))。其实条件本身等价于说,矩阵的零子矩阵总不大于\(r*(|A|-r)\),故零子矩阵的行列和总小于\(|A|\),从而线覆盖数至少为\(|B|\)。这就证明了满秩,论证中用到了线秩在零子矩阵里的等价条件,这也是线秩最常用的方法。
\[\rho(R)=|B|\;\Leftrightarrow\;|b_1\cup b_2\cup\cdots\cup b_r|\geqslant r,\;(\forall b_i\in B,\forall r\leqslant |B|)\tag{3}\]
Hall定理有很高的理论价值,但在实际应用中仍不是很方便,但借助这个定理,我们可以有更强但更方便的条件。比如如果存在\(r>0\),使得矩阵每行至少有\(r\)个\(1\)而每列最多有\(r\)个\(1\),可以证明它满足Hall定理,从而为满秩。其实任选\(s\)行,其中包含至少\(sr\)个\(1\),它们至少要有\(r\)列来覆盖,结论得证。当然实际应用中并不总能找到完美匹配,假设至少有\(d\)个找不到工作,只需再添加\(d\)个虚拟的大家都能做的工作,利用Hall定理也可以得到只有\(d\)个人找不到工作的充要条件是:任意\(r\)个子集的并不小于\(r-d\)。
再来看Hall定理的两个有趣的应用。考察集合\(X\)的的两个分割\(A_1,\cdots,A_n\)和\(B_1,\cdots,B_n\),我们希望找到\(n\)个互异的元素\(x_k\),使得\(x_k\in A_k\)且\(x_k\in B_k\),它们被称为分割的共同代表元组。以\(A_i,B_j\)有非空交集作为关联,问题等同于判断满秩,Hall定理说明满秩的充要条件是:任何\(r\)个\(A_k\)之并最多包含\(r\)个\(B_k\)之并。特别地,当\(|A_k|,|B_k|\)全部相等时,充要条件显然满足,也就是说,集合的任意两个分割数相等的平均分割总存在共同代表元组。
有一种常见的\(m\times n\)阶矩阵,共有\(n\)个不同的元素组成,且每条线上的元素不同。这样的矩阵称为拉丁矩阵,显然有\(m\leqslant n\),当\(m=n\)时称为拉丁方。一个自然的问题是,任何拉丁矩阵是否都能扩展为拉丁方?考察不属于第\(k\)列的元素组成的集合\(A_k\),它们和\(n\)个元素以包含关系建立关联。显然,每个\(A_k\)包含\(n-m\)个元素,而每个元素已经出现过\(m\)次且属于不同的列,故未出现在\(n-m\)列中。直接利用Hall定理的推论,可选出\(A_k\)的相异代表系,以它们组成新的一行,可以继续这个过程,直至构造出拉丁方。
1.3 积和式
对\(m\times n\)阶的关联矩阵\(R\)(\(m\leqslant n\)),一组相异代表系其实就是在每行\(k\)取一个元素\(a_k\),满足\(a_1a_2\cdots a_m=1\)。这就启发我们,对每行的任意选取计算其乘积,并将所有可能的乘积相加,结果便是相异代表系的个数。严格来讲,一种选取就是一个从行数\(k\)到列数的互异映射\(\sigma(k)\),记所有这种映射的集合为\(\Omega\),称式(4)为关联矩阵\(R\)的积和式(permanent)。
\[\text{Per}(R)=\sum_{\sigma\in \Omega}a_{1\sigma(1)}a_{2\sigma(2)}\cdots a_{m\sigma(m)}\tag{4}\]
式(4)的定义与矩阵行列式的定义非常类似,故不难证明积和式也有类似行列式计算的拉普拉斯展开式,这里就不展开阐述了。积和式的计算并不容易,它只有理论价值,对于特殊的形式的关联矩阵可以通过拉普拉斯方法简化计算。积和式一般用于一些计数问题中,这里举一个常见的例子。
考虑将\(n\)个元素重新排列,并限制每个元素出现的位置,这种问题被称为限位排列问题。每个元素和可以出现的位置建立起\(n\times n\)阶关联矩阵,排列的个数显然就是矩阵的积和式。前面多次提到的错位排列问题就是一个特例,它的关联矩阵为\(J_n-I_n\)(\(J_n\)为全\(1\)矩阵),容易得到\(D_n=(n-1)(D_{n-1}+D_{n-2})\),你可以尝试计算其母函数和通项公式。
还有一个经典的限位排列问题,就是著名的“夫妻围坐”问题:\(n\)对夫妻围坐在圆桌边,要求男女相间但夫妻不相邻。可以先让女士入座,问题的难点就是男士入座的坐法数\(U_n\)。记女士\(k\)左手边的位置为\(k\),男士\(k\)就不能坐\(k\)或\(k+1\)(\(k=n\)时为\(1\)),这是个典型的限位排列问题。我们可以轻松地写出关联矩阵\(J_n-I_n-P_n\)(\(P_n\)是\(a_{i(i+1)}=a_{n1}=1\)的矩阵),但它的显式表达式比较难解,这里只给出结论(式(5),试试用容斥原理解决)。
\[U_n=\sum_{k=0}^n(-1)^k\dfrac{2n}{2n-k}\binom{2n-k}{k}(n-k)!\tag{5}\]
1.4 0-1矩阵类
对一个\(m\times n\)阶的关联矩阵\(R\),可以计算每行和每列\(1\)的个数\(p_i,q_j\),向量\(P=(p_1,\cdots,p_m),Q=(q_1,\cdots,q_n)\)被称为行和向量与列和向量。我们自然想问,任意给定\(m\)维向量\(P\)和\(n\)维向量\(Q\),存在以它们为行(列)和向量的关联矩阵吗?首先当然有式(6)成立,这个条件过于平凡,以下把它当做默认条件,并把以\(P,Q\)作为行(列)和向量的所有关联矩阵的集合记作\(R(P,Q)\)。
\[p_1+\cdots+p_m=q_1+\cdots+q_n\tag{6}\]
由于行列可以任意交换,我们事先假定\(p_i,q_j\)都是递减排列的。在具体排列时,先将每行的\(p_k\)个\(1\)全部靠左放置,得到的矩阵记作\(R(P,n)\)。它的列和向量记作\(P^*=(p_1^*,\cdots,p_n^*)\)。\(R(P,n)\)的特点是向左紧凑排列,具体来讲就是任意\(p_1^*+\cdots+p_k^*\)都取到了最大值。为讨论方便,如果两个\(n\)维向量满足式(7),则称\(T\)优超于\(S\)。刚才的讨论说明,\(R(P,Q)\)非空的必要条件是\(Q\prec P^*\)。
\[S\prec T\;\Leftrightarrow\;\sum_{i=1}^ks_i\leqslant\sum_{i=1}^kt_i,\,(k=1,2,\cdots,n)\tag{7}\]
其实\(Q\prec P^*\)也是\(R(P,Q)\)非空的充分条件(式(8),当然还要求(6)成立),它由Ryser和Gale分别单独发现,这里仅描述一下思路,严格证明请看教材。以\(R(P,n)\)为初始状态,第一步将行和最小的\(m-q_1\)行向右平移一列,这样第一列就只有\(q_1\)个\(1\)。去除掉第一列后矩阵仍然是相左紧凑排列的,将余下矩阵的行和最小的\(m-q_2\)行向右平移一列,依次类推便可构造出\(R(P,Q)\)。
\[R(P,Q)\ne\varnothing\;\Leftrightarrow\;Q\prec P^*\tag{8}\]
2. 集系的极值
组合设计问题中还有一类问题,就是在\(X\)的所有子集中选出满足条件的子集构成集系\(B\),并且讨论\(B\)能取到的最值。这类问题花样繁多,大部分也很难解决,残留了大量尚未解决的问题。以我有限的眼光看,这些智力竞逐的游戏并没有广泛的应用领域,这里暂时就不做介绍了,留作后话吧。子集间最简单的关系就是交集和包含,下面从这两方面讨论两个简单的问题。
2.1 相交集系
第一个问题很简单,就是要求集系中的元素两两交集非空,问集系最大为多少?构造两两相交的集系并不难,任取\(x\in X\),所有包含\(x\)的子集便满足条件,其个数是所有子集的一半\(2^{n-1}\)。还能更大吗?对任何子集\(b\in B\),\(b\)和\(\bar{b}\)不能同时选取,故\(2^{n-1}\)已是最大值。
甚至对一个阶小于\(2^{n-1}\)的相交集系\(B\),总可以将其扩展为\(2^{n-1}\)个。因为总存在\(b\)使得\(b,\bar{b}\)都不属于\(B\),如果\(b\)与\(B\)的所有元素都相交,则\(b\)可添加进\(B\)。否则设存在\(b'\in B\)使得\(b\cap b'=\varnothing\),则可证\(B\)中任意元素\(b''\)都满足\(b''\not\subset b\),因为这样的话\(b'\cap b''=\varnothing\),矛盾。既然恒有\(b''\not\subset b\),则必然有\(b''\cap \bar{b}\ne\varnothing\),可将\(\bar{b}\)添加到\(B\)中,结论得证。
如果把条件改成任意三个集合有交集呢?基于开始的构造(总取\(a\)),最多仍然能取到\(2^{n-1}\)个,现在来证明这是唯一的情况。假设\(p\)是满足\(b_1\cap\cdots\cap b_p=b\in B\)的最大值,如果\(p<2^{n-1}\),则易证\(b\cap b_{p+1}\)不属于\(B\),但却与\(B\)中所有元素有交集,矛盾。故\(p=2^{n-1}\),唯一性便容易证明。
2.2 Sperner系
第二个问题可以描述为,集系\(B\)中的元素互不包含,问集系最大为多少?这样的集系也称为Sperner系。既然讨论到包含关系,我们来考察所有满足时(9)的包含链,Sperner系在每条链上最多只能有一个元素。由于包含链上每一步只多一个元素,故包含链总共有\(n!\)条。对任意\(b\in B\),如果\(|b|=k\),则包含\(b\)的链共有\(k!(n-k)!\)条。若记\(B\)中阶为\(k\)元素有\(f_k\)个,由于每条链最多只能包含\(B\)的一个元素,则显然有式(10)左成立,整理后便是式(10)右。
\[\varnothing=b_1\subset b_1\subset\cdots\subset b_n=X,\;\;(|b_{k+1}|-|b_k|=1)\tag{9}\]
\[\sum_{k=1}^{n}(f_k\cdot k!(n-k)!)\leqslant n!\;\Rightarrow\;\sum_{k=1}^{n}\dfrac{f_k}{\binom{n}{k}}\leqslant 1\tag{10}\]
以下记\(m=\lfloor\dfrac{n}{2}\rfloor\),由\(\binom{n}{k}\)的单调性易知\(f_1+\cdots+f_n\leqslant\binom{n}{m}\),等号成立的充要条件是:只有当\(k=m,m+1\)时\(f_k\ne 0\),并且所有链上都有\(B\)中的元素。当\(B\)取所有\(m\)阶子集,或者取所有\(m+1\)阶子集时,都满足等式要求。下面证明其实只能取这两种子集之一,证明中一定要牢记:每条链都有且仅有一个\(B\)的元素。
假设\(m+1\)阶子集只有部分在\(B\)中,则必然可选出\(m+1\)阶子集\(b_1\in B,b_2\not\in B\)。将\(b_1\)向\(b_2\)每次换一个元素地渐变,过程中必有某个时刻有\(b_3\in B,b_4\not\in B\),且\(|b=b_3\cap b_4|=m\)。由\(b_3\in B\)知\(b\not\in B\),但由\(b_4\not\in B\)又有\(b\in B\),矛盾!只就证明了,Sperner系取最大值时,要么全是\(\lfloor\dfrac{n}{2}\rfloor\)阶子集,要么全是\(\lceil\dfrac{n}{2}\rceil\)阶子集,该结论被称为Sperner定理。
【全篇完】