模糊控制中有一个隶属度函数的概念。
是模糊集合中会用到的函数,是一般集合中指示函数的一般化[1]。指示函数可以说明一个集合中的元素是否属于特定子集合。一元素的指示函数的值可能是0或是1,而一元素的隶属函数会是0到1之间的数值,表示元素属于某模糊集合的“真实程度”(degree of truth)。
这次我们编写6种常见隶属度函数(来源:百度文库)的计算程序。
按这个文件命名哦!
membership_function.py
'''
六种常见的隶属度函数
矩阵
梯形
抛物线
高斯
柯西
伽马
'''
from math import exp
import numpy as np
import matplotlib.pyplot as plt
class MembershipDegree(object):
def no_mold(self,mold):
# 选择模式是否存在
print('no this mold: {0} ???\n we have 0/1/2 represent small/medium/large'.format(mold))
exit(1)
def y_array(self,f,x):
y=[]
for xx in x:
y.append(f(xx))
y=np.array(y)
return y
def huahua(self,x,y):
plt.plot(x, y)
plt.ylim(-0.2, 1.2)
plt.xlim(x[0] - (max(x) - min(x)) * 0.1, x[-1] + (max(x) - min(x)) * 0.1)
# plt.axes([x[0]-(max(x)-min(x))*0.1,x[-1]+(max(x)-min(x))*0.1,-0.2,1.2])
plt.grid()
class Matrix(MembershipDegree):
def __init__(self,a,b=None,mold=0):
super().__init__()
if (mold == 1):
assert b != None
self.a=a
self.b=b
self.mold=mold
def matrix(self,x):
a,b,mold=self.a,self.b,self.mold
# 矩阵型
if(mold==1):
# 中间型
if (a<=x<=b):
u = 1
else:
u = 0
elif(mold==0):
# 偏小型
if (x<=a):
u=1
else:
u=0
elif(mold==2):
# 偏大型
if (xb):
u=0
else:
u=(b-x)/(b-a)
elif(mold==2):
# 大
if (x <= a):
u = 0
elif (x > b):
u = 1
else:
u = 1-(b - x) / (b - a)
else:
super().no_mold(mold)
return
return u
class Paracurve(MembershipDegree):
def __init__(self,a,b,c=None,d=None,mold=0,k=3):
super().__init__()
self.a, self.b, self.c, self.d, self.mold,self.k= a, b, c, d, mold,k
self.temp = Trapezoid(a, b, c, d, mold)
def paracurve(self,x):
# k次抛物线 哈哈-->>就是在梯形型基础上对每一个结果k次方
a, b, c, d, mold, k=self.a, self.b, self.c, self.d, self.mold, self.k
u=self.temp.trapezoid(x)**k
return u
class Gauss(MembershipDegree):
def __init__(self,a=0,mold=0,theta=1):
self.a,self.mold,self.theta=a,mold,theta
def gauss(self,x):
a, mold, theta=self.a,self.mold,self.theta
# theta:方差
# a:均值
# 高斯型
f=lambda :exp(-((x-a)/theta)**2)
if(mold==1):
u=f()
elif(mold==0):
if(x<=a):
u=1
else:
u=f()
elif(mold==2):
if(x<=a):
u=0
else:
u=1-f()
else:
super().no_mold(mold)
return
return u
class Cauchy(MembershipDegree):
def __init__(self,a,mold=0,alpha=1,beta=2):
assert alpha > 0 and beta > 0
if (mold == 1):
assert beta % 2 == 0
self.a,self.mold,self.alpha,self.beta=a,mold,alpha,beta
def cauchy(self,x):
'''
柯西型
:param x:
:param a: 绝对值开始/结束
:param mold:
:param alpha: 可以选1/sqrt(a)
:param beta: 变化速度 越大越快 1为线性
:return:
'''
a, mold, alpha, beta=self.a,self.mold,self.alpha,self.beta
f=lambda b:1/(1+alpha*(x-alpha)**b)
if(mold==1):
u=f(beta)
elif(mold==0):
if(x<=a):
u=1
else:
u=f(beta)
elif(mold==2):
if(x<=a):
u=0
else:
u=f(-beta)
else:
super().no_mold(mold)
return
return u
class Gamma(MembershipDegree):
def __init__(self,a,b=None,mold=0,k=2):
if (mold == 1):
assert b != None
self.a,self.b,self.mold,self.k=a,b,mold,k
def gamma(self,x):
'''
伽马型
:param x:
:param a:
:param b:
:param mold:
:param k:
:return:
'''
a, b, mold, k= self.a, self.b, self.mold, self.k
f=lambda :exp(-k*(x-a))
if(mold==1):
if(xb):
u=exp(-k*(x-b))
else:
u=1
elif(mold==0):
if(x<=a):
u=1
else:
u=f()
elif(mold==2):
if(x<=a):
u=0
else:
u=1-f()
else:
super().no_mold(mold)
return
return u
if __name__ == '__main__':
# 画图测试
x=np.arange(0,10,0.01)
# 实例化一个伽马
g=Gauss(a=3,mold=1)
# 用父类函数运算哈哈哈
y=g.y_array(g.gauss,x)
g.huahua(x,y)
# plt.savefig('test')
plt.show()
pass
科学的隶属度函数确定方法
因为还有期末考试,所以我做了个demo
隶属度函数的建立
——关于年老,年轻,不大不小的设计说明
隶属度函数是模糊控制的应用基础,正确构造隶属度函数是能否用好模糊控制的关键之一。隶属度函数的确定过程,本质上说应该是客观的,但每个人对于同一个模糊概念的认识理解又有差异,因此,隶属度函数的确定又带有主观性。
由于时间、精力所限,结合题目情况,是一个生活观念的判断,我选择了例证法。即预选了几个年龄1~100岁,设置了几个有确定值的选项,如年轻,比较年轻,不年轻。让朋友圈的人帮忙打分。因为告诉大家我在做大作业,所以亲朋好友比较配合,很有默契地选择了有规律答案,方便我做拟合。
基于获得的少量数据,加上我主观判断,我选择了高斯、柯西型函数等,调整了一下参数,比较粗糙,还望多多包涵。
old_or_young.py
'''
设计一个年老,很年轻,不老也不年轻模糊集的隶属度函数
'''
from matplotlib import pyplot as plt
import numpy as np
# 从上一个包中导入
import membership_function as mf
x=np.arange(0,100,0.05)
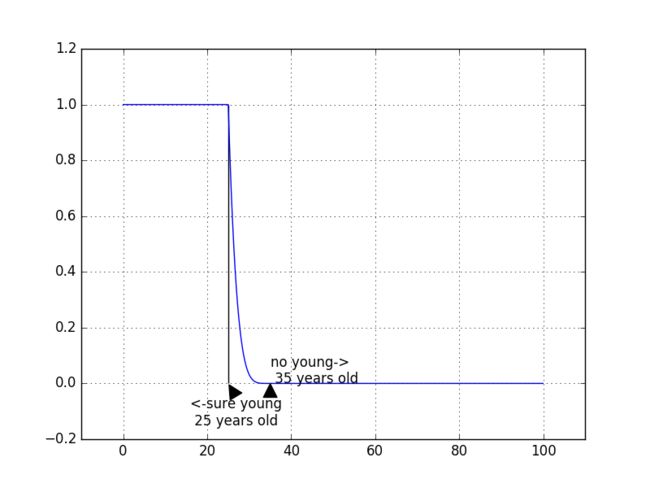
young=mf.Paracurve(a=25,b=35,k=5)
y=young.y_array(young.paracurve,x)
young.huahua(x,y)
plt.vlines(25,0,1,linestyles='-')
plt.annotate('<-sure young\n 25 years old',xy=(25,0),xytext=(16,-0.15),arrowprops = dict(facecolor = 'black', shrink = 0.1))
plt.annotate('no young->\n 35 years old',xy=(35,0),arrowprops = dict(facecolor = 'black', shrink = 0.1))
plt.savefig('young')
plt.show()
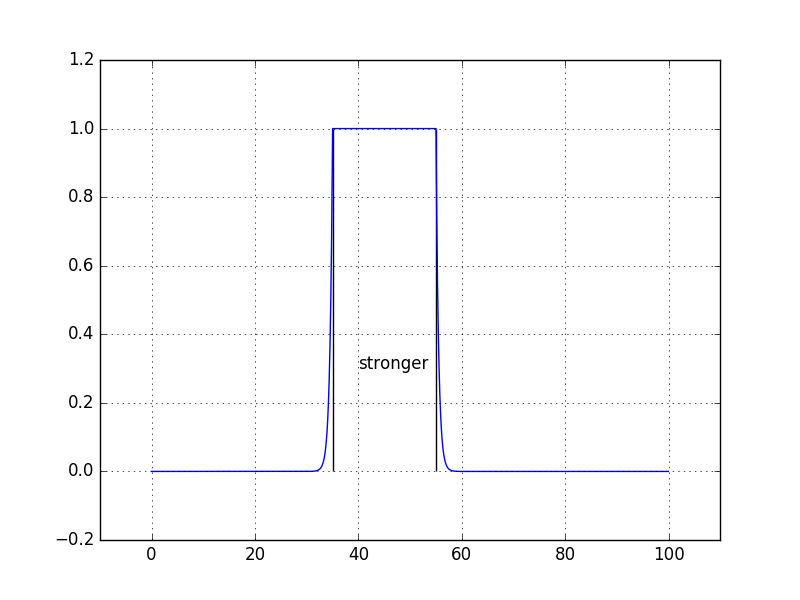
strong=mf.Gamma(35,55,1,k=2)
y=strong.y_array(strong.gamma,x)
strong.huahua(x,y)
plt.vlines(35,0,1,linestyles='-')
plt.vlines(55,0,1,linestyles='-')
plt.annotate('stronger',xy=(40,0.3))
plt.savefig('strong')
plt.show()
young=mf.Paracurve(a=50,b=65,mold=2,k=5)
y=young.y_array(young.paracurve,x)
young.huahua(x,y)
plt.vlines(65,0,1,linestyles='-')
plt.annotate('big age->\n 65 years old',xy=(65,0),arrowprops = dict(facecolor = 'black', shrink = 0.1))
plt.savefig('bigage')
plt.show()