运行要求
运行时间限制: 2sec
内存限制: 1024MB
题目
多叉树G拥有N个顶点。顶点编号从1到N,一次累加。多叉树的第i条树枝由顶点ai和顶点bi连接在一起。
现在考虑要在多叉树G的树枝上涂上颜色。这个时候对颜色有一个要求。就是从任意一个顶点出发,这个顶点所连接的边的颜色要求各自不同。
满足以上条件的的涂色方案里,所使用的颜色最少的方案是哪种方案。
要求
- 2<=N<=100000
- 1<=ai<=bi<=N
- 所有的输入都为整数
- 给定的图形是树结构
输入
输入都以以下标准从命令行输入
N
a1 b1
a2 b2
.
.
.
aN-1 bN-1输出
输出的行数为N行
第一行输出使用的颜色数量
第i+1行(1<=i<=N-1)输出用于表示第i条树枝颜色的ci。这里ci一定是满足1<=ci<=K。
满足条件的配色方案钟,使用最少颜色的涂色方案可能会有很多种,选择其中一种输出即可例1
输入
3
1 2
2 3输出
2
1
2例2
输入
8
1 2
2 3
2 4
2 5
4 7
5 6
6 8输出
4
1
2
3
4
1
1
2例3
输入
6
1 2
1 3
1 4
1 5
1 6输出
5
1
2
3
4
5解题思路
读懂题目
1. 多叉树上面有N个顶点。i为树枝的编号并且满足i<=N-1。
总结一下条件就是有N的顶点有N-1个树枝
2. 我们以例2为例子
8
1 2
2 3
2 4
2 5
4 7
5 6
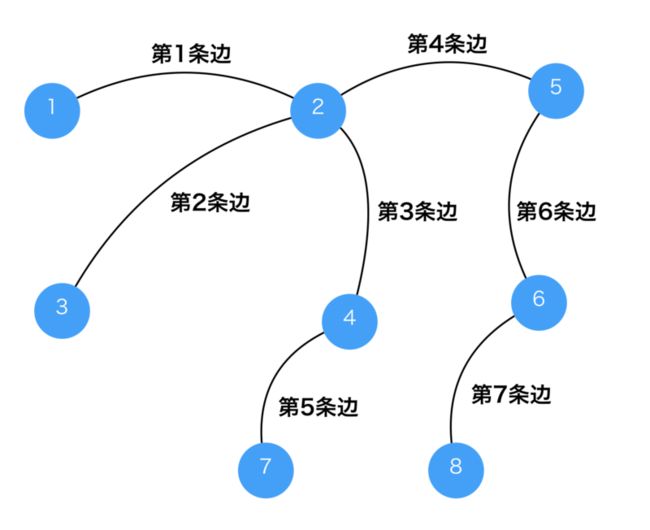
6 8N = 8,有8个点。我们依次编号为1,2,3,4,5,6,7,8。
第1条树枝为第1个点和第2个点的连线。
第2条树枝为第2个点和第3个点的连线。
第3条树枝为第2个点和第4个点的连线。
...
第7条树枝为第6个点和第8个点的连线。
3. 满足条件的涂色方案
如下图所示,所有的顶点所连接的树枝的颜色都是不一样的。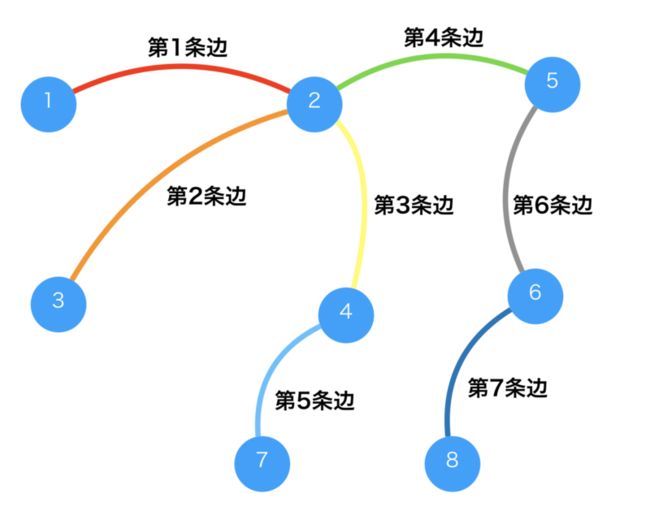
图2
4. 不满足条件的涂色方案
如下图所示,连接顶点2的两个树枝都为红色,不满足要求
图3
5. 如何满足最少的颜色
我们来试着优化图2
顶点2的连接树枝,第1条边,第2条边,第3条边,第4条边因为连接的是同一个顶点,所以颜色必须保持各个不一样。
第5条边,我们其实是可以用第1条边的红色
第6条边,我们也可以用第1条边的红色
第6条边用红色的话,第7条边的颜色为了和第6条边保持不一样,可以用现有的紫色,但是为了保持颜色数量成本,也可以用第2条边的橙色。
那么我们可以得出优化后的结果如图4所示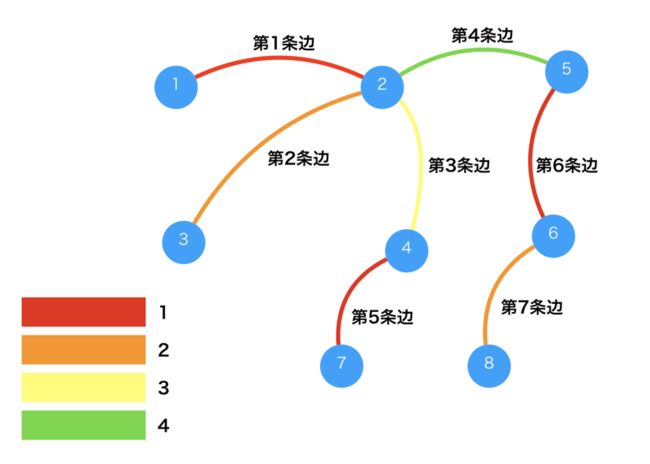
图4
我们再给各个颜色编上号
红色为1
橙色为2
黄色为3
绿色为4
按照第1条边到第7条边的顺序,我们可以得出
1,2,3,4,1,1,2的结果
解题思路
最少有多少种颜色
每个顶点所连接的树枝的颜色都需要不一样
树枝少的顶点可以从树枝多的顶点那里借颜色
如下图所示,顶点4和顶点5都为只有两个树枝的顶点,它们可以从有4个树枝的顶点2那儿借到红色。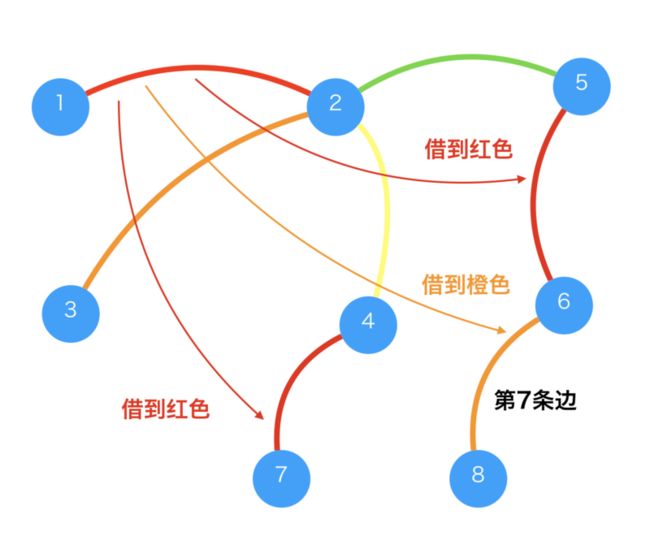
颜色其实可以抽象成为数字
而这些数字的排列可以看作从1开始的累加,只是相邻的顶点有别的标号为M的树枝的话,累加时要跳过M。
这里请看动图里面的skip。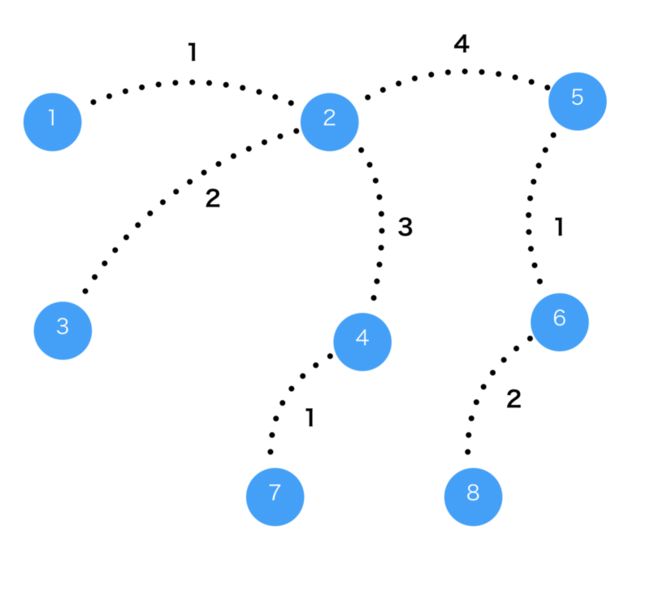
具体步骤
找到任意一顶点X开始做DFS遍历。遍历到顶点N的树枝的时候对顶点N的每个树枝做累加标记。如果这个顶点N是从M过来的,并且M到N的树枝的标记是X的话,那么在累加标记顶点N的树枝的时候,要跳过M。
最后
输出树枝最多的顶点的树枝数量
按照树枝的顺序,输出树枝的标记
动图
代码
from sys import setrecursionlimit
setrecursionlimit(100000)
n = int(input())
arr = []
for i in range(n-1):
S = input()
ar = [int(s) for s in S.split(" ")]
arr.append(ar)
def prepare(n, arr):
data = [[] for i in range(n)]
nodeStates = [-1 for i in range(n)]
childNums = [0 for i in range(n)]
for ar in arr:
start = ar[0] - 1
to = ar[1] - 1
data[start].append(to)
data[to].append(start)
return data, nodeStates, childNums
data, nodeStates, childNums = prepare(n, arr)
mmk = {}
def generateID(start,to):
if start < to:
start,to = to, start
return start * 100000 + to
def dfs(currentNode, arr, x):
childNodes = arr[currentNode]
nodeStates[currentNode] = 1
childNums[currentNode] = len(childNodes)
kk = 0
for ch in childNodes:
if nodeStates[ch] == -1:
kk = kk + 1
if kk == x:
kk = kk + 1
mmk[generateID(currentNode+1,ch+1)] = kk
dfs(ch, arr, kk)
dfs(0, data, -1)
print(max(childNums))
for ar in arr:
start = ar[0]
to = ar[1]
print(mmk[generateID(start,to)])
注意的地方
from sys import setrecursionlimit
setrecursionlimit(100000)这个要加上,不然会有run time error的报错
输出的时候根据树枝的两端顶点进行的编号,使用python的dictionary完成对于树枝信息的高速读取和输出