编者注:本文包含了使用Python2.X读取数据、数据处理、作图,构建梯度下降法函数求解一元线性回归,并对结果进行可视化展示,是非常综合的一篇文章,包含了Python的数据操作、可视化与机器学习等内容。学习了这一篇文章就大概了解或掌握相关Python编程与数据分析等内容。另外,本文还巧妙地进行了一个设计,这使得本文Python代码也可用于多元线性回归,这是区别与现有网络上大多数梯度下降法求解线性回归的Python实现不同,具体会在文中说明。
五、构造梯度下降法求解回归的函数
根据相关文献,梯度下降法的主要精髓在于梯度、下降,也就是计算损失函数的梯度,然后在初始值下不断下降,寻找迭代之后损失函数达到最小的数值。对于我们的函数J(θ)求偏导J:
下面是更新的过程,也就是θi会向着梯度最小的方向进行减少。θi表示更新之前的值,-后面的部分表示按梯度方向减少的量,α表示步长(学习率),也就是每次按照梯度减少的方向变化多少。
这一方法也称为批量梯度下降。其代码如下:
def gradientDescent(X, y, theta, alpha, iters):
temp = np.matrix(np.zeros(theta.shape)) #构建零值矩阵
parameters = int(theta.ravel().shape[1]) #计算需要求解的参数个数
cost = np.zeros(iters) #构建iters个0的数组
for i in range(iters):
error = (X * theta.T) – y #计算hθ(x)-y
for j in range(parameters):
term = np.multiply(error, X[:,j]) #计算两矩阵(hθ(x)-y)x
temp[0,j] = theta[0,j] - ((alpha / len(X)) * np.sum(term))
theta = temp
cost[i] = computeCost(X, y, theta)
return theta, cost
在这里alpha为学习率,iters为迭代次数。先构造一些零值矩阵或数组,然后再根据梯度下降法最后得到的计算公式来得到求解值theta,即temp[0,j] = theta[0,j] - ((alpha / len(X)) * np.sum(term)),中简掺杂一些矩阵的计算准备。
输入学习率、迭代次数等初始值,就可以得到求解回归的参数值。
alpha = 0.001
iters = 100000
theta = np.matrix(np.array([0,0]))
# perform gradient descent to "fit" the model parameters
g, cost = gradientDescent(X, y, theta, alpha, iters)
g
得到结果为:g=[12.0805357, 0.14831209]T,其最终损失函数值为:
···
computeCost(X, y, g)
···
结果为3.1228871926562922,在这里需要注意梯度下降法的结果与学习率、迭代次数等初始值设置有关,学习率太大会使得梯度下降幅度太大,有可能越过最小值,而太小了,又会使迭代过程变慢。迭代次数的设置也有可能使得最终结果没有落在损失函数最小的那一次结果上,因此在这里得到的梯度下降法,其损失函数值并未比最小二乘法优越多少。
六、梯度下降法求解结果的可视化
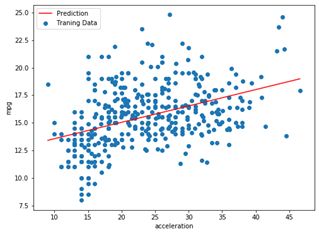
将梯度下降法得到的拟合曲线与(x,y)散点放在一起,展示结果拟合程度的可视化。分别用plot、scatter命令建立折线和散点,并使用fig, ax = plt.subplots(figsize=(8,6))将两图放在一起。
···
x = np.linspace(data.mpg.min(), data.mpg.max(), 100) #创建mpg数据的等差数列
f = g[0, 0] + (g[0, 1] * x #依据拟合方程创建f值
fig, ax = plt.subplots(figsize=(8,6))
ax.plot(x, f, 'r', label='Prediction')
ax.scatter(data.mpg, data.acceleration, label='Traning Data')
ax.legend(loc=2) #图例
ax.set_xlabel('acceleration')
ax.set_ylabel('mpg')
plt.show()
···
···
fig, bx = plt.subplots(figsize=(8,6))
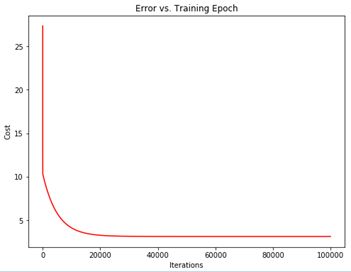
bx.plot(np.arange(iters), cost, 'r')
bx.set_xlabel('Iterations')
bx.set_ylabel('Cost')
bx.set_title('Error vs. Training Epoch')
plt.show()
··· 结果可以看出,最初的梯度下降很快,在20000次之后开始趋于平稳。
另外,要特别说明的是:本文所构建的梯度下降法求解函数也适用于多元线性回归,原因是本文在构建X、y变量时采用了矩阵化的处理,而不是像一般方法直接从数据中选择变量,另外,X、y变量的定位也没有固定在某几行,而是依据data的数值形状来定位,即这几行代码的设置:
cols = data.shape[1]
X = data.iloc[:,0:cols-1]
y = data.iloc[:,cols-1:cols]
完整代码地址:http://note.youdao.com/noteshare?id=4b0d35625b292621bdc8f31f31effa82
写作不易,特别是技术类的写作,请大家多多支持,关注、点赞、转发等等。
————————
参考文献:
- Machine Learning Exercises In Python, Part 1,
http://www.johnwittenauer.net/machine-learning-exercises-in-python-part-1/ - (吴恩达笔记 1-3)——损失函数及梯度下降
http://blog.csdn.net/wearge/article/details/77073142?locationNum=9&fps=1 - 梯度下降法求解线性回归之python实现
http://blog.csdn.net/just_do_it_123/article/details/51056260