实现一个正则表达式需要几步?
就三步:
- 分析正则表达式并构建出NFA
- 根据NFA得出DFA
- 根据DFA匹配字符串
当然,这只是最基本的,但是可以了解到正则表达式的实现原理,这篇文章实现三个最基本的正则操作: - 连接 abc 匹配 abc
- 或 ab|cd 匹配 ab或cd
- 重复 a* 匹配 任意多个a
(功能较完备的正则引擎:https://github.com/Qzhangqi/Regex)
第一步 (分析正则表达式并构建出NFA )
例子:ab(c|d)*
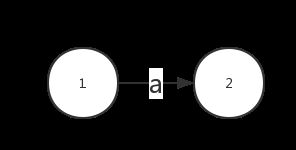
把正则中的每个字母都表示成两个节点用一条边相连,如表示 a
节点和图的数据结构
class Node {
int id; //节点的 id, 生成新节点时自动生成, 自增长
Map> nextNodes; //Character 表示边上的字符(转换条件)
boolean isEnd = false; //是否是结束节点
}
class Graph {
Node start; //图的开始节点
Node end; //图的结束节点
}
当读入一个a时这样处理
Node start = new Node();
Node end = new Node();
start.addNextNode('a', end);
graph = new Graph(start, end);
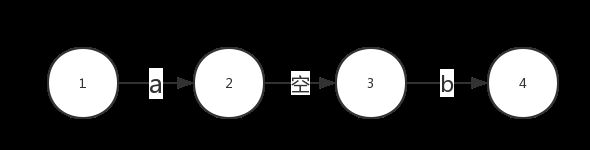
ab 两个字母首尾相连这样表示
Graph seriesGraph(Graph graph1, Graph graph2) {
graph1.end.addNextNode(' ', graph2.start);
graph1.end = graph2.end;
return graph1;
}
(c|d) 括号内的就整体处理和算术一样 | 号这样表示
void parallelGraph(Graph graph1, Graph graph2) {
Node start = new Node();
Node end = new Node();
start.addNextNode(' ', graph1.start);
start.addNextNode(' ', graph2.start);
graph1.end.addNextNode(' ', end);
graph2.end.addNextNode(' ', end);
graph1.start = start;
graph1.end = end;
}
(c|d)* *号加一条从尾到首的空转移
void repeatGraph(Graph graph) {
graph.end.addNextNode(' ', graph.start);
}
再把ab和(c|d)*连起来,最后结果是这样的
好了,这就一个NFA(非确定有限状态机)了, 你肯定也想到了,匹配字符串时就是将字符一个一个读入,然后根据读入的字符在 1 2 3 4 5 ....这些状态之间转换,然后判断是否到了结束状态就可以得出是否匹配成功,但是NFA和字符串进行匹配效率太低,原因有二:
- 空边无用,需要消除,空边是构造NFA时起辅助作用的,匹配时就不再需要了
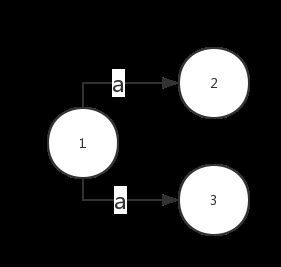
- 转移状态非确定,需要合并相同边,考虑这样一种情况:
这在读入 a 时是转换到 2 状态,还是 3 状态,如果随机进入一个状态,到后面不匹配还需要回溯,影响性能。
第二步(根据NFA得出DFA )
例子是一个这样的正则表达式:a(a|b|c)*cba,使用上一步的办法构造出来的NFA是这样的
当把它转换成一个DFA时,我们决定不用 Node 这样的数据结构来储存这张图了,而是用一张表
class StateTable {
State[][] stateTable; //状态表
Map mapx; //转换条件到数组横坐标的映射
// 当你要实现一个像 \w 这样的通配字符时,可以用整形储存转换条件,然后再加一个映射关系
Map mapy; //状态到数组纵坐标的映射
}
class State {
List id; //状态的 id, 状态将有多个 id
boolean isEnd; //是否是结束态
}
拿上图中的前四个点举个例
| a | b | c | 空 | |
|---|---|---|---|---|
| {0} | {9} | null | null | null |
| {9} | null | null | null | {7} |
| {7} | null | null | null | {1,3,5} |
| {1} | {2} | null | null | null |
开始转换了
先把表的列确定下来,在读入正则时根据不同的字符填充 mapx
| a | b | c |
|---|
然后对起始点 bfs 但是这里的 bfs 有点不一样,只有空边的下一个节点才会添加入 bfs 队列,而非空边的下一节点直接加入 stateTable 状态表,这样就消除了空边
ps:这里给出的代码都是伪代码,是帮助理解的,和真正程序里的代码是有区别的,比如没有记录一个 State 是否是结束状态,在实现时要注意
//startNode 起始点
void start(Node startNode) {
State state = new State();
state.nodes.add(startNode);
addline(state);
}
//添加一行
void addline(State state) {
for (Node node : state.nodes) {
bfs(node, state);
}
}
void bfs(Node snode, State state) {
ArrayList bfsNodes = new ArrayList<>(); // bfs队列
bfsNodes.add(snode);
while (!bfsNodes.isEmpty()) {
Node node = bfsNodes.remove(0);
for (int i : node.nextNodes.keySet()) {
for (Node node0 : node.nextNodes.get(i)) {
//上两行不用管,知道这里 node0 是 snode 的下一个节点
// i 是 snode 到 node0 的转换条件
if (!node0.look) {
node0.look = true;
if ((char)i != ' ')
// 列号 行号 状态id
stateTable.addState((char)i, state, node0.getId());
else
bfsNodes.add(node0);
}
}
}
}
}
处理完头节点,这个表就这样了
| a | b | c | |
|---|---|---|---|
| {0} | {9} | null | null |
把刚刚添加的这一行中所有的 State 添加进一个队列 (添加过的不重复添加),从队列中一个一个取出 State 进行处理,直到队列空
void start(Node startNode) {
State state = new State();
state.nodes.add(startNode);
ArrayList states = new ArrayList<>(); //状态队列
states.add(state);
while (!states.isEmpty()) {
State state1 = states.pollFirst();
addline(state1);
//这个函数会根据 state1(行号 mapy中映射成 y 坐标)
//去查 stateTable 将这一行中的所有状态添加进 states
//添加时还会和 stateTable 中的所有 行号 比较,有了的就不添加了
stateTable.add(state1, states);
}
}
完成后 stateTable 就是这个样子, 这就是 DFA (确定有限状态机)
第三步(根据DFA匹配字符串)
这步比较简单了,直接看代码
public boolean match(String matched) {
//头一行的行号
State state = stateTable.getFirstLine();
for (int i = 0; i < matched.length ; i++) {
char ch = matched.charAt(i);
//根据 行号 列号 获得状态
state = stateTable.get(state, ch);
}
return state.isEnd;
}