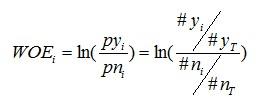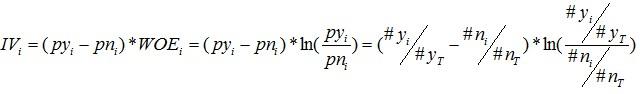互金公司信用评分卡建模
一、分析原理
信用评分卡模型在国外是一种成熟的预测方法,尤其在信用风险评估以及金融风险控制领域更是得到了比较广泛的使用,其原理是将模型变量WOE编码方式离散化之后运用logistic回归模型进行的一种二分类变量的广义线性模型。
二、分析背景
在互金公司的各种贷款业务中,普遍使用信用评分,根据客户的多个特征对每个客户进行打分,以期待对客户优质与否做一个评判。信用评分卡有三种:
A卡(Application scorecard), 即申请评分卡。用于贷款审批前期对借款申请人的量化评估;
B卡(Behavior scorecard),即行为评分卡。用于贷后管理,通过借款人的还款以及交易行为,结合其他维度的数据预测借款人未来的还款能力和意愿;
C卡(Collection scorecard),即催收评分卡。在借款人当前还款状态为逾期的情况下,预测未来该笔贷款变为坏账的概率。
三种评分卡根据使用时间不同,分别侧重贷前,贷中和贷后。本篇主要涉及A卡,即申请评分卡建模。在A卡中常用的有逻辑回归,AHP等,而在后面两种卡中,常使用多因素逻辑回归,精度等方面更好。
三、分析流程
1)数据读取:训练集数据、测试集数据
2)探索性分析EDA:变量分布情况-中位数、均值等
3)数据预处理:缺失值处理、异常值处理、特征相关性分析
4)特征选择:变量离散化、WOE变换
5)模型开发:逻辑回归
6)模型评估:K-S指标、拟合度曲线
7)信用评分:好坏比、基础分值等创立标准评分卡
8)对测试集进行预测和转化为信用评分卡
#导入包
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
import copy
from scipy import stats
from sklearn.ensemble import RandomForestRegressor
import warnings
warnings.filterwarnings('ignore')
1.数据读取及变量解释
每个变量的解释如下:
x0:SeriousDlqin2yrs:好坏客户
x1:RevolvingUtilization Of UnsecuredLines:无担保放款的循环利用:除了不动产和像车贷那样除以信用额度总和的无分期付款债务的信用卡和个人信用额度总额/可用额度比值
x2:Age:借款人年龄
x3:NumberOfTime30-59DaysPastDueNotWorse:30-59天逾期次数
x4:DebtRatio:负债比例
x5:MonthlyIncome:月收入
x6:Number Of OpenCreditLinesAndLoans:开放式信贷和贷款数量
x7:NumberOfTimes90DaysLate:90天逾期次数:借款者有90天或更高逾期的次数
x8:NumberReal Estate Loans Or Lines:不动产贷款或额度数量:抵押贷款和不动产放款包括房屋净值信贷额度
x9:Number Of Time 60-89Days PastDue Not Worse:60-89天逾期次数
x10:NumberOfDependents:家属数量,不包括本人在内的家属数量
#1)数据读取:训练集数据、测试集数据
train_data = pd.read_csv('/home/kesci/work/cs-training.csv')
test_data = pd.read_csv('/home/kesci/work/cs-test.csv')
train_data.head()
test_data.head()
#查看数据维度和信息
#训练集
print(train_data.shape)
print('-------------------')
print(train_data.info())
print('-------------------')
#测试集
print(test_data.shape)
print('-------------------')
print(test_data.info())
#可以看出月收入和家属数量有缺失值
我们通过观察了解到:
训练集和测试集的shape分别是(150000,12)和(101503,12),数据虽然维数不高,但是数据样本够大。
Unnamed:0 代表的是样本的序号,不是具体的特征,后面可将这一行所为索引;SeriousDlqin2yrs:1代表坏客户,0代表好客户,是这个项目的目标变量,我们根据训练集中的数据来预测测试集中SeriousDlqin2yrs的值。
剩下的10列特征是用户的个人信息,他们的不同值构成了不同的用户,我们主要根据这些特征来预测目标变量。
综上:这是一个十维特征构成的二分类问题。
2.数据探索分析
2.1 查看各特征数据的分布
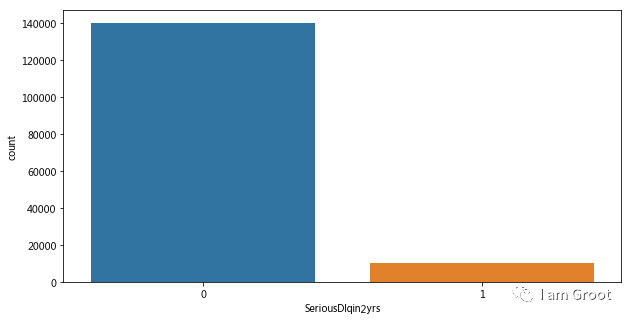
我们首先查看训练集中目标变量的分布信息,使用seaborn.countplot进行可视化。
好坏客户分布:我们可以看到样本中好坏客户的比例接近7:93,样本分布及其不均衡,我们在后面建模时需要注意。
#更改数据集索引
train_data.set_index('Unnamed: 0',inplace=True)
test_data.set_index('Unnamed: 0',inplace=True)
#2.1查看好坏客户分布
#创建子图及间隔设置
f,ax = plt.subplots(figsize=(10,5))
sns.countplot('SeriousDlqin2yrs',data=train_data)
plt.show()
badnum=train_data['SeriousDlqin2yrs'].sum()
goodnum=train_data['SeriousDlqin2yrs'].count()-train_data['SeriousDlqin2yrs'].sum()
print('训练集数据中,好客户数量为:%i,坏客户数量为:%i,坏客户所占比例为:%.2f%%' %(goodnum,badnum,(badnum/train_data['SeriousDlqin2yrs'].count())*100))
#样本标签及其不平衡,后面需要使用balance参数
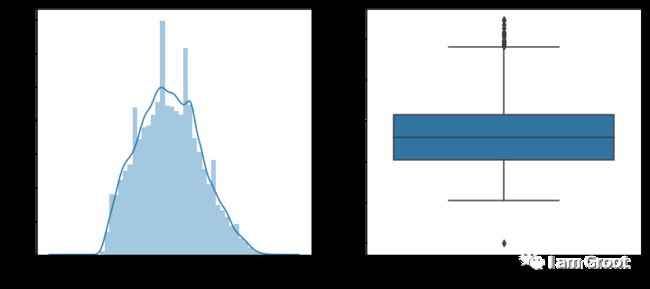
#2.2可用额度比值特征分布
f,[ax1,ax2]=plt.subplots(1,2,figsize=(12,5))
sns.distplot(train_data['RevolvingUtilizationOfUnsecuredLines'],ax=ax1)
sns.boxplot(y='RevolvingUtilizationOfUnsecuredLines',data=train_data,ax=ax2)
plt.show()
print(train_data['RevolvingUtilizationOfUnsecuredLines'].describe())
#我们使用seaborn.distplot和boxplot画出该特征分布,并且配合describe()查看数据的统计信息,数据分布及其不正常,中位数和四分之三位数都小于1,但是最大值确达到了50708,可用额度比值应该小于1,所以后面将大于1的值当做异常值剔除。
#2.3年龄分布
f,[ax1,ax2]=plt.subplots(1,2,figsize=(12,5))
sns.distplot(train_data['age'],ax=ax1)
sns.boxplot(y='age',data=train_data,ax=ax2)
plt.show()
print(train_data['age'].describe())
train_data[train_data['age']<18]#只有1条,而且年龄为0,后面当做异常值删除
train_data[train_data['age']>100]#较多且连续,可暂时保留
#2.4逾期30-59天 | 60-89天 | 90天笔数分布:
f,[[ax1,ax2],[ax3,ax4],[ax5,ax6]] = plt.subplots(3,2,figsize=(12,5))
sns.distplot(train_data['NumberOfTime30-59DaysPastDueNotWorse'],ax=ax1)
sns.boxplot(y='NumberOfTime30-59DaysPastDueNotWorse',data=train_data,ax=ax2)
sns.distplot(train_data['NumberOfTime60-89DaysPastDueNotWorse'],ax=ax3)
sns.boxplot(y='NumberOfTime60-89DaysPastDueNotWorse',data=train_data,ax=ax4)
sns.distplot(train_data['NumberOfTimes90DaysLate'],ax=ax5)
sns.boxplot(y='NumberOfTimes90DaysLate',data=train_data,ax=ax6)
plt.show()
print(train_data[train_data['NumberOfTime30-59DaysPastDueNotWorse']>13].count())
print('----------------------')
#这里可以看出逾期30-59天次数大于13次的有269条,大于80次的也是269条,说明这些是异常值,应该删除
print(train_data[train_data['NumberOfTime60-89DaysPastDueNotWorse']>13].count())
print('----------------------')
#这里可以看出逾期60-89天次数大于13次的有269条,大于80次的也是269条,说明这些是异常值,应该删除
print(train_data[train_data['NumberOfTimes90DaysLate']>17].count())
print('----------------------')
#这里可以看出逾期90天以上次数大于17次的有269条,大于80次的也是269条,说明这些是异常值,应该删除
#2.5负债率特征分布
f,[ax1,ax2] = plt.subplots(1,2,figsize=(12,5))
sns.distplot(train_data['DebtRatio'],ax=ax1)
sns.boxplot(y='DebtRatio',data=train_data,ax=ax2)
plt.show()
print(train_data['DebtRatio'].describe())
print('----------------------')
print(train_data[train_data['DebtRatio']>1].count())
#因为大于1的有三万多笔,所以猜测可能不是异常值
#2.6信贷数量特征分布
f,[ax1,ax2] = plt.subplots(1,2,figsize=(12,5))
sns.distplot(train_data['NumberOfOpenCreditLinesAndLoans'],ax=ax1)
sns.boxplot(y='NumberOfOpenCreditLinesAndLoans',data=train_data,ax=ax2)
plt.show()
print(train_data['NumberOfOpenCreditLinesAndLoans'].describe())
#由于箱型图的上界值挺连续,所以可能不是异常值
#2.7固定资产贷款数量
f,[ax1,ax2] = plt.subplots(1,2,figsize=(12,5))
sns.distplot(train_data['NumberRealEstateLoansOrLines'],ax=ax1)
sns.boxplot(y='NumberRealEstateLoansOrLines',data=train_data,ax=ax2)
plt.show()
print(train_data['NumberRealEstateLoansOrLines'].describe())
#查看箱型图发现最上方有异常值
print('----------------------')
print(train_data[train_data['NumberRealEstateLoansOrLines']>32].count())
#固定资产贷款数量大于28的有两个,大于32有一个为54,所以决定把>32的当做异常值剔除
#2.8家属数量分布
f,[ax1,ax2] = plt.subplots(1,2,figsize=(12,5))
sns.kdeplot(train_data['NumberOfDependents'],ax=ax1)
sns.boxplot(y='NumberOfDependents',data=train_data,ax=ax2)
plt.show()
print(train_data['NumberOfDependents'].describe())
print('----------------------')
print(train_data[train_data['NumberOfDependents']>15].count())
#由箱型图和描述性统计可以看出,20为异常值,可删除
#查看缺失比例
x=(train_data['SeriousDlqin2yrs'].count()-train_data['NumberOfDependents'].count())/train_data['SeriousDlqin2yrs'].count()
print('家属数量缺失比例为%.2f%%'%(x*100))
#缺失比例为2.6%,可直接删除
#2.9月收入分布
f,[ax1,ax2] = plt.subplots(1,2,figsize=(12,5))
sns.kdeplot(train_data['MonthlyIncome'],ax=ax1)
sns.boxplot(y='MonthlyIncome',data=train_data,ax=ax2)
plt.show()
print(train_data['MonthlyIncome'].describe())
print('----------------------')
print(train_data[train_data['MonthlyIncome']>2000000].count())
#查看缺失比例
x=(test_data['age'].count()-test_data['MonthlyIncome'].count())/test_data['age'].count()
print('月收入缺失数量比例为%.2f%%'%(x*100))
#由于月收入缺失数量过大,后面采用随机森林的方法填充缺失值
3.数据预处理
3.1 异常值处理
经过第二步数据探索分析,已经发现了一些变量里面的异常值,现在我们将其进行剔除
#3.1异常值处理
def strange_delete(data):
data=data[data['RevolvingUtilizationOfUnsecuredLines']<1]
data=data[data['age']>18]
data=data[data['NumberOfTime30-59DaysPastDueNotWorse']<80]
data=data[data['NumberOfTime60-89DaysPastDueNotWorse']<80]
data=data[data['NumberOfTimes90DaysLate']<80]
data=data[data['NumberRealEstateLoansOrLines']<50]
return data
train_data=strange_delete(train_data)
test_data=strange_delete(test_data)
#查看经过异常值处理后是否还存在异常值
train_data.loc[(train_data['RevolvingUtilizationOfUnsecuredLines']>1)|(train_data['age']<18)|(train_data['NumberOfTime30-59DaysPastDueNotWorse']>80)|(train_data['NumberOfTime60-89DaysPastDueNotWorse']>80)|(train_data['NumberOfTimes90DaysLate']>80)|(train_data['NumberRealEstateLoansOrLines']>50)]
test_data.loc[(test_data['RevolvingUtilizationOfUnsecuredLines']>1)|(test_data['age']<18)|(test_data['NumberOfTime30-59DaysPastDueNotWorse']>80)|(test_data['NumberOfTime60-89DaysPastDueNotWorse']>80)|(test_data['NumberOfTimes90DaysLate']>80)|(test_data['NumberRealEstateLoansOrLines']>50)]
print(train_data.shape)
print('----------------------')
print(test_data.shape)
#3.2缺失值处理
#3.2.1对家属数量的缺失值进行删除
train_data=train_data[train_data['NumberOfDependents'].notnull()]
print(train_data.shape)
print('----------------------')
test_data=test_data[test_data['NumberOfDependents'].notnull()]
print(test_data.shape)
#3.2缺失值处理
#3.2.2对月收入缺失值用随机森林的方法进行填充--训练集
#创建随机森林函数
def fillmonthlyincome(data):
known = data[data['MonthlyIncome'].notnull()]
unknown = data[data['MonthlyIncome'].isnull()]
x_train = known.iloc[:,[1,2,3,4,6,7,8,9,10]]
y_train = known.iloc[:,5]
x_test = unknown.iloc[:,[1,2,3,4,6,7,8,9,10]]
rfr = RandomForestRegressor(random_state=0,n_estimators=200,max_depth=3,n_jobs=-1)
pred_y = rfr.fit(x_train,y_train).predict(x_test)
return pred_y
#用随机森林填充训练集缺失值
predict_data=fillmonthlyincome(train_data)
train_data.loc[train_data['MonthlyIncome'].isnull(),'MonthlyIncome']=predict_data
print(train_data.info())
#3.2.2对月收入缺失值用随机森林的方法进行填充--测试集
#创建随机森林函数
def fillmonthlyincome(data):
known = data[data['MonthlyIncome'].notnull()]
unknown = data[data['MonthlyIncome'].isnull()]
x_train = known.iloc[:,[2,3,4,6,7,8,9,10]]
y_train = known.iloc[:,5]
x_test = unknown.iloc[:,[2,3,4,6,7,8,9,10]]
rfr = RandomForestRegressor(random_state=0,n_estimators=200,max_depth=3,n_jobs=-1)
pred_y = rfr.fit(x_train,y_train).predict(x_test)
return pred_y
#用随机森林填充测试集缺失值
predict_data=fillmonthlyincome(test_data)
test_data.loc[test_data['MonthlyIncome'].isnull(),'MonthlyIncome']=predict_data
print(test_data.info())
#缺失值和异常值处理完后进行检查
print(train_data.isnull().sum())
print('----------------------')
print(test_data.isnull().sum())
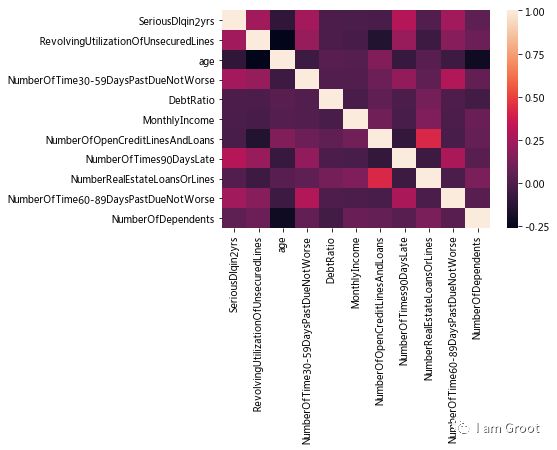
3.3 特征工程——特征共线性
1、特征间共线性:两个或多个特征包含了相似的信息,期间存在强烈的相关关系
2、常用判断标准:两个或两个以上的特征间的相关性系数高于0.8
3、共线性的影响:
1)降低运算效率
2)降低一些模型的稳定性
3)弱化一些模型的预测能力
4、查看共线性的方式:建立共线性表格或热力图
5、处理方式:删除或变换
#建立共线性表格
correlation_table = pd.DataFrame(train_data.corr())
#print(correlation_table)
#热力图
sns.heatmap(correlation_table)
#可以看到各个变量间的相关性都不大,所以无需剔除变量
4、特征选择
变量分为连续变量和分类变量。在评分卡建模中,变量分箱(binning)是对连续变量离散化(discretization)的一种称呼。要将logistic模型转换为标准评分卡的形式,这一环节是必须完成的。信用评分卡开发中一般有常用的等距分段、等深分段、最优分段。
单因子分析,用来检测各变量的预测强度,方法为WOE、IV;
这里使用IV值进行特征选择并且使用WOE对数据进行分箱。
1、WOE
WOE的全称是“Weight of Evidence”,即证据权重,WOE是对原始自变量的一种编码形式。
要对一个变量进行WOE编码,需要首先把这个变量进行分组处理(也叫离散化、分箱等等,说的都是一个意思)。分组后,对于第i组,WOE的计算公式如下:
其中,pyi是这个组中响应客户(风险模型中,对应的是违约客户,总之,指的是模型中预测变量取值为“是”或者说1的个体)占所有样本中所有响应客户的比例,pni是这个组中未响应客户占样本中所有未响应客户的比例,#yi是这个组中响应客户的数量,#ni是这个组中未响应客户的数量,#yT是样本中所有响应客户的数量,#nT是样本中所有未响应客户的数量。
从这个公式中我们可以体会到,WOE表示的实际上是“当前分组中响应客户占所有响应客户的比例”和“当前分组中没有响应的客户占所有没有响应的客户的比例”的差异。
2、IV
IV的全称是Information Value,中文意思是信息价值,或者信息量;用来衡量自变量的预测能力;类似的指标还有信息增益、基尼系数等等。
IV计算公式,对于分组i,会有一个对应的IV值,计算公式如下:
有了一个变量各分组的IV值,就可以计算整个变量的IV值,把各分组的IV相加,其中,n为变量分组个数。
#4.1分箱
#连续性变量--- 定义自动分箱函数---最优分箱
def mono_bin(Y, X, n=10):# X为待分箱的变量,Y为target变量,n为分箱数量
r = 0 #设定斯皮尔曼 初始值
badnum=Y.sum() #计算坏样本数
goodnum=Y.count()-badnum #计算好样本数
#下面这段就是分箱的核心 ,就是机器来选择指定最优的分箱节点,代替我们自己来设置
while np.abs(r) < 1:
d1 = pd.DataFrame({"X": X, "Y": Y, "Bucket": pd.qcut(X, n)})#用pd.qcut实现最优分箱,Bucket:将X分为n段,n由斯皮尔曼系数决定
d2 = d1.groupby('Bucket', as_index = True)# 按照分箱结果进行分组聚合
r, p = stats.spearmanr(d2.mean().X, d2.mean().Y)# 以斯皮尔曼系数作为分箱终止条件
n = n - 1
d3 = pd.DataFrame(d2.X.min(), columns = ['min'])
d3['min']=d2.min().X #箱体的左边界
d3['max'] = d2.max().X #箱体的右边界
d3['bad'] = d2.sum().Y #每个箱体中坏样本的数量
d3['total'] = d2.count().Y #每个箱体的总样本数
d3['rate'] = d2.mean().Y
print(d3['rate'])
print('----------------------')
d3['woe']=np.log((d3['bad']/badnum)/((d3['total'] - d3['bad'])/goodnum))# 计算每个箱体的woe值
d3['badattr'] = d3['bad']/badnum #每个箱体中坏样本所占坏样本总数的比例
d3['goodattr'] = (d3['total'] - d3['bad'])/goodnum # 每个箱体中好样本所占好样本总数的比例
iv = ((d3['badattr']-d3['goodattr'])*d3['woe']).sum() # 计算变量的iv值
d4 = (d3.sort_index(by = 'min')).reset_index(drop=True) # 对箱体从大到小进行排序
print('分箱结果:')
print(d4)
print('IV值为:')
print(iv)
woe=list(d4['woe'].round(3))
cut=[] # cut 存放箱段节点
cut.append(float('-inf')) # 在列表前加-inf
for i in range(1,n+1): # n是前面的分箱的分割数,所以分成n+1份
qua=X.quantile(i/(n+1)) #quantile 分为数 得到分箱的节点
cut.append(round(qua,4)) # 保留4位小数 #返回cut
cut.append(float('inf')) # 在列表后加 inf
return d4,iv,cut,woe
x1_d,x1_iv,x1_cut,x1_woe = mono_bin(train_data['SeriousDlqin2yrs'],train_data.RevolvingUtilizationOfUnsecuredLines)
x2_d,x2_iv,x2_cut,x2_woe = mono_bin(train_data['SeriousDlqin2yrs'],train_data.age)
x4_d,x4_iv,x4_cut,x4_woe = mono_bin(train_data['SeriousDlqin2yrs'],train_data.DebtRatio)
x5_d,x5_iv,x5_cut,x5_woe = mono_bin(train_data['SeriousDlqin2yrs'],train_data.MonthlyIncome)
#离散型变量-手动分箱
def self_bin(Y,X,cut):
badnum=Y.sum() # 坏用户数量
goodnum=Y.count()-badnum #好用户数量
d1 = pd.DataFrame({"X": X, "Y": Y, "Bucket": pd.cut(X, cut)})#建立个数据框 X-- 各个特征变量 , Y--用户好坏标签 , Bucket--各个分箱
d2 = d1.groupby('Bucket', as_index = True)# 按照分箱结果进行分组聚合
d3 = pd.DataFrame(d2.X.min(), columns = ['min']) # 添加 min 列 ,不用管里面的 d2.X.min()
d3['min']=d2.min().X
d3['max'] = d2.max().X
d3['bad'] = d2.sum().Y
d3['total'] = d2.count().Y
d3['rate'] = d2.mean().Y
d3['woe']=np.log((d3['bad']/badnum)/((d3['total'] - d3['bad'])/goodnum))# 计算每个箱体的woe值
d3['badattr'] = d3['bad']/badnum #每个箱体中坏样本所占坏样本总数的比例
d3['goodattr'] = (d3['total'] - d3['bad'])/goodnum # 每个箱体中好样本所占好样本总数的比例
iv = ((d3['badattr']-d3['goodattr'])*d3['woe']).sum() # 计算变量的iv值 # 计算变量的iv值
d4 = (d3.sort_index(by = 'min')).reset_index(drop=True) # 对箱体从大到小进行排序
woe=list(d4['woe'].round(3))
return d4,iv,woe
ninf = float('-inf')#负无穷大
pinf = float('inf')#正无穷大
cutx3 = [ninf, 0, 1, 3, 5, pinf]
cutx6 = [ninf, 1, 2, 3, 5, pinf]
cutx7 = [ninf, 0, 1, 3, 5, pinf]
cutx8 = [ninf, 0,1,2, 3, pinf]
cutx9 = [ninf, 0, 1, 3, pinf]
cutx10 = [ninf, 0, 1, 2, 3, 5, pinf]
dfx3,ivx3,woex3 = self_bin(train_data.SeriousDlqin2yrs,train_data['NumberOfTime30-59DaysPastDueNotWorse'], cutx3)
dfx6,ivx6 ,woex6= self_bin(train_data.SeriousDlqin2yrs, train_data['NumberOfOpenCreditLinesAndLoans'], cutx6)
dfx7,ivx7,woex7 = self_bin(train_data.SeriousDlqin2yrs, train_data['NumberOfTimes90DaysLate'], cutx7)
dfx8, ivx8,woex8 = self_bin(train_data.SeriousDlqin2yrs, train_data['NumberRealEstateLoansOrLines'], cutx8)
dfx9, ivx9,woex9 = self_bin(train_data.SeriousDlqin2yrs, train_data['NumberOfTime60-89DaysPastDueNotWorse'], cutx9)
dfx10,ivx10,woex10 = self_bin(train_data.SeriousDlqin2yrs, train_data['NumberOfDependents'], cutx10)
#4.2.1特征选择---相关系数矩阵
corr = train_data.corr()#计算各变量的相关性系数
xticks = ['x0','x1','x2','x3','x4','x5','x6','x7','x8','x9','x10']#x轴标签
yticks = list(corr.index)#y轴标签
fig = plt.figure(figsize=(10,8))
ax1 = fig.add_subplot(1, 1, 1)
sns.heatmap(corr, annot=True, cmap='rainbow', ax=ax1, annot_kws={'size': 12, 'weight': 'bold', 'color': 'black'})#绘制相关性系数热力图
ax1.set_xticklabels(xticks, rotation=0, fontsize=14)
ax1.set_yticklabels(yticks, rotation=0, fontsize=14)
plt.show()
#可见RevolvingUtilizationOfUnsecuredLines,NumberOfTime30-59DaysPastDueNotWorse,NumberOfTimes90DaysLate和NumberOfTime60-89DaysPastDueNotWorse这三个特征对于我们所要预测的值SeriousDlqin2yrs(因变量)有较强的相关性。
#相关性分析只是初步的检查,进一步检查模型的VI(证据权重)作为变量筛选的依据。
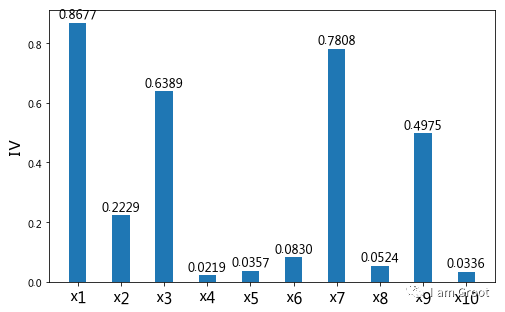
#4.2.2 IV值筛选
#通过IV值判断变量预测能力的标准是:小于 0.02: unpredictive;0.02 to 0.1: weak;0.1 to 0.3: medium; 0.3 to 0.5: strong
ivlist=[x1_iv,x2_iv,ivx3,x4_iv,x5_iv,ivx6,ivx7,ivx8,ivx9,ivx10]#各变量IV
index=['x1','x2','x3','x4','x5','x6','x7','x8','x9','x10']#x轴的标签
fig1 = plt.figure(1,figsize=(8,5))
ax1 = fig1.add_subplot(1, 1, 1)
x = np.arange(len(index))+1
ax1.bar(x,ivlist,width=.4) # ax1.bar(range(len(index)),ivlist, width=0.4)#生成柱状图 #ax1.bar(x,ivlist,width=.04)
ax1.set_xticks(x)
ax1.set_xticklabels(index, rotation=0, fontsize=15)
ax1.set_ylabel('IV', fontsize=16) #IV(Information Value),
#在柱状图上添加数字标签
for a, b in zip(x, ivlist):
plt.text(a, b + 0.01, '%.4f' % b, ha='center', va='bottom', fontsize=12)
plt.show()
'''
可以看出,DebtRatio (x4)、MonthlyIncome(x5)、NumberOfOpenCreditLinesAndLoans(x6)、NumberRealEstateLoansOrLines(x8)和NumberOfDependents(x10)变量的IV值明显较低,所以予以删除。
故选择特征:RevolvingUtilizationOfUnsecuredLines(x1)、age(x2)、NumberOfTime30-59DaysPastDueNotWorse(x3)、NumberOfTimes90DaysLate(x7)、NumberOfTime60-89DaysPastDueNotWorse(x9)作为后续评分模型建立的对象。
'''
5.建立模型
证据权重(Weight of Evidence,WOE)转换可以将Logistic回归模型转变为标准评分卡格式。引入WOE转换的目的并不是为了提高模型质量,只是一些变量不应该被纳入模型,这或者是因为它们不能增加模型值,或者是因为与其模型相关系数有关的误差较大,其实建立标准信用评分卡也可以不采用WOE转换。这种情况下,Logistic回归模型需要处理更大数量的自变量。尽管这样会增加建模程序的复杂性,但最终得到的评分卡都是一样的。
'''
5.1模型准备
在建立模型之前,我们需要将筛选后的变量转换为WoE值,便于信用评分
'''
#替换成woe函数
def trans_woe(var,var_name,woe,cut):
woe_name=var_name+'_woe'
for i in range(len(woe)): # len(woe) 得到woe里 有多少个数值
if i==0:
var.loc[(var[var_name]<=cut[i+1]),woe_name]=woe[i] #将woe的值按 cut分箱的下节点,顺序赋值给var的woe_name 列 ,分箱的第一段
elif (i>0) and (i<=len(woe)-2):
var.loc[((var[var_name]>cut[i])&(var[var_name]<=cut[i+1])),woe_name]=woe[i] # 中间的分箱区间 ,,数手指头就很清楚了
else:
var.loc[(var[var_name]>cut[len(woe)-1]),woe_name]=woe[len(woe)-1] # 大于最后一个分箱区间的 上限值,最后一个值是正无穷
return var
x1_name='RevolvingUtilizationOfUnsecuredLines'
x2_name='age'
x3_name='NumberOfTime30-59DaysPastDueNotWorse'
x7_name='NumberOfTimes90DaysLate'
x9_name='NumberOfTime60-89DaysPastDueNotWorse'
train_data=trans_woe(train_data,x1_name,x1_woe,x1_cut)
train_data=trans_woe(train_data,x2_name,x2_woe,x2_cut)
train_data=trans_woe(train_data,x3_name,woex3,cutx3)
train_data=trans_woe(train_data,x7_name,woex7,cutx7)
train_data=trans_woe(train_data,x9_name,woex9,cutx9)
Y=train_data['SeriousDlqin2yrs'] #因变量
#自变量,剔除对因变量影响不明显的变量
X=train_data.drop(['SeriousDlqin2yrs','DebtRatio','MonthlyIncome', 'NumberOfOpenCreditLinesAndLoans','NumberRealEstateLoansOrLines','NumberOfDependents'],axis=1)
X=train_data.iloc[:,-5:]
X.head()
#5.2 STATSMODEL包来建立逻辑回归模型得到回归系数,后面可用于建立标准评分卡
import statsmodels.api as sm
X1=sm.add_constant(X)
logit=sm.Logit(Y,X1)
result=logit.fit()
print(result)
print(result.summary())
6.模型评估
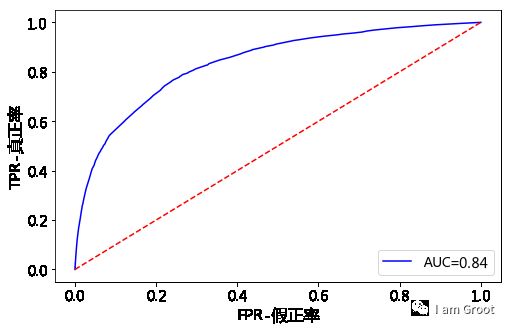
我们需要验证一下模型的预测能力如何。我们使用在建模开始阶段预留的test数据进行检验。通过ROC曲线和AUC来评估模型的拟合能力。在Python中,可以利用sklearn.metrics,它能方便比较两个分类器,自动计算ROC和AUC
#对训练集模型做模拟和评估
import statsmodels.api as sm
train_data=trans_woe(train_data,x1_name,x1_woe,x1_cut)
train_data=trans_woe(train_data,x2_name,x2_woe,x2_cut)
train_data=trans_woe(train_data,x3_name,woex3,cutx3)
train_data=trans_woe(train_data,x7_name,woex7,cutx7)
train_data=trans_woe(train_data,x9_name,woex9,cutx9)
#print(train_data)
#构建测试集的特征和标签
test_X=train_data.iloc[:,-5:] #测试数据 特征
#print(test_X)
test_Y=train_data.iloc[:,0]#测试数据 标签
#print(test_Y)
#print(test_Y.dtype)
#print(test_Y.count())
#评估
from sklearn import metrics
X3=sm.add_constant(test_X)
resu = result.predict(X3) #进行预测
fpr,tpr,threshold=metrics.roc_curve(test_Y,resu) #评估算法
rocauc=metrics.auc(fpr,tpr) #计算AUC
plt.figure(figsize=(8,5)) #只能在这里面设置
plt.plot(fpr,tpr,'b',label='AUC=%0.2f'% rocauc)
plt.legend(loc='lower right',fontsize=14)
plt.plot([0.0, 1.0], [0.0, 1.0], 'r--')
plt.xlim=([0.0, 1.0])
plt.ylim=([0.0, 1.0])
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.ylabel('TPR-真正率',fontsize=16)
plt.xlabel('FPR-假正率',fontsize=16)
plt.show()
从上图可知,AUC值为0.84,说明该模型的预测效果还是不错的,正确率较高
7.创建信用评分卡
在建立标准评分卡之前,还需要设定几个评分卡参数:基础分值、 PDO(比率翻倍的分值)和好坏比。 这里, 我们取600分为基础分值b,取20为PDO (每高20分好坏比翻一倍),好坏比O取20。
p=20/np.log(2)#比例因子
q=600-20*np.log(20)/np.log(2)#等于offset,偏移量
x_coe=[-2.7340,0.6526,0.5201,0.5581,0.5943,0.4329]#回归系数 ???
baseScore=round(q+p*x_coe[0],0)
#个人总评分=基础分+各部分得分
def get_score(coe,woe,factor):
scores=[]
for w in woe:
score=round(coe*w*factor,0)
scores.append(score)
return scores
#每一项得分
x1_score=get_score(x_coe[1],x1_woe,p)
x2_score=get_score(x_coe[2],x2_woe,p)
x3_score=get_score(x_coe[3],woex3,p)
x7_score=get_score(x_coe[4],woex7,p)
x9_score=get_score(x_coe[5],woex9,p)
def compute_score(series,cut,score):
list = []
i = 0
while i < len(series):
#print(series[i].dtype)
#print(series.iloc[i])
value = series.iloc[i]
j = len(cut) - 2
m = len(cut) - 2
while j >= 0:
if value >= cut[j]:
j = -1
else:
j -= 1
m -= 1
list.append(score[m])
i += 1
return list
train_data['BaseScore']=np.zeros(len(train_data))+baseScore
train_data['x1'] =compute_score(train_data['RevolvingUtilizationOfUnsecuredLines'], x1_cut, x1_score)
train_data['x2'] = compute_score(train_data['age'], x2_cut, x2_score)
train_data['x3'] = compute_score(train_data['NumberOfTime30-59DaysPastDueNotWorse'], cutx3, x3_score)
train_data['x7'] = compute_score(train_data['NumberOfTimes90DaysLate'], cutx7, x7_score)
train_data['x9'] = compute_score(train_data['NumberOfTime60-89DaysPastDueNotWorse'],cutx9,x9_score)
train_data['Score'] = train_data['x1'] + train_data['x2'] + train_data['x3'] + train_data['x7'] +train_data['x9'] + baseScore
scoretable1=train_data.iloc[:,[0,-7,-6,-5,-4,-3,-2,-1]] #选取需要的列,就是评分列
scoretable1.head()
colNameDict={'x1': 'RevolvingUtilizationOfUnsecuredLines' ,'x2':'age','x3':'NumberOfTime30-59DaysPastDueNotWorse',
'x7':'NumberOfTimes90DaysLate', 'x9':'NumberOfTime60-89DaysPastDueNotWorse'}
scoretable1=scoretable1.rename(columns=colNameDict,inplace=False)
scoretable1.to_excel(r'C:\Users\Administrator\Desktop\训练集评分卡.xlsx')
8.对测试集进行预测和转化为信用评分卡
#Logistic回归模型——将训练集的数据分为测试集和训练集
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
#自变量,剔除对因变量影响不明显的变量
train_data=train_data.drop(['DebtRatio','MonthlyIncome', 'NumberOfOpenCreditLinesAndLoans','NumberRealEstateLoansOrLines','NumberOfDependents'],axis=1)
training,testing=train_test_split(train_data,test_size=0.25,random_state=1)
#Y=train_data['SeriousDlqin2yrs'] #因变量
#X=train_data.iloc[:,-5:]
#创建训练集和测试集各自的自变量和因变量
x_train=training.iloc[:,-5:]
y_train=training['SeriousDlqin2yrs']
x_test=testing.iloc[:,-5:]
y_test=testing['SeriousDlqin2yrs']
clf = LogisticRegression()
clf.fit(x_train,y_train)
#对测试集做预测
score_proba = clf.predict_proba(x_test)
y_predproba=score_proba[:,1]
coe = clf.coef_
print(coe)
#对模型做评估
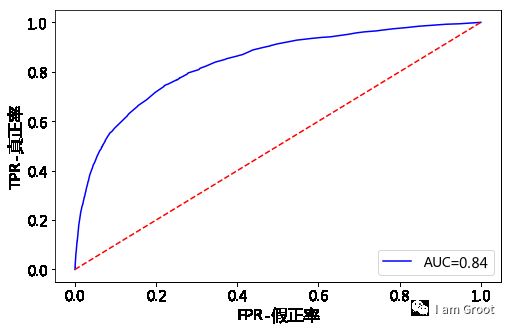
from sklearn.metrics import roc_curve,auc
fpr,tpr,threshold = roc_curve(y_test,y_predproba)
auc_score=auc(fpr,tpr)
plt.figure(figsize=(8,5)) #只能在这里面设置
plt.plot(fpr,tpr,'b',label='AUC=%0.2f'% auc_score)
plt.legend(loc='lower right',fontsize=14)
plt.plot([0, 1], [0, 1], 'r--')
plt.xlim=([0, 1])
plt.ylim=([0, 1])
plt.xticks(fontsize=14)
plt.yticks(fontsize=14)
plt.ylabel('TPR-真正率',fontsize=16)
plt.xlabel('FPR-假正率',fontsize=16)
plt.show()
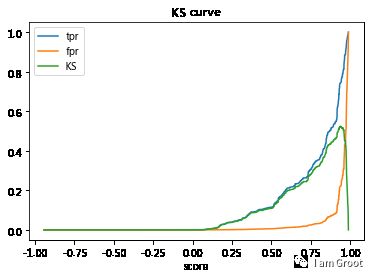
KS指标: 用以评估模型对好、坏客户的判别区分能力,计算累计坏客户与累计好客户百分比的最大差距。KS值范围在0%-100%,判别标准如下:
KS: <20% : 差
KS: 20%-40% : 一般
KS: 41%-50% : 好
KS: 51%-75% : 非常好
KS: >75% : 过高,需要谨慎的验证模型
fig,ax = plt.subplots()
ax.plot(1-threshold,tpr,label='tpr')
ax.plot(1-threshold,fpr,label='fpr')
ax.plot(1-threshold,tpr-fpr,label='KS')
plt.xlabel('score')
plt.title('KS curve')
plt.xlim=([0.0,1.0])
plt.ylim=([0.0,1.0])
plt.figure(figsize=(20,20))
legend=ax.legend(loc='upper left')
plt.show()
max(tpr-fpr)
#模型的AUC值达到0.84,K-S值达到0.525说明建模的效果很不错。
#预测测试集
#测试集转化为WOE值
test_data=trans_woe(test_data,x1_name,x1_woe,x1_cut)
test_data=trans_woe(test_data,x2_name,x2_woe,x2_cut)
test_data=trans_woe(test_data,x3_name,woex3,cutx3)
test_data=trans_woe(test_data,x7_name,woex7,cutx7)
test_data=trans_woe(test_data,x9_name,woex9,cutx9)
#自变量,剔除对因变量影响不明显的变量
test_data=test_data.drop(['DebtRatio','MonthlyIncome', 'NumberOfOpenCreditLinesAndLoans','NumberRealEstateLoansOrLines','NumberOfDependents'],axis=1)
X_test=test_data.iloc[:,-5:]
Y_test=test_data['SeriousDlqin2yrs'] #因变量
X_train=training.copy().iloc[:,-5:]
Y_train=training.copy()['SeriousDlqin2yrs']
clf = LogisticRegression()
clf.fit(X_train,Y_train)
#对测试集做预测
score_proba = clf.predict_proba(X_test)
#print(score_proba)
test_data['y_predproba']=score_proba[:,1]
#y_predproba = score_proba[:,1]
coe = clf.coef_
print('-------------------')
print(coe)
p=20/np.log(2)#比例因子
q=600-20*np.log(20)/np.log(2)#等于offset,偏移量
x_coe=[-2.7340,0.6526,0.5201,0.5581,0.5943,0.4329]#回归系数 ???
baseScore=round(q+p*x_coe[0],0)
#个人总评分=基础分+各部分得分
def get_score(coe,woe,factor):
scores=[]
for w in woe:
score=round(coe*w*factor,0)
scores.append(score)
return scores
#每一项得分
x1_score=get_score(x_coe[1],x1_woe,p)
x2_score=get_score(x_coe[2],x2_woe,p)
x3_score=get_score(x_coe[3],woex3,p)
x7_score=get_score(x_coe[4],woex7,p)
x9_score=get_score(x_coe[5],woex9,p)
def compute_score(series,cut,score):
list = []
i = 0
while i < len(series):
#print(series[i].dtype)
#print(series.iloc[i])
value = series.iloc[i]
j = len(cut) - 2
m = len(cut) - 2
while j >= 0:
if value >= cut[j]:
j = -1
else:
j -= 1
m -= 1
list.append(score[m])
i += 1
return list
test_data['BaseScore']=np.zeros(len(test_data))+baseScore
test_data['x1'] =compute_score(test_data['RevolvingUtilizationOfUnsecuredLines'], x1_cut, x1_score)
test_data['x2'] = compute_score(test_data['age'], x2_cut, x2_score)
test_data['x3'] = compute_score(test_data['NumberOfTime30-59DaysPastDueNotWorse'], cutx3, x3_score)
test_data['x7'] = compute_score(test_data['NumberOfTimes90DaysLate'], cutx7, x7_score)
test_data['x9'] = compute_score(test_data['NumberOfTime60-89DaysPastDueNotWorse'],cutx9,x9_score)
test_data['Score'] = test_data['x1'] + test_data['x2'] + test_data['x3'] + test_data['x7'] +test_data['x9'] + baseScore
scoretable2=test_data.iloc[:,[0,-8,-7,-6,-5,-4,-3,-2,-1]] #选取需要的列,就是评分列
print(scoretable2.head())
colNameDict={'x1': 'RevolvingUtilizationOfUnsecuredLines' ,'x2':'age','x3':'NumberOfTime30-59DaysPastDueNotWorse',
'x7':'NumberOfTimes90DaysLate', 'x9':'NumberOfTime60-89DaysPastDueNotWorse'}
scoretable2=scoretable2.rename(columns=colNameDict,inplace=False)
scoretable2.to_excel(r'C:\Users\Administrator\Desktop\测试集评分卡.xlsx')
#导出数据后再根据y_predproba<0.5的,SeriousDlqin2yrs=0,否则为1去填充
以上便是此次建模的全过程,欢迎指正~
参考资料:https://zhuanlan.zhihu.com/p/44663658