1. Error State EKF
ES-EKF是EKF的一种变种,它的基本思想就是把State区分为两部分:Nominal State和Error State。如下所示:
$$ x = \hat{x} + \delta x $$
其中$x$是True State,$\hat{x}$是Nominal State,$\delta x$是Error State。
ES-EKF直接估计Error State,然后用它矫正Nominal State。在整个滤波过程中,我们实际上修正的变量是$\delta x$,这点一定要清楚!!
Predection
$$ \begin{aligned} \underbrace{x_{k} - f(\hat{x}_{k-1}, u_k, 0)}_{\delta k} = F_k(\underbrace{x_{k-1} - \hat{x}_{k-1}}_{\delta_{k-1}}) + L_kw_{k} \\ \end{aligned} $$
$$ \Downarrow $$
$$ \delta_k=F_k\delta_{k-1} + L_k w_k $$
Measurement Update
$$ \begin{aligned} y_{k} = & h( \check{x}_k, 0) + H_k (\underbrace{x_k - \check{x}_k}_{\delta x_k}) + M_k v_k \end{aligned} $$
$$ \Downarrow $$
$$ \begin{aligned} y_{k} = & h( \check{x}_k, 0) + H_k {\delta x_k} + M_k v_k \end{aligned} $$
2.Error State Extended Kalman Filter的执行流程
1、Update Nominal State With Motion Model
$$ \check{x}_k = f({x}_{k-1}, u_k, 0) $$
注意,公式中的$x_{k-1}$是当前能获取的最优的State的估计值。可能是前一次Prediction产生的State值(连续多次使用Motion Model),也可能是Measurement Update后State值。
2、Propagete Uncertainty
$$ \check{P}_k = F_k {P}_{k-1} F_k^T + L_k Q_k L_k^T $$
同样的,在更新不确定性的过程中,需要根据所使用的state不同使用不同的$P_{k-1}$, Prediction阶段产生的State使用Motion Model的$P_{k-1}$,Measurement Update阶段产生的State使用测量阶段的$P_{k-1}$.
在接收到其它传感器的测量结果进行Measurement Update之前,步骤1)和步骤2)可以不断循环执行。
3、If A Measurement Available
3.1 Compute Kalman Gain
$$ K_k = \check{P}_k H_k^T(H_k \check{P}_kH_k^T + M_k R_k M_k^T)^{-1} $$
3.2 Computer Error State
$$ \delta\hat{x}_k = K_k (y_k - h_k(\check{x}_k,0)) $$
$$ \hat{P}_k = (1 - K_k H_k) \check{P}_k $$
3.3 Correct Nominal State
$$ \hat{x}_k = \check{x}_k + \delta \hat{x}_{k} $$
3.Error State Extended Kalman Filter的典型应用场景
在自动驾驶系统,主流的定位方案往往采用多传感器融合的定位方案,其中IMU(惯性测量单元)由于无须依赖外部信号,并且具有更高的更新频率,因此成为自动驾驶的标配传感器.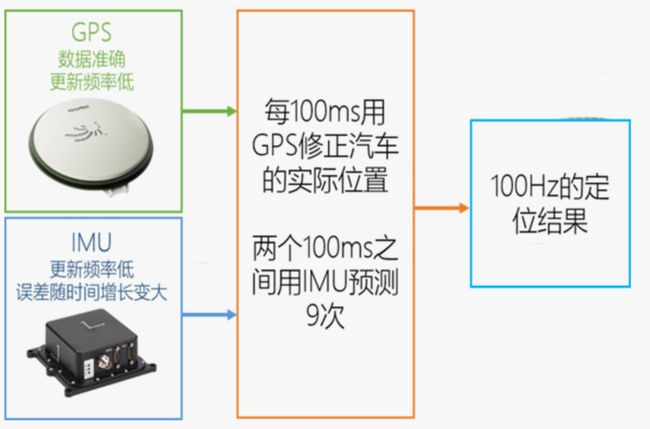
IMU的航迹推演(dead-reckoning)随着时间的推移,误差不断累积,为了避免定位位置出现偏移,需要每隔一段时间,都需要将IMU信息与GPS测量信息或者视觉定位信息进行融合.ES-EKF就是融合这些多传感器信息的有效方法之一.
4.Error State Extended Kalman Filter的优势
1.The orientation error-state is minimal (i.e., it has the same number of parameters as
degrees of freedom), avoiding issues related to over-parametrization (or redundancy)
and the consequent risk of singularity of the involved covariances matrices, resulting
typically from enforcing constraints.
2.The error-state system is always operating close to the origin, and therefore far from
possible parameter singularities, gimbal lock issues, or the like, providing a guarantee
that the linearization validity holds at all times.
3.The error-state is always small, meaning that all second-order products are negligible.
This makes the computation of Jacobians very easy and fast. Some Jacobians may
even be constant or equal to available state magnitudes.
4.The error dynamics are slow because all the large-signal dynamics have been integrated in the nominal-state. This means that we can apply KF corrections (which
are the only means to observe the errors) at a lower rate than the predictions.
参考链接
1.Quaternion kinematics for the error-state Kalman filter
2.Madyastha, Venkatesh, et al. "Extended Kalman filter vs. error state Kalman filter for aircraft attitude estimation." AIAA Guidance, Navigation, and Control Conference. 2011.
相关文章
自动驾驶定位系统-扩展卡尔曼滤波Extend Kalman Filter
自动驾驶系统定位与状态估计- Recursive Least Squares Estimation
自动驾驶系统定位与状态估计- Weighted Least Square Method
自动驾驶定位系统-State Estimation & Localization
个人网站地址: http://www.banbeichadexiaojiu...
