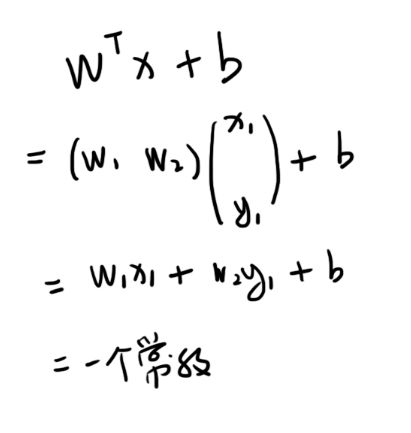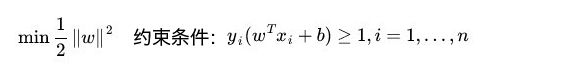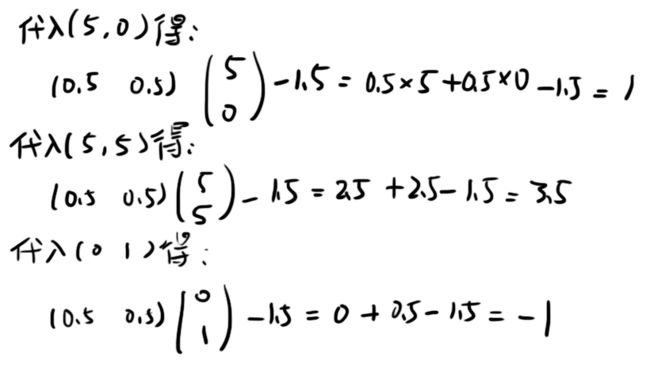写在前面
支持向量机是比较不容易理解的,网上有很多很详尽的技术文档,包括数学推导也写得颇为全面,奈何我就是怎么看也看不懂。经过多方面学习,虽然我现在也还是不很懂,特别是数学推导没有理解,但是我意识到其实根本没有关系,你只要能看懂结论里的公式就可以了。我用尽量简单的语言把基本过程说清楚。假设你和最早的我一样,什么也不懂,我们开始:
不过等等,为了帮助你理解,我还是推荐一个很详细的文档给你们:支持向量机通俗导论(理解SVM的三层境界)
还有一个视频:支持向量机在SPSS中
支持向量机
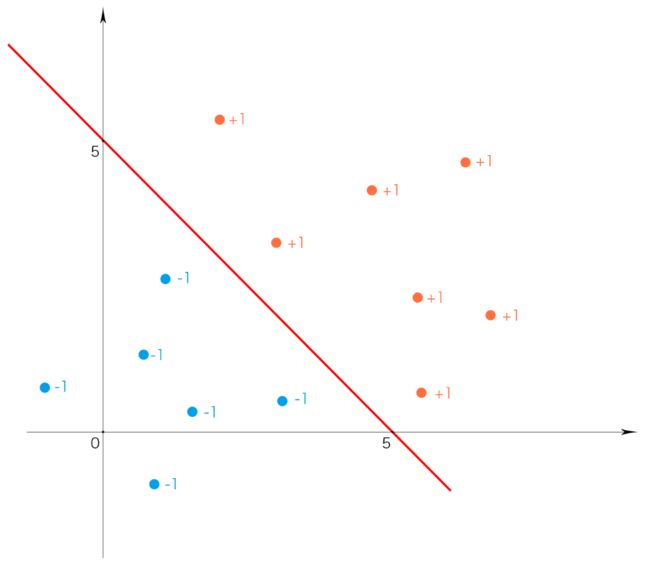
今天只说最简单的。你就将其理解为现在有很多点,一部分的标签是+1,一部分的标签是-1,而且这些点一定能被一条直线划分成两部分,我们的任务是“画一条线”把不同标签的数据分开。如下图所示:
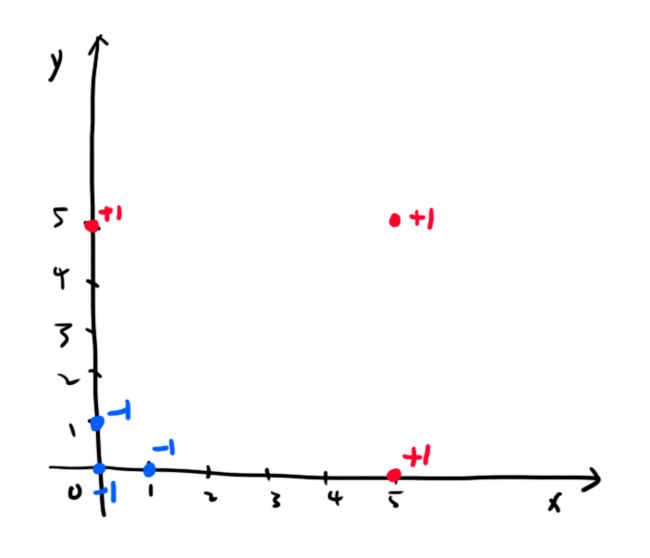
中间那条关键的线我们叫它超平面。是的没错,虽然它是一条直线,但我们还是叫它“超平面”。我们现在处理的是二维平面数据,此时超平面为一条直线。当我们处理的是三维空间数据时,超平面就是一个平面。而当我们处理的是100维数据时,超平面就是一个99维的对象。
所有资料都将这个超平面描述为:
千万不要认为他就是这条直线的方程式!不是这样的。wTx+b的结果其实是个分类标签,我们称 wTx+b 为分类器。假设右边橘红色的点标签都是+1,左边蓝色的点都是-1,那么当我们把具体的数据点,也就是这个具体数据点的(x, y)坐标带入wTx+b以后,输出的结果大于+1标签就是+1,小于-1标签就是-1。比如你输入(5, 5)这个点,带入 wTx+b 可能得出+2.5,那他的标签就是+1。(为什么是大于+1、小于-1而不是大于0、小于0我们之后讲。)从这里你也看到,本文wTx+b 中的 “x” 并不是一个数,而是一对数,是(5, 5)。所以 wTx+b 中的 wT 就是一个向量,计算的时候应该是这样的:
所以,只要我们找到向量wT和常数b,分类器就找到了,就能预测其他的数据点了。不过这里有个问题,那就是我们可以画出许多“超平面”,比如:
再比如:
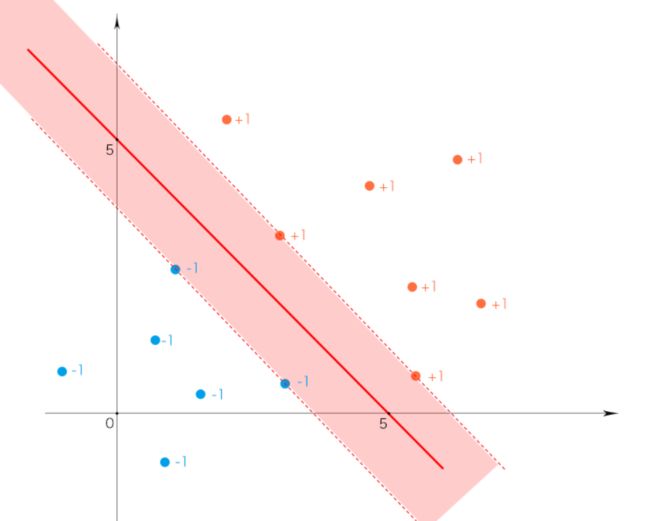
那么那一个“超平面”更好呢?我们认为第一个最好,因为它的“最大间隔”是最大的。
中间的超平面是wTx+b=0。这个很好理解,就是标签既不是+1,也不是-1。边界两条直线,右边是wTx+b=+1,左边是wTx+b=-1。这样有一个好处,就是如果你的数据点带入wTx+b算出来等于+1或者-1,那么说明这个数据点刚好在边界上,我们叫这样的点为“支持向量”。这里回答我们之前的那个问题,为什么输出结果是大于+1、小于-1而不是大于0、小于0,因为当等于+1或-1时可判断为支持向量,当大于-1小于1时,我们认为这个点处于间隔之内。这个值的绝对值越大,就越远离支持向量。
所以现在,换句话说,我们要找到“最大间隔”下的 wT 和 b。这个“间隔”如何求呢?我给你一个公式:
分母是w的二阶范数。
不要问我这个公式怎么来的,因为我也不知道。我可以给你再贴一张图,是我从《机器学习实战》这本书上截下来的,也许你能看懂(顺手强烈推荐这本书,真的非常好):
想要这个间距最大,那就要让分母最小。这里做了个等量代换,把求||x||的最小值转变为求0.5||x||^2的最小值。(也不要问我为什么是等价的。)当然这里是有约束条件的,就是所有你训练的点都必须在边界以外,用数学来表示是这样的:
所以现在我们是要在约束条件下求解,这个叫凸优化问题,因为现在的目标函数是二次的,约束条件是线性的,所以它是一个凸二次规划问题。这个在数学上有自己的方法求解,是这样的:
这是一个可编程的式子。
每一个数据点都对应一个 alpha ,alpha_i 和 alpha_j 表明,求最值需要alpha结对计算。话不多说,上代码。先给3个辅助函数:
# coding=utf-8
from numpy import *
# 载入数据,对txt文件解析
def loadDataSet(fileName):
dataMat = []
labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr = line.strip().split('\t')
dataMat.append([float(lineArr[0]), float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat, labelMat
# i是alpha的下标,m是所有alpha的数目
# 只要函数值不等于输入值i,函数就会进行随机选择
def selectJrand(i, m):
j = i # we want to select any J not equal to i
while (j == i):
j = int(random.uniform(0, m))
return j
# 用于调整大于H或小于L的alpha值
def clipAlpha(aj, H, L):
if aj > H:
aj = H
if L > aj:
aj = L
return aj
我给的数据是这样的,文件名叫 testSet_qiu3.txt
0.0 5.0 1
5.0 0.0 1
5.0 5.0 1
1.0 0.0 -1
0.0 1.0 -1
0.0 0.0 -1
这些数据如果画图出来是这样的:
我们用肉眼可以看出超平面应该是这样的:
载入数据:
dataArr, labelArr = loadDataSet('ch06_Data\\testSet_qiu3.txt')
之后是关键,这是简化版SMO算法:
def smoSimple(dataMatIn, classLabels, C, toler, maxIter):
dataMatrix = mat(dataMatIn)
labelMat = mat(classLabels).transpose() # 转置为列向量
# print 'labelMat:', labelMat
b = 0
m, n = shape(dataMatrix) # m行,n列
alphas = mat(zeros((m, 1)))
iter = 0
while (iter < maxIter):
alphaPairsChanged = 0 # pair 一对,成双的
for i in range(m):
fXi = float(multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[i, :].T)) + b
# multiply()相当于点乘
# print 'dataMatrix:', dataMatrix
Ei = fXi - float(labelMat[i]) # if checks if an example violates KKT conditions
if ((labelMat[i] * Ei < -toler) and (alphas[i] < C)) or ((labelMat[i] * Ei > toler) and (alphas[i] > 0)):
# 如果alpha可以更改,进入优化程序
j = selectJrand(i, m)
fXj = float(multiply(alphas, labelMat).T * (dataMatrix * dataMatrix[j, :].T)) + b
Ej = fXj - float(labelMat[j])
alphaIold = alphas[i].copy()
alphaJold = alphas[j].copy()
if (labelMat[i] != labelMat[j]):
L = max(0, alphas[j] - alphas[i])
H = min(C, C + alphas[j] - alphas[i])
else:
L = max(0, alphas[j] + alphas[i] - C)
H = min(C, alphas[j] + alphas[i])
if L == H:
# print "L==H"
continue
eta = 2.0 * dataMatrix[i, :] * dataMatrix[j, :].T - dataMatrix[i, :] * dataMatrix[i, :].T - \
dataMatrix[j, :] * dataMatrix[j, :].T
if eta >= 0:
# print "eta>=0"
continue
alphas[j] -= labelMat[j] * (Ei - Ej) / eta
alphas[j] = clipAlpha(alphas[j], H, L)
# if (abs(alphas[j] - alphaJold) < 0.00001): print "j not moving enough"; continue
alphas[i] += labelMat[j] * labelMat[i] * (alphaJold - alphas[j]) # update i by the same amount as j
# the update is in the oppostie direction
b1 = b - Ei - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] * dataMatrix[i, :].T \
- labelMat[j] * (alphas[j] - alphaJold) * dataMatrix[i, :] * dataMatrix[j, :].T
b2 = b - Ej - labelMat[i] * (alphas[i] - alphaIold) * dataMatrix[i, :] * dataMatrix[j, :].T \
- labelMat[j] * (alphas[j] - alphaJold) * dataMatrix[j, :] * dataMatrix[j, :].T
if (0 < alphas[i]) and (C > alphas[i]):
b = b1
elif (0 < alphas[j]) and (C > alphas[j]):
b = b2
else:
b = (b1 + b2) / 2.0
alphaPairsChanged += 1
# print "iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged)
if (alphaPairsChanged == 0):
iter += 1
else:
iter = 0
# print "iteration number: %d" % iter
return b, alphas
smoSimple函数返回的两个值,一个b,就是wTx+b中的b,而alphas是一个n*1的矩阵,矩阵中的每一个值代表一个数据点对应的alpha。正常情况下这些值大部分都等于0,那些不为0的点就是支持向量。我们这个例子因为数据点比较少,所以非零值比较多。
我们输出看一下b和alphas:
b, alphas = smoSimple(dataArr, labelArr, 0.6, 0.001, 40)
print 'b:', b
print 'alphas:', alphas
输出结果:
b: [[-1.49897588]]
alphas: [[ 0.10818116]
[ 0.14171643]
[ 0. ]
[ 0.20878698]
[ 0.04111061]
[ 0. ]]
找到alphas不是我们的目的,我们的目标是找到wT。我们这样通过alphas求wT:
# 此函数所返回的,就是 WT*X + b 中的WT
def calcWs(alphas, dataArr, classLabels):
X = mat(dataArr)
labelMat = mat(classLabels).transpose()
m, n = shape(X)
w = zeros((n, 1))
for i in range(m):
w += multiply(alphas[i] * labelMat[i], X[i, :].T)
return w
看一看wT张什么样:
>> ws = calcWs(alphas, dataArr, labelArr)
>> print ws
[[ 0.49979518]
[ 0.49979518]]
其实就是:
[[ 0.5]
[ 0.5]]
而b=-1.49897588,其实就是-1.5嘛,所以分类器我们就可以这样写:
我们带入几个已知点试一下,比如,带入(5, 0)应该得+1,带入(5, 5)应该得一个大于+1的数,带入(0, 1)应该得-1:
这样,我们的任务就完成了。(好吧,是最基本的任务。)
我们的822,我们的青春
欢迎所有热爱知识热爱生活的朋友和822实验室一起成长,吃喝玩乐,享受知识。