这一篇真正开始进入深度学习里面的核心操作了－卷积神经网络，这是继Fully-Connected Neural Nets(全连接神经网络)又比较综合的一次作业，难度会有点。作业 ConvolutionalNetworks.ipynb主要是完成卷积中的两种基本操作：convolution和max pooling，之后会放出两种快速版本，然后瞬间觉得自己写的朴素版本被吊着打；之后重点还得完成一下针对卷积里面的归一化：Spatial Batch Normalization（也就是之前说的2D的Batch Normalization）和Group Normalization（2018年提出来的，前一篇博文中也有提到），教程中主要要看的是：

lecture 5（对于视频和lecture的顺序我总感觉很迷）
Convolutional Neural Networks: Architectures, Convolution / Pooling Layers

Convolutional Networks

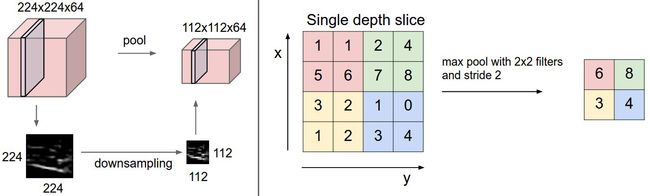
我想对于卷积(convolution)和池化操作(pooling)操作看完上面的教程应该就很清楚了，况且对于学这门课的，多少有点这方面的基础，我就放一张典型的卷积示意图吧(动图来自以上教程)：

来自以上教程的卷积动图

这也来一张池化的示意图，同样来自以上教程中的：

CS231n Spring 2019 Assignment 2—Convolutional Networks卷积神经网络_第2张图片

池化示意图

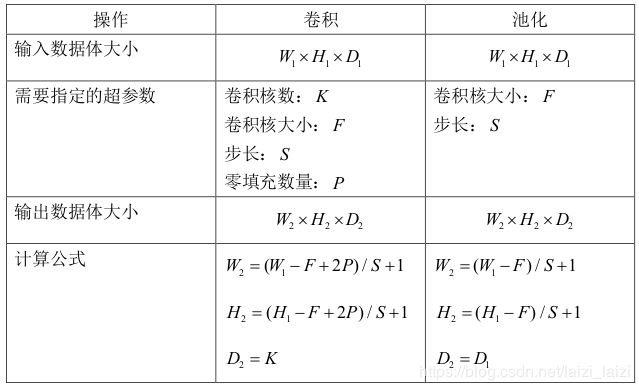
对于最普通的卷积和池化，就如教程里面的提到的(其实卷积里面还有很多别的超参数可以设定的，可以看torch.nn.Conv2d函数的输入参数就可以大致明白了，这里有个动图总结得很好)，我把一些输入输出公式总结了一下：

CS231n Spring 2019 Assignment 2—Convolutional Networks卷积神经网络_第3张图片

卷积和池化的一般公式总结

Convolution: Naive forward pass

在padding操作的时候用了一个numpy.pad()函数，我下面的这句话：

xx = np.pad(x[data_point,:,:,:], pad_width=((0,0),(pad,pad),(pad,pad)), mode='constant')意思就是在x上下左右以常值0围上pad圈

没办法，自己一想只能想到循环的方法，这样写出来还是比较容易懂的，就是卷积核在feature map上依次滑动就完成了2D卷积的操作，其中主要要找到卷积之后的feature map上的点与之前对应的位置关系：
conv_forward_naive(x, w, b, conv_param)--->return out, cache

def conv_forward_naive(x, w, b, conv_param):
    """
    To save space, delete the comment.
    """
    out = None
    ###########################################################################
    # TODO: Implement the convolutional forward pass.                         #
    # Hint: you can use the function np.pad for padding.                      #
    ###########################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    stride = conv_param['stride']
    pad = conv_param['pad']
    N, C, H, W = x.shape
    F, WC, HH, WW = w.shape # actually, WC is equal to C
    H_out = int(1 + (H + 2 * pad - HH) / stride)
    W_out = int(1 + (W + 2 * pad - WW) / stride)
    out = np.zeros((N, F, H_out, W_out))
    # In numpy, 'out[:,:,:]' is equal to 'out' if out has 3-D 
    for data_point in range(N):
        xx = np.pad(x[data_point,:,:,:], pad_width=((0,0),(pad,pad),(pad,pad)), mode='constant')
        for filt in range(F):
            for hh in range(H_out):
                for ww in range(W_out):
                    # Do not forget bias term!!
                    out[data_point, filt, hh, ww] = np.sum(w[filt,:,:,:] * xx[:,stride*hh:stride*hh+HH,stride*ww:stride*ww+WW]) + b[filt]
            
    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    cache = (x, w, b, conv_param)
    return out, cache

Convolution: Naive backward pass

反向传播一向就比前向传播要稍微难写一点。但是最关键的还是要有一个计算图的概念，就是上游梯度该怎么分配给原先feature map中的各个点，分给卷积核中的各个点，以及怎么分配给偏置，其实这时候再去看上面的卷积动图就会很有帮助。

解决思路:在卷积核滑动的过程中，可以想象成有很多的add gate和multiply gate，无非就是上游梯度乘以权值赋给dx，上游梯度乘以feature map中的值赋给dx，而索引还是和前向传播中差不多（索引就是为了划出那块感受野）

dx[n,:,:,:] = dx_x[:,pad:-pad,pad:-pad]这句话就是为了去掉边上那几圈padding，只保留valid那块

conv_backward_naive(dout, cache)--->return dx, dw, db

def conv_backward_naive(dout, cache):
    """
    To save space, delete the comment.
    """
    dx, dw, db = None, None, None
    ###########################################################################
    # TODO: Implement the convolutional backward pass.                        #
    ###########################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    x, w, b, conv_param = cache
    stride = conv_param['stride']
    pad = conv_param['pad']
    N, F, H_out, W_out = dout.shape
    F, WC, HH, WW = w.shape

    dw = np.zeros(w.shape)
    dx = np.zeros(x.shape)
    db = np.zeros(b.shape)

    for n in range(N):
        xx = np.pad(x[n,:,:,:], pad_width=((0,0),(pad,pad),(pad,pad)), mode='constant')
        dx_x = np.zeros(xx.shape)
        for filt in range(F):
            for hh in range(H_out):
                for ww in range(W_out):
                    dw[filt,:,:,:] += dout[n,filt,hh,ww] * xx[:,stride*hh:stride*hh+HH,stride*ww:stride*ww+WW]
                    db[filt] += dout[n,filt,hh,ww]
                    dx_x[:,stride*hh:stride*hh+HH,stride*ww:stride*ww+WW] += dout[n,filt,hh,ww] * w[filt,:,:,:]
        dx[n,:,:,:] = dx_x[:,pad:-pad,pad:-pad]
    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    return dx, dw, db

Max-Pooling: Naive forward

只要之前的卷积的前向传播能写出来了，最大池化的前向传播也是同样的道理，甚至还要更简单，因为想象一下也是一个取最大值的核在feature map上不断地滑动，取出感受野里面的最大值赋给生成的feature map对应点就好了，反正用循环的方法还是很朴素易懂的：
max_pool_forward_naive(x, pool_param)--->return out, cache

def max_pool_forward_naive(x, pool_param):
    """
    To save space, delete the comment.
    """
    out = None
    ###########################################################################
    # TODO: Implement the max-pooling forward pass                            #
    ###########################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    pool_height = pool_param['pool_height']
    pool_width = pool_param['pool_width']
    stride = pool_param['stride']
    N, C, H, W = x.shape

    H_out = int(1 + (H - pool_height) / stride)
    W_out = int(1 + (W - pool_width) / stride)
    out = np.zeros((N, C, H_out, W_out))
    for data_point in range(N):
        for channel in range(C):
            for hh in range(H_out):
                for ww in range(W_out):
                    out[data_point,channel,hh,ww] = np.max(x[data_point,channel,stride*hh:stride*hh+pool_height,stride*ww:stride*ww+pool_width])

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    cache = (x, pool_param)
    return out, cache

Max-Pooling: Naive backward

这时看一下上面的最大池化的图就会帮助理解，核心思路就是：要找到前向传播的时候感受野里面最大值所在的那个索引，只把上游梯度传给它就行了，其他的位置梯度为0。我用了一个np.where()函数，能返回最大值的行列号索引。其实不用这个，直接用mask的思想也可以完成，比如把下面的31-33行改成如下：

mask = temp==np.max(temp)
dx[n,channel,stridehh:stridehh+pool_height,strideww:strideww+pool_width] = dout[n,channel,hh,ww] * mask

max_pool_backward_naive(dout, cache)--->return dx

def max_pool_backward_naive(dout, cache):
    """
    A naive implementation of the backward pass for a max-pooling layer.

    Inputs:
    - dout: Upstream derivatives
    - cache: A tuple of (x, pool_param) as in the forward pass.

    Returns:
    - dx: Gradient with respect to x
    """
    dx = None
    ###########################################################################
    # TODO: Implement the max-pooling backward pass                           #
    ###########################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    x, pool_param = cache
    pool_height = pool_param['pool_height']
    pool_width = pool_param['pool_width']
    stride = pool_param['stride']
    N, C, H, W = x.shape
    _, _, H_out, W_out = dout.shape
    dx = np.zeros(x.shape)

    for n in range(N):
        for channel in range(C):
            for hh in range(H_out):
                for ww in range(W_out):
                    temp = x[n,channel,stride*hh:stride*hh+pool_height,stride*ww:stride*ww+pool_width]
                    index = np.where(temp==np.max(temp))
                    dx[n,channel,stride*hh:stride*hh+pool_height,stride*ww:stride*ww+pool_width][index] = \
                        dout[n,channel,hh,ww]

    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    return dx

fast layers/sandwich

在fast_layers.py里面已经给出了很多快速版本，依赖于Cython扩展，不过这都不用我们弄，接口都跟我们的一样。之后就可以看到快速版本简直分分钟吊打我们的版本，最慢的都比我们快100倍左右（手动捂脸），之后我们就都用这快速版本了（原理还需研究）。

之后就是去layer_utils.py搭建conv_relu_pool_forward, conv_relu_pool_backward, conv_relu_forward, conv_relu_backward几个集成函数，都是简单的调用，想叠三明治一样，这就不多说了。

Three-layer ConvNet

到这里就是用之前的层来搭建一个三层的卷积神经网络并训练一下。架构是conv - relu - 2x2 max pool - affine - relu - affine - softmax，一个卷积加两个仿射，可以考虑用conv_relu_pool_forward、affine_relu_forward和affine_forward函数构建。有了之前的基础层，现在代码会很简洁，具体请看cnn.py

Spatial Batch Normalization

现在的Batch Normalization是对卷积完的feature map做归一化，所以称作Spatial Batch Normalization，也就是2D的，输入shape是(N, C, H, W)，为每一C channel对N,H,W计算统计值。

forward

其实这里不需要真的沿着N,H,W计算均值和方差，只要通过一个reshape再调用之前的batchnorm_forward就行了，这里要注意的一点就是：后面reshape的顺序要和前面的transpose顺序对应：
spatial_batchnorm_forward(x, gamma, beta, bn_param)--->return out, cache

# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

# Note: reshape must be correspond to transpose order
N, C, H, W = x.shape
x = x.transpose(0, 2, 3, 1).reshape(N * H * W, C)
out, cache = batchnorm_forward(x, gamma, beta, bn_param)
out = out.reshape(N, H, W, C).transpose(0, 3, 1, 2)

# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

backward

反向传播也是类似的：
spatial_batchnorm_backward(dout, cache)--->return dx, dgamma, dbeta

# *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

N, C, H, W = dout.shape
dout = dout.transpose(0, 2, 3, 1).reshape(N * H * W, C)
dx, dgamma, dbeta = batchnorm_backward_alt(dout, cache)
dx = dx.reshape(N, H, W, C).transpose(0, 3, 1, 2)

# *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

Group Normalization

这在Batch Normalization那篇中也有提到，Group Normalization和Layer normaliztion很像，是何凯明在2018年的ECCV中提出来的，与Layer normaliztion对每一个data point计算整个feature不同，Group Normalization是把每一个data point的feature分成很多group分别归一化。

forward

因为, 都是(1,C,1,1)的shape，所以我们先用numpy.squeeze()处理了一下，变成shape为(C,)的，然后调用前面的1D的 layernorm_forward，用循环的方式，一组组的归一化：
spatial_groupnorm_forward(x, gamma, beta, G, gn_param)--->return out, cache

def spatial_groupnorm_forward(x, gamma, beta, G, gn_param):
    """
    To save space, delete the comment.
    """
    out, cache = None, None
    eps = gn_param.get('eps',1e-5)
    ###########################################################################
    # TODO: Implement the forward pass for spatial group normalization.       #
    # This will be extremely similar to the layer norm implementation.        #
    # In particular, think about how you could transform the matrix so that   #
    # the bulk of the code is similar to both train-time batch normalization  #
    # and layer normalization!                                                # 
    ###########################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    N, C, H, W = x.shape
    x = x.transpose(0, 2, 3, 1).reshape(N * H * W, C)
    out = np.zeros(x.shape)
    cache = []

    f_p_g = int(C / G) # feature_per_group
    for group in range(G):
        x_piece = x[:,group*f_p_g:group*f_p_g + f_p_g]
        gamma_piece = np.squeeze(gamma)[group*f_p_g:group*f_p_g + f_p_g]
        beta_piece = np.squeeze(beta)[group*f_p_g:group*f_p_g + f_p_g]

        out_piece, cache_piece = layernorm_forward(x_piece, gamma_piece, beta_piece, gn_param)

        out[:,group*f_p_g:group*f_p_g + f_p_g] = out_piece
        cache.append(cache_piece)

    out = out.reshape(N, H, W, C).transpose(0, 3, 1, 2)
    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    return out, cache

backward

反向传播的时候也是一组一组的传给layernorm_backward就行，因为我初始化, 的时候是初始化为1维的，没有初始化为4维的，所以之后就用了numpy.expand_dims()函数，当然可以一开始就初始化成４维的，然后切出来喂给layernorm_backward也行，之后就不用拓展维度了：
spatial_groupnorm_backward(dout, cache)--->dx, dgamma, dbeta

def spatial_groupnorm_backward(dout, cache):
    """
    To save space, delete the comment.
    """
    dx, dgamma, dbeta = None, None, None

    ###########################################################################
    # TODO: Implement the backward pass for spatial group normalization.      #
    # This will be extremely similar to the layer norm implementation.        #
    ###########################################################################
    # *****START OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****

    N, C, H, W = dout.shape
    G = len(cache)
    f_p_g = int(C / G) # feature_per_group
    dout = dout.transpose(0, 2, 3, 1).reshape(N * H * W, C)

    dx = np.zeros(dout.shape)
    dgamma = np.zeros(C)
    dbeta = np.zeros(C)


    for g in range(G):
        dout_piece = dout[:,g*f_p_g:g*f_p_g+f_p_g]
        
        dx_p, dgamma_p, dbeta_p = layernorm_backward(dout_piece, cache[g])

        dx[:,g*f_p_g:g*f_p_g+f_p_g] = dx_p
        dgamma[g*f_p_g:g*f_p_g+f_p_g] = dgamma_p
        dbeta[g*f_p_g:g*f_p_g+f_p_g] = dbeta_p

    dx = dx.reshape(N, H, W, C).transpose(0, 3, 1, 2)
    dgamma = np.expand_dims(dgamma, axis=0)
    dgamma = np.expand_dims(np.expand_dims(dgamma, axis=-1), axis=-1)
    dbeta = np.expand_dims(dbeta, axis=0)
    dbeta = np.expand_dims(np.expand_dims(dbeta, axis=-1), axis=-1)
    
    # *****END OF YOUR CODE (DO NOT DELETE/MODIFY THIS LINE)*****
    ###########################################################################
    #                             END OF YOUR CODE                            #
    ###########################################################################
    return dx, dgamma, dbeta

结果

具体结果请看：ConvolutionalNetworks.ipynb

链接

前后面的作业博文请见：

CS231n Spring 2019 Assignment 2—Convolutional Networks卷积神经网络

Convolutional Networks

Convolution: Naive forward pass

Convolution: Naive backward pass

Max-Pooling: Naive forward

Max-Pooling: Naive backward

fast layers/sandwich

Three-layer ConvNet

Spatial Batch Normalization

forward

backward

Group Normalization

forward

backward

结果

链接

你可能感兴趣的:(CS231n Spring 2019 Assignment 2—Convolutional Networks卷积神经网络)