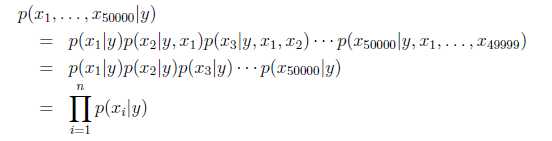1:演变关系
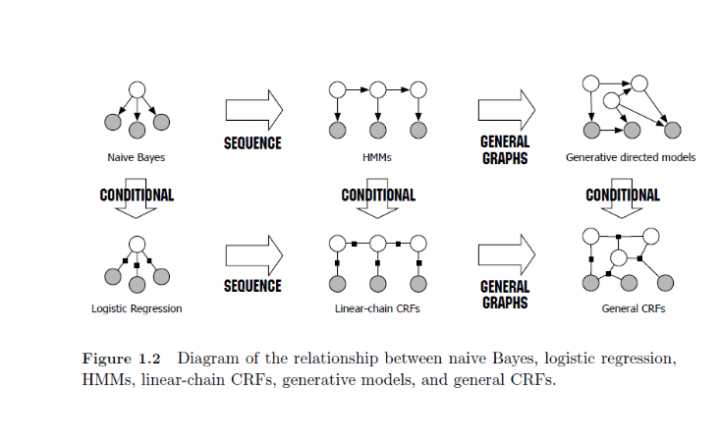
上边的图是
这一篇论文中的一个截图,而第一张图其实讲的是几种模型的演进的一个过程,而这个过程如果加以简单的概括的话,可以归类于上边的一栏为产生型模型,下边的一栏为判别型模型,那这两种模型有什么区别,这两种模型又是什么?接下来我们分别来掰扯掰扯这两种模型.
1:产生型模型
定义: 由数据学习联合概率密度分布P(X,Y),然后求出条件概率分布P(Y|X)作为预测的模型,即生成模型:P(Y|X)= P(X,Y)/ P(X).
那产生型模型的典型代表其实就是朴素贝叶斯.这一种的模型的主要思想是先估算联合概率密度p(x,y),再通过贝叶斯公式求出p(y|x).那现在我们就以之前文章中所说过的垃圾邮件分类的例子再来讲一下产生型模型的处理方法.
现在我们假设要分类垃圾邮件和正常的邮件(分类处理邮件是文本分类和模式识别的一种典型应用),现在我们假设采用最简单的特征描述的方法,首先我们先去找一个词库,然后把词库中的单词都归类起来,然后把每一封邮件表示成一个向量,向量中的每一维都是词库中一个词的0-1值,1表示出现这个词语,0表示没有出现这个词语.
比如一封邮件出现了”伟哥”,”理财”,”投资”,却没有出现”邀请”,”还款”,”金融”这样的词语,我们就可以把这个向量表示为:(mathtype没法输入中文,所以用拼音代替了)
如果这个词库里的词语过多,我们的x的维度也会很大,这时候我们就应该要采取一些比如多项式分布模型的方法来去简化计算,这个我们就不多做讨论.
回到上边的垃圾邮件问题中来,对于邮件,我们大致上可以将每一封邮件看作是相互独立的,这样每一次我们取一封邮件就可以看作是一次随机事件,那么我们的可能性就会有2的n次方种可能性,这样我们处理起来参数过多,那也就没有什么实用价值.
那这时候我们如果用生成模型去做,就会有新的思路,我们要求的是p(y|x),那么按照条件概率公式可以的到,我们只需要求p(x|y),p(z),那么如果假设邮件x之间是相互独立的,这个就可以说符合贝叶斯假设,举个例子说:
假设我们去判别一封邮件已经是垃圾邮件了(y=1),并且这个邮件出现”伟哥”和出现其他的词是无关的,那么就说”伟哥”和其他的词是相互独立的.
那现在我们假设:
给定条件z,使得X,Y条件独立,那形式化可以表示为:
那如果词库中出现了5000个词语,我们全部把词语放进来,这时候我们再回到问题中,就可以根据上式列出公式来:
而这一步的处理其实和我们之前的文章的n元语法模型是类似的,但是这里边说的是每个词语之间是相互独立的,而”伟哥”和”性”,一般来说是有很大的关系的,这样的词汇会经常出现在垃圾邮件中.
那现在我们建立形式化的模型: