22. Representations of graphs

There are 2 ways to display a graph:

1. adjacency list
2. adjacency matrix

The space and time complexity of the matrix are n^2, which is quite large and inefficient for the practice.

Graph searching techniques:

1. Breadth First Search (BFS)
2. Depth First Search (DFS)

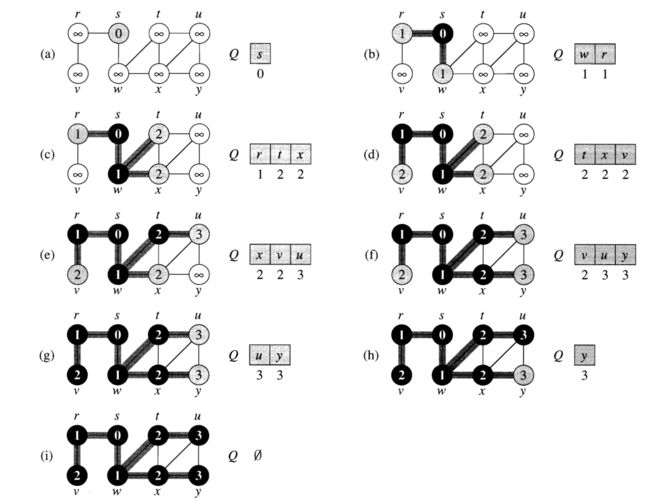
1. Breadth First Search

To keep track of BFS search progress, we color each vertex in a graph with one of following three colors.
a. WHITE – not visited yet
b. GRAY – visited but don’t check all its neighbors yet
c. BLACK – visited and finished looking at all its neighbors

To implement this search, we need a data structure:

1. Queue: dequeue and enqueue.
2. 3 attributes of the vertices:
   color : WHITE, GRAY or BLACK
   distance : an integer (the distance of v from the starting vertex)
   pointer: the parent pointer that points to another vertex

Property of BFS

1. All the vertices reachable from s are visited in order of their distance from s.
2. The final value of v. d is infinite if v is not reachable from s, and the distance
3. The edges (v. pointer, v) for all v belongs to V together form a tree.
   from s to v otherwise.

Time complexity: Each vertex is initialized once and put into the queue once.
Each edge is examined twice from each of its two endpoints.
Therefore, the total time for BFS traversal on a graph G(V,E) is O(|V|+|E|), where |V| is the number of vertices and |E| is the number of edges.

Application

1. Distances in a graph.(Note that this is only for graphs where all edges have the same length.)
2. Connected components of an undirected graph.
3. Coloring a bipartite graph.
   An undirected graph G(V,E) is a bipartite graph if its vertex set can be colored with two colors such that every edge has one endpoint of each color.

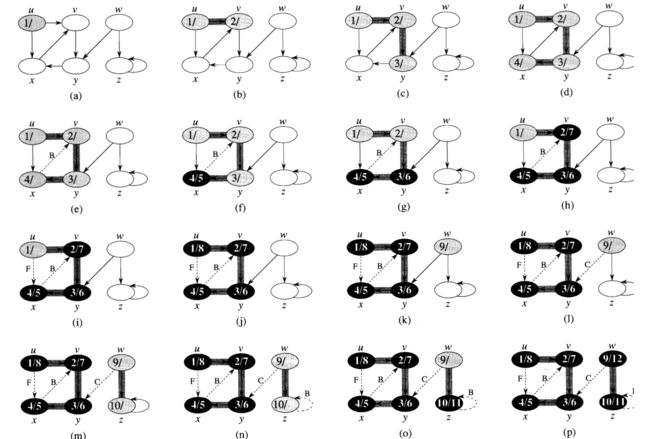
Depth First Search -- backtracking search

Moves “forward” when possible, and only “backtracks” when moving forward is impossible.
Data structure:
The Stack should be used instead of Queue. (This stack can either by represented explicitly (by a stack data-type in our language) or implicitly when using recursive functions.)

As well as the BFS, there are more attributes：

1. time : a global clock with values 0,1,2,...
2. v.d : discovery time (when v is first visited)
3. v. f : finishing time (when all the neighbours of v have been examined)

59E9C0B6-896F-4E6C-BC10-5AB71B65A54A.png

.

Running Time
First of all, the vertices need to be initialized( |v| ), then DFS will work on all the neighbours (|E|).

Edge classification in DFS

DFS classifies the edges in a directed graph into four types.

1. Tree edges (edges along which a vertex is first discovered)
2. Back edges (edges from a descendant to an ancestor)
3. Forward edges (non-tree edges from an ancestor to a descendant)
4. Cross edges (all other edges)

In an undirected graph, edges (u, v) and (v, u) are the same, so we cannot distinguish between forward edges and back edges.
For such a graph, a non-tree edge between a pair of vertices that one is an ancestor of the other is referred to as a back edge.
Theorem: In a depth-first search of an undirected graph G, each edge of G is either a tree edge or a back edge.

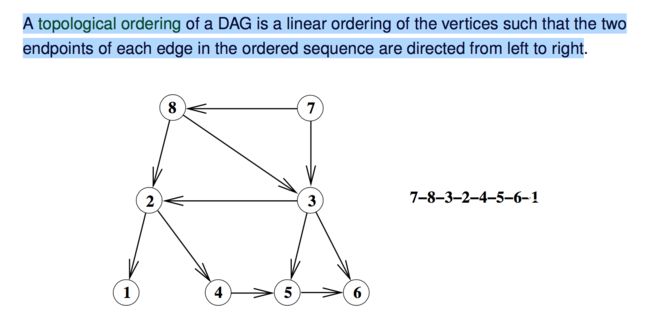
Topological Sorting

A directed graph G(V,E) is called acyclic if it does not contain a directed cycle. Such a graph is also referred to as a Directed Acyclic Graph (DAG).

Theorem
A directed graph G has a directed cycle if and only if a depth-first search of G yields a back edge.
Theorem
Perform DFS on a directed acyclic graph G. Then, the vertex sequence listed by the decreasing order of their finishing time forms a topological ordering for G.