0 准备工作
首先,确认环境中有numpy、scipy.stats和tkinter三个功能包。前两个功能包可用于Python的数学计算,比如使用numpy来生成随机数用于Monte Carlo模拟,以及使用scipy.stats包来计算正态分布概率累积函数,这两个功能包可以使用pip安装。而第三个功能包tkinter是Python自带的一个GUI系统,理论上已经整合在了你的Python环境中。所谓的GUI(Graphical User Interface),可以理解为是一个照顾使用者感情,善于跟使用者打交道的系统。我们必须假定使用我们程序的人,比如你在商学院的某个同学,喜欢一看就能明白的界面。他或许并不需要学会使用Console,就能比你赚更多的钱。
需要注意的一点是,虽然scipy已经集成了scipy.stats,但是引用需要单独操作。
其次,要对期权的基本定价方法有一定的了解。一个欧式看涨期权,其到期日的支付为max(S - K, 0),看跌期权为max(K - S, 0). 其中,S为到期日标的资产的价格,K为行权价格。对于一个非常简单的欧式期权,只要掌握几个基本参数,就可以对其进行定价。比如使用著名的Black-Scholes模型,或使用二叉树模型(后被证明其极限情况就是BS公式),或使用Monte Carlo方法(似乎是无懈可击但比较烧钱的方法)。这篇笔记将使用BS公式和Monte Carlo方法来对简单的期权进行定价,所以要对这两个方法使用的公式有所了解。
Black-Scholes的看涨期权和看跌期权的定价法分别如下:
其中F为标的资产的远期价格,下式中的q为连续红利率:
两个小d的公式则是:
Monte Carlo方法则更为简单粗暴,易于理解。在拙作 《使用Python描绘Markowitz有效边界》中曾提到过Monte Carlo方法。在使用Monte Carlo计算期权价格时,假设标的资产每天的收益率是个均值为0,标准差为给定值的random walk. 则我们可以模拟给定时间以后标的资产可能的价格,针对每一个价格给出期权的获利水平,将其折现并取平均值。模拟股价的公式如下:
其中,z是一个服从标准正态分布N(0, 1)的随机变量。
到现在为止,我们已经对欧式期权定价的理论基础有所了解。打开你的Python代码编辑器,你便完成了所有的准备工作。
1 编写一个期权类
“万物皆对象”,既然我们需要针对一个欧式期权进行计算,不妨将期权编写成一个类,在将某个期权实例化为对象时,将其各种属性赋予这个对象。
编写类时,要先给类起一个名字,比如Option.
# -*- coding: utf-8 -*-
from tkinter import *
import numpy as np
import scipy.stats as sps
class Option:
然后想象一下,一个欧式期权应该具有哪些属性,从而编写一个初始化函数。我们的欧式期权,应该具有以下几个属性。
- 看涨或看跌(c or p)
- 标的资产现价(S0)
- 期权执行价格(K)
- 期权到期时间(t)
- 适用的无风险利率(rf)
- 适用的波动率(sigma)
- 股利信息(本例中使用连续股利率dv)
也就是说,为了构造一个欧式期权对象(或为了计算期权的价格),我们至少要知道上面的七个信息。换言之,程序的使用者要输入这七个信息,才能构造一个期权对象。因此,我们的初始化函数要从输入端读取七个变量。
class Option:
def __init__(self, cp, s0, k, t, r, sigma, dv=0):
self.cp = 'Call' if (cp == 'C' or cp == 'c') else 'Put'
self.cp_sign = 1.0 if self.cp == 'Call' else -1.0
self.s0 = s0 * 1.0
self.k = k * 1.0
self.t = t * 1.0
self.sigma = sigma * 1.0
self.r = r * 1.0
self.dv = dv * 1.0
初始化函数的名字是有规定的,叫做"__init__",应该是英语initialize的简写。它的参数有8个,第一个叫做self,它代表了对象本身。在编写一个类时,所有的方法(函数)都要有self这个参数,并默认放在第一个位置。在初始化函数中,我们用self.xxx的方式为类的实例规定它们的属性。如定义self.dv = dv * 1.0,即赋予了实例一个名为dv的属性,并赋值为从输入端读取的dv.
参数的读取区中,dv=0表示dv不是一个强制参数,如果我们不输入dv,则它的值为默认的0.
输入期权的看涨和看跌属性时,我们可以自定义一些规则,我在这里使用的规则是,如果输入的是'c'或'C'则视为看涨期权,否则则视为看跌期权。为了将期权的看涨或看跌属性(字符串类型)转化为可用于计算的数字类型,我们创造一个cp_sign属性,用来储存期权在定价时应使用的符号。
这里要讲一个语法是Python的三元表达式,self.cp = 'Call' if (cp == 'C' or cp == 'c') else 'Put'这个语句的意思是说,如果cp读取的值是'c'或'C',则self.cp值为'Call',否则为'Put'.
我们赋予了一个实例七个基本信息,其实我们还可以将衍生出来的固定不变的信息作为属性写入初始化函数。比如对于给定的欧式期权(对于给定的七个信息),d1和d2变量是不变的。因此,将它们也写入初始化函数,作为期权的一个基本属性。事实上,N(d2)是有意义的,它是风险中性条件下,到期日标的资产价格大于执行价格的概率。因此,我们将初始化函数强化如下。
class Option:
def __init__(self, cp, s0, k, t, r, sigma, dv=0):
self.cp = 'Call' if (cp == 'C' or cp == 'c') else 'Put'
self.cp_sign = 1.0 if self.cp == 'Call' else -1.0
self.s0 = s0 * 1.0
self.k = k * 1.0
self.t = t * 1.0
self.sigma = sigma * 1.0
self.r = r * 1.0
self.dv = dv * 1.0
self.d_1 = (np.log(self.s0 / self.k) + (self.r - self.dv + .5 * self.sigma ** 2) * self.t) / self.sigma / np.sqrt(self.t)
self.d_2 = self.d_1 - self.sigma * np.sqrt(self.t)
到此为止,我们已经初步建立了一个期权类了。我们不妨试验一下对这个类进行实例化。
o = Option('c', 50, 50, 1, .02, .05)
print(o.k)
print(o.t)
print(o.d_2)
其结果如下:
1.0
50.0
0.375
我们发现,调用初始化函数的方法,就是使用类名作为函数名;一旦我们实例化成功,即可轻松调用对象的属性。
2 为期权类添加Black-Scholes公式定价方法
接下来,我们要完善我们的类,为类添加初始化函数之外的其他函数和方法。既然要做一个期权计算器,我们就要加上BS公式和MC模拟两个函数(方法),使其返回数值分别为两个方法的定价结果。
首先来添加BS公式定价法。在类中,除了几个特定功能的函数或方法(如初始化函数)有一定的命名规则,其他的函数我们都可以自定义其名称。比如,我想给BS公式定价函数命名为bsprice(). 跟其它函数一样,它的参数中至少有一个self,事实上我们也只用到了self.
def bsprice(self):
return self.cp_sign * self.s0 * np.exp(-self.dv * self.t) * sps.norm.cdf(self.cp_sign * self.d_1) \
- self.cp_sign * self.k * np.exp(-self.r * self.t) * sps.norm.cdf(self.cp_sign * self.d_2)
这个方法,直接把BS公式的定价值返回。标准正态分布概率累积函数可以使用scipy.stats包中的norm.cdf函数实现。这里,self的cp_sign属性就可以作为符号参与到计算中去了。
其实,我们也可以把这个公式写在初始化函数中,使这个定价值成为期权类的一个属性。在此例中,MC方法是不能定义为属性的,因为MC方法每执行一次,结果都会不一样,而我们并不想多次初始化同一个期权对象。为了和MC方法保持一致,在这里为BS公式单独编写一个方法。
需要注意的是,最新的PEP 8规定,最大行长度为79字符,因此,可以在公式中间换行,这时要使用斜杠\\作为换行标识。
试着调用bsprice方法,注意这是类内的方法,需要使用类名或实例(对象)名调用该方法。
print(o.bsprice())
结果为
1.5603457303145518
3 为期权类添加Monte Carlo定价方法
Monte Carlo方法的精髓在于,根据一定逻辑模拟出大量变量可能的终值。在之前的理论中,我们已经知道,需要生成的只是大量服从标准正态分布N(0, 1)的随机变量。这个可以使用numpy包中的random.normal函数实现,该函数读取三个变量,即均值,标准差(而非方差)和产生个数(默认为1),输出结果为numpy包独有的ndarray数组。
根据公式,我们可以这样编写这个方法。
def mcprice(self, iteration=1000000):
zt = np.random.normal(0, 1, iteration)
st = self.s0 * np.exp((self.r - self.dv - .5 * self.sigma ** 2) * self.t + self.sigma * self.t ** .5 * zt)
p = []
for St in st:
p.append(max(self.cp_sign * (St - self.k), 0))
return np.average(p) * np.exp(-self.r * self.t)
在以上代码中,mcprice的参数多了一个iteration参数,默认为1000000. 该参数为模拟次数,即生成随机数的长度(normal函数的第三个参数)。使用数组可以对模拟的股价进行批量操作。该方法最后返回的是支付平均值的折现值。
试着调用mcprice方法,注意这是类内的方法,需要使用类名或实例(对象)名调用该方法。
print(o.mcprice())
结果为
1.5934012203189629
可以发现跟BS公式的结果十分接近。如果我们将模拟次数减小到10次,并运行10次。
for _ in range(10):
print(o.mcprice(10))
得到的结果为
1.23243207993
2.22651406977
2.00053344972
1.63522616653
1.31759603822
1.85962392016
1.28087686074
1.18089948626
3.04292929062
1.79343397391
因此我们可以知道,MC模拟的次数很小时,其结果是非常不准确的。
到此为止,我们写出了一个完整的欧式期权类。
from tkinter import *
import numpy as np
import scipy.stats as sps
class Option:
def __init__(self, cp, s0, k, t, r, sigma, dv=0):
self.cp = 'Call' if (cp == 'C' or cp == 'c') else 'Put'
self.cp_sign = 1.0 if self.cp == 'Call' else -1.0
self.s0 = s0 * 1.0
self.k = k * 1.0
self.t = t * 1.0
self.sigma = sigma * 1.0
self.r = r * 1.0
self.dv = dv * 1.0
self.d_1 = (np.log(self.s0 / self.k) + (self.r - self.dv + .5 * self.sigma ** 2) * self.t) / self.sigma / np.sqrt(self.t)
self.d_2 = self.d_1 - self.sigma * np.sqrt(self.t)
def bsprice(self):
return self.cp_sign * self.s0 * np.exp(-self.dv * self.t) * sps.norm.cdf(self.cp_sign * self.d_1) \
- self.cp_sign * self.k * np.exp(-self.r * self.t) * sps.norm.cdf(self.cp_sign * self.d_2)
def mcprice(self, iteration=1000000):
zt = np.random.normal(0, 1, iteration)
st = self.s0 * np.exp((self.r - self.dv - .5 * self.sigma ** 2) * self.t + self.sigma * self.t ** .5 * zt)
p = []
for St in st:
p.append(max(self.cp_sign * (St - self.k), 0))
return np.average(p) * np.exp(-self.r * self.t)
4 使用tkinter画一个计算器
tkinter是Python自带的一个GUI系统,它的优点在于不用安装任何的插件,缺点则在于没有可视化过程,非常麻烦,而且很丑,因此很多同学都转向了wxpython或PyQt等工具。其实,使用MS EXCEL VBA也可以编写类似的功能,而且非常容易。在这里使用tkinter,只是为了将这个轻量级的工具用法记录在这里。另外,tkinter的简单入门,可以参考大神辛星的笔记,介绍的十分浅显易懂,非常推荐。
首先,给我们的小窗口起一个名字,叫做root,把它实例化(没错,小窗口也是一个对象)。
from tkinter import *
root = Tk() # Create an object
root.wm_title('European Option Price Calculator')
Label(root, text='Please input relevant parameters, '
'then click "Calculate" button.').grid(row=0, column=0, columnspan=3)
Label(root, text='by Johnny MOON, COB @UIUC').grid(columnspan=3)
以上的几行代码意思是给小窗口起一个标题,并且写上两句前言。Label插件的意思就是现实一段文字,其第一个参数是小窗口的名字root,表示这个Label是要放在root上的。使用grid()方法将Label画在root中。如果不规定row参数,则新的Label将紧跟上一个Label. columnspan参数规定了Label的宽度,在这里定为3,是因为我们之后的grid网格布局中,将大致有三列。
试着使用小窗口的mainloop方法运行一下这个小程序。
root.mainloop()
可以看到弹出了一个窗口。
非常丑。
接下来,就要添加输入各项参数的地方了。首先是期权的看涨或看跌属性。因为只有看涨和看跌,我们可以使用一个单选框,并把用户选择的结果存在另一个类StringVar的实例cp里,实现方法如下。
cp = StringVar()
Label(root, text='Option Type').grid(row=2, column=0, sticky=W)
Radiobutton(root, text='Call', variable=cp, value='c').grid(row=2, column=1)
Radiobutton(root, text='Put', variable=cp, value='p').grid(row=2, column=2)
Radiobutton就是单选框了,可以看到variable参数指定为了cp,即之前定义的一个StringVar类对象,它的意思是说,选中这个单选框,将改变cp的值。那么改变为多少呢,由value参数来确定。我们在未来还要用到cp的值,彼时使用cp.get()即可调用。
同样使用grid方法将其放在我们想要的地方。sticky参数决定了插件要不要贴边摆放,其参数可以是E, S, W, N以及它们通过'+'号的组合。注意它们并不是字符型。再次执行mainloop()方法可以发现窗口发生了变化。
接下来绘制参数输入部分,可以偷个懒使用一个for循环。
plist = ['Current Price', 'Strike Price', 'Days to Maturity',
'Risk-free Rate', 'Volatility', 'Continuous Dividend Rate', 'MC Iteration']
elist = []
r = 3 # r start from 0 and now is 3
for param in plist:
Label(root, text=param).grid(column=0, sticky=W)
e = Entry(root)
e.grid(row=r, column=1, columnspan=2, sticky=W+E)
elist.append(e)
r += 1
Entry就是输入框了,而且一般不用输入其他参数。Entry因为要记录一些参数,所以不能用而弃之,因此先储存在一个列表elist中,之后计算时要进行调用。储存完毕后,再将其使用grid方法画到root里。使用r记录行数便于现在和之后的布局。
执行mainloop方法看一看效果。
这些输入框中,就是我们进行期权对象初始化,以及期权定价方法所需的所有参数了。
最后一步是绘制计算按钮和答案显示区。
Button(root, text='Calculate').grid(row=r)
r += 1
answ = Label(root, text='The result is as follows:')
answ.grid(row=r, columnspan=3)
r += 1
bs = Label(root)
mc = Label(root)
bs.grid(row=r, columnspan=2, sticky=E)
mc.grid(row=r+1, columnspan=2, sticky=E)
Label(root, text='Use BS formula: ').grid(row=r, sticky=W)
Label(root, text='Use Monte Carlo: ').grid(row=r+1, sticky=W)
这部分代码有四部分,第一部分是绘制一个按钮,Button就是用来初始化按钮的函数了,按钮上的文字是"Calculate",按钮的功能我们将在下一部分定义;第二部分是绘制一行答案提示文字;第三部分是答案显示区,目前还没有答案可以显示;第四部分是用来提示答案是用什么方法得到的。
每一部分定义好了之后,都使用grid方法放到root中,执行mainloop()查看一下。
可以看到,一个计算器的框架已经画好了,单选框的确只能选一个,而输入框则可以输入任何文字。说明这个GUI已经在向使用者索要参数值输入了。
至于Calculate按钮,目前只是一个嘴炮,点下去并没有任何作用。
5 将GUI收集的参数加入计算
这个部分将介绍如何给予刚刚绘制出的计算器以灵魂。我们想要的功能是,在输入了各项参数之后,点击Calculate按钮,右下角就出现两个不同方法得出的期权定价结果。
那么关键就在于,按了Calculate之后,Python到底做了什么。Button初始化时有一个参数叫做command,我们之前并没有用到,它规定了按了Button以后会执行什么方法。
因此,我们需要先编一个方法,规定一下按了Button以后干嘛。这个方法的功能主要有
- 检查输入参数是否正确
- 根据输入参数进行期权价值计算
首先是检查参数是否正确,我们先观察一下对参数的要求。
- 所有输入框应输入实数;
- 除无风险利率外,所有输入框应输入非负数;
- MC模拟次数应设定为整数
首先写一个空列表vlist来收集各个输入框的数值,之前有一个列表elist抓取了所有的输入框,现在我们就可以对它处理。建立好vlist后,开始进行参数收集,如果有参数不是实数,进行报错。
def calc():
vlist = []
for e in elist:
try:
p = float(e.get())
vlist.append(p)
except:
answ.config(text='Invalid Input(s). Please input correct parameter(s)', fg='red')
e.delete(0, len(e.get()))
return 0
在拙作《使用Python的Text Processing方法爬取IMDb TOP 250榜单电影列表》中,介绍过try/except语句的用法,上面这段代码就是使用try/except语句测试一下我们输入的字符串能不能变为浮点类型,如果不能,就删除该字符串,并提示输入正确的字符串。实现删除输入框内容的方法是delete,它的第一个参数代表位置(0代表最开头),第二个参数代表长度,此处删除整个字符串长度。我们将之前定义Calculate按钮的语句稍作修改. 实现提示的方法是config,他可以改变插件的一些属性,上述代码将原本的答案提示信息修改成了报错信息,并使用了红色字体。
Button(root, text='Calculate', command=calc).grid(row=r)
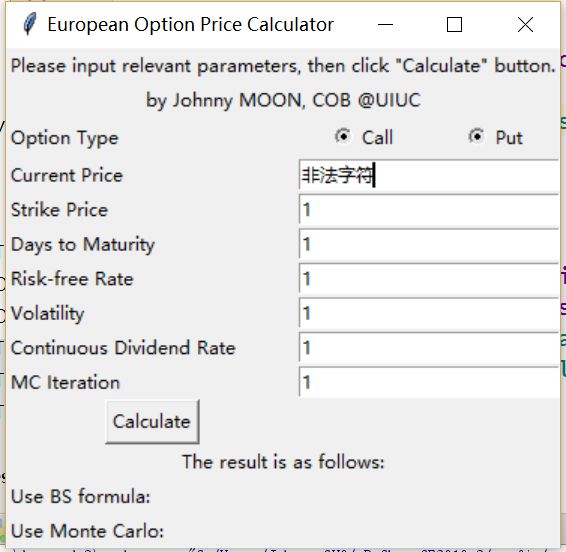
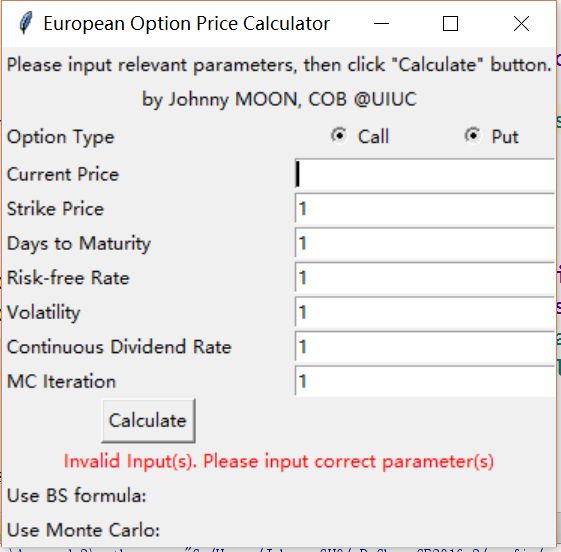
现在,Calculate按钮已经可以执行不完整的calc方法了,效果如下。
只要出现非法输入,calc程序return 0而结束,再次输入再次点击,calc程序将重新运行。使用相同的方法,将非负数条件加入calc中。
for i in range(6):
if i != 3 and vlist[i] < 0:
answ.config(text='Invalid Input(s). Please input correct parameter(s)', fg='red')
elist[i].delete(0, len(elist[i].get()))
return 0
前两道关卡保证了所有数字的合法性。最后一个MC模拟次数的输入框,我们默认将小于1000或大于10000000的次数分别自动设定为1000和10000000,实现方法如下。
vlist[6] = int(vlist[6])
if vlist[6] < 1000:
vlist[6] = 1000
elist[6].delete(0, len(elist[6].get()))
elist[6].insert(0, '1000')
elif vlist[6] > 10000000:
vlist[6] = 10000000
elist[6].delete(0, len(elist[6].get()))
elist[6].insert(0, '10000000')
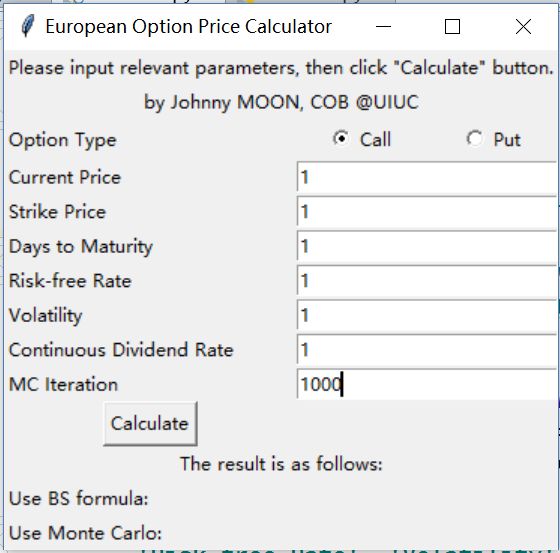
在这里使用insert函数,用法与delete函数一致。注意上面代码中,不但修改了输入框显示的数字,也修改了vlist收集的值,否则后来计算时,还将使用之前不符合规则的值。这个规则效果如下。
如果calc程序能进行到这里,说明所有的基本信息都已经收集完毕,而且合法。此时,我们用config将报错信息改为原来的答案提示信息,并改回黑色字体。现在,使用收集的期权基本信息定义期权类的一个实例o,要注意t的单位是年,初始化时要先年化。调用o的bsprice和mcprice方法,将答案区修改为返回的两个值,并保留8位小数。
o = Option(cp.get(), vlist[0], vlist[1], vlist[2] / 365, vlist[3], vlist[4], vlist[5])
answ.config(text='The result is as follows:', fg='black')
bs.config(text=str("%.8f"%o.bsprice()))
mc.config(text=str("%.8f"%o.mcprice(iteration=vlist[6])))
观看一下效果。
本篇笔记是两次FIN 514作业的集合体,涉及到的逻辑比较初级。期权的定价是Monte Carlo方法的一个十分简单的应用。随着科技的发展,MC方法的成本也将逐渐降低。
本篇笔记一并记录了面向对象编程的简单入门。面向对象编程对于商学院的学生来说并没有那么可怕,从任何想象中的对象开始就好了。
本篇笔记也记录了tkinter的简单应用。要注意此处使用的是Python 3,如果使用Python 2的话,tkinter的import方法有所不同。在此再次推介辛星大神的tkinter教程。今后也将研究一下wxpython和PyQt,以更方便地制作GUI.
如果您发现任何问题或有任何疑问,欢迎指正或讨论。
by JohnnyMOON, COB @UIUC
这是做Finance作业的学习笔记
EM: [email protected]