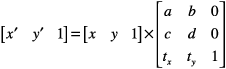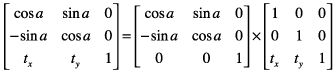版本记录
| 版本号 | 时间 |
|---|---|
| V1.0 | 2018.09.05 |
前言
Quartz 2D框架相信大家都知道,也都一直在使用。Quartz 2D的API是纯C语言的,它是一个二维绘图引擎,同时支持iOS和Mac系统。Quartz 2D的API来自于Core Graphics框架,数据类型和函数基本都以CG作为前缀,接下来几篇我们就一起来看一下这个框架。感兴趣可以看上面几篇文章。
1. Quartz 2D编程指南 (一) —— 简介(一)
2. Quartz 2D编程指南 (二) —— Quartz 2D概览(二)
3. Quartz 2D编程指南 (三) —— 图形上下文(三)
4. Quartz 2D编程指南 (四) —— Paths路径(一)
5. Quartz 2D编程指南 (五) —— Paths路径(二)
6. Quartz 2D编程指南 (六) —— 颜色和颜色空间(一)
Transforms - 变换
Quartz 2D绘图模型定义了两个完全独立的坐标空间:用户空间(表示文档页面)和设备空间(表示设备的原始分辨率)。用户空间坐标是与设备空间中像素分辨率无关的浮点数。当您想要打印或显示文档时,Quartz会将用户空间坐标映射到设备空间坐标。因此,您无需重写应用程序或编写其他代码来调整应用程序的输出,以便在不同设备上实现最佳显示。
您可以通过在当前转换矩阵(current transformation matrix)或CTM上操作来修改默认用户空间。创建图形上下文后,CTM是单位矩阵。您可以使用Quartz转换函数来修改CTM,从而修改用户空间中的绘图。
本章:
- 概述了可用于执行转换的函数
- 显示如何修改CTM
- 描述如何创建仿射变换
- 显示如何确定两个转换是否相同
- 描述如何获取用户到设备空间的转换
- 讨论仿射变换背后的数学
About Quartz Transformation Functions - 关于Quartz转换函数
您可以使用Quartz 2D内置转换函数轻松转换,缩放和旋转绘图。 只需几行代码,您就可以按任何顺序和任意组合应用这些转换。 图5-1说明了缩放和旋转图像的效果。 您应用的每个转换都会更新CTM。 CTM始终表示用户空间和设备空间之间的当前映射。 此映射可确保应用程序的输出在任何显示屏或打印机上都很好看。
Quartz 2D API提供了五个函数,允许您获取和修改CTM。 您可以旋转,平移和缩放CTM,并且可以将仿射变换矩阵与CTM连接起来。 请参阅Modifying the Current Transformation Matrix。
在您决定将变换应用于CTM之前,Quartz还允许您创建不在用户空间上运行的仿射变换。 您使用另一组函数来创建仿射变换,然后可以将其与CTM连接。 请参阅Creating Affine Transforms。
您可以使用任一组函数,而无需了解有关矩阵数学的任何信息。 但是,如果您想了解Quartz在调用其中一个变换函数时所执行的操作,请阅读The Math Behind the Matrices。
Modifying the Current Transformation Matrix - 修改当前转换矩阵
在绘制图像之前,您可以操纵CTM以旋转,缩放或平移页面,从而转换要绘制的对象。 在转换CTM之前,需要保存图形状态,以便在绘制后恢复它。 您还可以将CTM与仿射变换连接起来(请参阅Creating Affine Transforms)。 本节将介绍这四个操作中的每一个 - 转换,旋转,缩放和连接,以及执行每个操作的CTM函数。
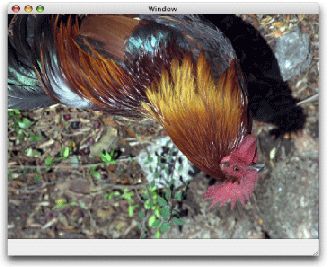
下面的代码行绘制一个图像,假设您提供了一个有效的图形上下文,一个指向矩形的指针以绘制图像,以及一个有效的CGImage对象。 代码绘制图像,例如图5-2中所示的样本公鸡图像。 在阅读本节的其余部分时,您将看到在应用转换时图像如何变化。
CGContextDrawImage (myContext, rect, myImage);
平移将坐标空间的原点移动为您为x和y轴指定的量。 您调用函数CGContextTranslateCTM以按指定的量修改每个点的x和y坐标。 图5-3显示了使用以下代码行转换为x轴100个单位和y轴50个单位的图像:
CGContextTranslateCTM (myContext, 100, 50);
旋转将坐标空间移动指定的角度。 您可以调用函数CGContextRotateCTM来指定旋转角度,以弧度为单位。 图5-4显示了一个图像围绕原点旋转了-45度,这是窗口的左下角,使用以下行。
GContextRotateCTM (myContext, radians(–45.));
图像被剪裁,因为旋转将图像的一部分移动到上下文之外的位置。 您需要以弧度为单位指定旋转角度。
如果您计划执行多次旋转,则编写弧度例程很有用。
#include
static inline double radians (double degrees) {return degrees * M_PI/180;}
缩放通过您指定的x和y因子更改坐标空间的比例,从而有效地拉伸或缩小图像。 x和y因子的大小决定新坐标是大于还是小于原始坐标。 另外,通过使x因子为负,可以沿x轴翻转坐标; 类似地,您可以通过使y因子为负,沿y轴水平翻转坐标。 您可以调用函数CGContextScaleCTM来指定x和y缩放因子。 图5-5显示了一个图像,其x值按.5缩放,其y值按.75缩放,使用以下代码行:
CGContextScaleCTM (myContext, .5, .75);
连接通过将两个矩阵相乘来组合两个矩阵。 您可以连接多个矩阵以形成包含矩阵累积效应的单个矩阵。 您可以调用CGContextConcatCTM函数将CTM与仿射变换相结合。 仿射变换以及创建它们的函数将在Creating Affine Transforms中讨论。
实现累积效果的另一种方法是执行两次或更多次转换,而无需在转换调用之间恢复图形状态。 图5-6显示了使用以下代码行翻译图像然后旋转图像所产生的图像:
CGContextTranslateCTM (myContext, w,h);
CGContextRotateCTM (myContext, radians(-180.));
图5-7显示了使用以下代码行进行平移,缩放和旋转的图像:
执行多次转换的顺序很重要;如果您颠倒顺序,会得到不同的结果。 颠倒用于创建图5-7的转换顺序,您将得到如图5-8所示的结果,该结果由以下代码生成:
CGContextRotateCTM (myContext, radians ( 22.));
CGContextScaleCTM (myContext, .25, .5);
CGContextTranslateCTM (myContext, w/4, 0);
Creating Affine Transforms - 创建仿射变换
Quartz中可用的仿射变换函数在矩阵上运行,而不是在CTM上运行。 您可以使用这些函数构造一个矩阵,稍后通过调用CGContextConcatCTM函数将其应用于CTM。 仿射变换函数可以操作或返回CGAffineTransform数据结构。 您可以构造可重用的简单或复杂仿射变换。
仿射变换函数执行与CTM函数相同的操作 - 平移,旋转,缩放和连接。 表5-1列出了执行这些操作的功能及其使用信息。 请注意,每个平移,旋转和缩放操作都有两个函数。
Table 5-1 Affine transform functions for translation, rotation, and scaling
Quartz还提供了一个仿射变换函数,它可以反转矩阵CGAffineTransformInvert。反转通常用于提供变换对象内的点的逆变换。当您需要恢复已由矩阵转换的值时,反转非常有用:反转矩阵,并将值乘以反转矩阵,结果为原始值。您通常不需要反转变换,因为您可以通过保存和恢复图形状态来反转变换CTM的效果。
在某些情况下,您可能不希望转换整个空间,只需要转换点或大小。您通过调用函数CGPointApplyAffineTransform来操作CGPoint结构。您可以通过调用函数CGSizeApplyAffineTransform来操作CGSize结构。您可以通过调用函数CGRectApplyAffineTransform来操作CGRect结构。此函数返回包含传递给它的矩形的变换角点的最小矩形。如果对矩形进行操作的仿射变换仅执行缩放和平移操作,则返回的矩形与从四个变换角构造的矩形一致。
您可以通过调用函数CGAffineTransformMake来创建新的仿射变换,但与进行新仿射变换的其他函数不同,这个要求您提供矩阵条目。要有效地使用此功能,您需要了解矩阵数学。参见The Math Behind the Matrices。
Evaluating Affine Transforms - 评估仿射变换
您可以通过调用函数CGAffineTransformEqualToTransform来确定一个仿射变换是否等于另一个仿射变换。 如果传递给它的两个变换是相等的,则此函数返回true,否则返回false。
函数CGAffineTransformIsIdentity是用于检查变换是否是identity transform的有用函数。 identity transform不执行转换,缩放或旋转。 将此变换应用于输入坐标始终返回输入坐标。 Quartz常量CGAffineTransformIdentity表示identity transform。
Getting the User to Device Space Transform - 让用户进行设备空间转换
通常,当您使用Quartz 2D绘图时,您只能在用户空间中工作。 Quartz负责为您在用户和设备空间进行转换。如果您的应用程序需要获取Quartz用于在用户和设备空间之间进行转换的仿射变换,则可以调用函数CGContextGetUserSpaceToDeviceSpaceTransform。
Quartz提供了许多便利函数来转换用户空间和设备空间之间的几何。您可能会发现这些函数比应用函数CGContextGetUserSpaceToDeviceSpaceTransform返回的仿射变换更容易使用。
- 点 -
Points。函数CGContextConvertPointToDeviceSpace和CGContextConvertPointToUserSpace将CGPoint数据类型从一个空间转换为另一个空间。 - 大小 -
Sizes。函数CGContextConvertSizeToDeviceSpace和CGContextConvertSizeToUserSpace将CGSize数据类型从一个空间转换为另一个空间。 - 矩形 -
Rectangles。CGContextConvertRectToDeviceSpace和CGContextConvertRectToUserSpace函数将CGRect数据类型从一个空间转换为另一个空间。
The Math Behind the Matrices - 矩阵背后的数学
您需要了解矩阵数学的唯一Quartz 2D函数是CGAffineTransformMake函数,它通过3 x 3矩阵中的六个关键条目进行仿射变换。 即使您从未计划从头开始构造仿射变换矩阵,您也可能会发现变换函数背后的数学很有趣。 如果没有,您可以跳过本章的其余部分。
3 x 3变换矩阵-a,b,c,d,tx和ty-的六个关键值显示在以下矩阵中:
注意:矩阵最右边的列始终包含常量值0,0,1。在数学上,需要第三列以允许连接,本节稍后将对此进行说明。 出于数学正确性的目的,它出现在本节中。
给定上述3 x 3变换矩阵,Quartz使用此公式将点(x,y)变换为结果点(x',y'):
结果在不同的坐标系中,由变换矩阵中的变量值转换。 以下等式是前一个矩阵变换的定义:
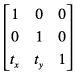
以下矩阵是单位矩阵。 它不执行转换,缩放或旋转。 将此矩阵乘以输入坐标始终返回输入坐标。
使用前面讨论的公式,您可以看到此矩阵将生成一个与旧点(x,y)相同的新点(x',y'):
他的矩阵描述了translation操作:
这些是Quartz用于应用translation的结果公式:
该矩阵描述了对点(x,y)的缩放操作:
这些是Quartz用于缩放坐标的结果公式:
该矩阵描述了旋转操作,将点(x,y)逆时针旋转角度a:
这些是Quartz用于应用旋转的结果公式:
此等式将旋转操作与转换操作连接在一起:
这些是Quartz用于应用变换的结果公式:
请注意,连接矩阵的顺序很重要 - 矩阵乘法不是可交换的。也就是说,矩阵A乘以矩阵B的结果不一定等于矩阵B乘以矩阵A的结果。
如前所述,连接是仿射变换矩阵包含具有常数值0,0,1的第三列的原因。为了将一个矩阵与另一个矩阵相乘,一个矩阵的列数必须与另一个矩阵的行数相匹配。 这意味着2 x 3矩阵不能与2 x 3矩阵相乘。因此,我们需要包含常量值的额外列。
反演操作(inversion operation)从转换后的坐标生成原始坐标。给定坐标(x,y),其已经由给定矩阵A变换为新坐标(x',y'),将坐标(x',y')由A的逆矩阵产生原始坐标( x,y)。当矩阵乘以其逆矩阵时,结果是单位矩阵。
后记
本篇主要讲述了变换,感兴趣的给个赞或者关注~~~